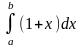Экзаменационный вопрос № 29. Алгоритмы нахождения корней уравнений

1. Метод половинного деления. Суть метода заключается в последовательном делении отрезков пополам, где находится точка корня уравнения. Обобщенная формула:

2. Метод хорд состоит в том, что на выделенном интервале [a; b] нелинейная функция f(x) заменяется линейной, в качестве которой берется хорда — прямая, стягивающая концы нелинейной функции. Обобщенная формула:

- 16 -

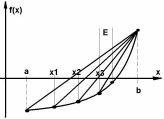
3. Метод Ньютона (касательных) заключается в том, что на выделенном интервале [a; b] нелинейная функция f(x) заменяется касательной, проводимой в текущей точке последовательности. Обобщенная формула:

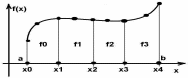
4. Метод прямоугольников состоит в том, что подынтегральная функция приближенно заменяется более простой горизонтальной прямой, при этом получается прямоугольники, сумму площадей которых мы и находим:

Обобщенная формула:

Экзаменационный вопрос № 30. Алгоритмы численного интегрирования

5. Метод трапеций заключается в том, что подынтегральная функция приближенно заменяется более простой наклонной прямой, при этом получаются трапеции, сумму площадей которых необходимо найти:

Обобщенная формула:

6. Метод Симпсона состоит в том, что подынтегральная функция заменяется квадратичной параболой, которая строится по трем точкам на каждом участке. По этим точкам (крайним точкам участка и средней точке) строится интерполяционная функция — полином второго порядка, который аналитически интегрируется.

Обобщенная формула:

Экзаменационный вопрос № 31. Программа вычисления определенного интеграла методом прямоугольников

Задание. Используя подпрограмму-процедуру, составить программу для вычисления определенного интеграла, указанным численным методом. Определить число итераций, необходимых для вычисления суммы.

Исходные данные.

№п/п	Определенный интеграл	Метод	a	b	Точность вычислений	Ответ	Число итераций
1		Прямо- угольников	(10 div 2 –1)/4 – – 1	3 (10 mod3)4– –3 sqr(2) + 1	10–3	1,499	10

Код программы.

Program primer1;

uses crt;

Var

int: real;

iter: integer;

{int — значение вычисляемого интеграла}

{iter — количество итераций}

Const

eps =0.001; {точность вычислений}

a= trunc((10 div 2–1)/4–1);

{a —-левая граница отрезка интегрирования}

{div — операция целочисленного деления} {trunk превращает значение вещественного типа в целочисленное путем

отбрасывания дробной части}

b=trunc(3*(10 mod 3)*4–3*sqr(2)+1);

{b — правая граница отрезка интегрирования}

{mod — операция остатка от целочисленного деления}

Function Y(x:real) : real;

begin

Y:=1+x; {вычисление функции в точке}

end;

Procedure Metod_pryam( a, b : integer; eps: real);

var j : integer;

h, sum,i1,i2,y:real;

{h — шаг интегрирования} {sum — переменная для суммирования значений функции}

{I1 — первое приближенное значение интеграла}

{I2 — второе приближенное значение интеграла}

{j — индекс прохождения по отрезку шагом разбиения h}

begin

i2:=0; {Задание начального значения определенного интеграла}

iter :=0; {Инициализация переменной для подсчета количества итераций}

h:=(b–a)/10;

repeat

i1:=i2; {Нахождение нового приближенного значения интеграла}

sum:=0; {Обнуление значения суммы}

for j:=1 to trunc((b–a)/h)–1 do

{цикл по всему отрезку интегрирования шагом интегрирования}

begin

sum:=sum+Y(a+j*h);

{Вызов и выполнение процедуры, где находим значение функции Y, cуммирование функций и нового значения функции в заданной точке}

end;

sum:=sum+a;

{Добавление к сумме функций значения левой границы отрезка}

i2:=sum*h;

{Нахождение новой приближенной величины определенного

интеграла}

h:=h/2 {Уменьшение шага разбиения в 2 раза}

iter:=iter+1 ; {Происходит увеличение числа итераций}

until abs(i1–i2)<=eps;

{abs(I1–I2)<=eps — проверка точности достижения результата}

{Если abs(I1–I2) оказалось <=eps, то цикл завершается}

{Если abs(I1–I2) оказалось >eps, то цикл проводит еще одну итерацию}

int:=i2;

{глобальной переменной присваивается значение локальной, равной значению интеграла}

end;

begin

clrscr; {clrsc r— метод из модуля CRT, осуществляющий очистку экрана}

writeln(‘a=’,a);

writeln(‘b=’,b);

Metod_pryam(a,b,eps);

{вызов процедуры, вычисляющей определенный интеграл}

writeln('Ответ: I=',int:5:3);

writeln(‘Кол-во итераций: i=’,iter);

write(‘Нажмите ENTER’); {Вывод сообщения на экран}

readln();

end;