3. Подбор сечений стержней фермы.

Данные:

• коэффициент условий работы _c=0,95;

• материал конструкций фермы – сталь С245;

• толщина фасонки t до 20 мм;

• по табл. 51 СНиП II-23-81*: расчетное сопротивление стали растяжению, сжатию, изгибу по пределу текучести EMBED Equation.3 .

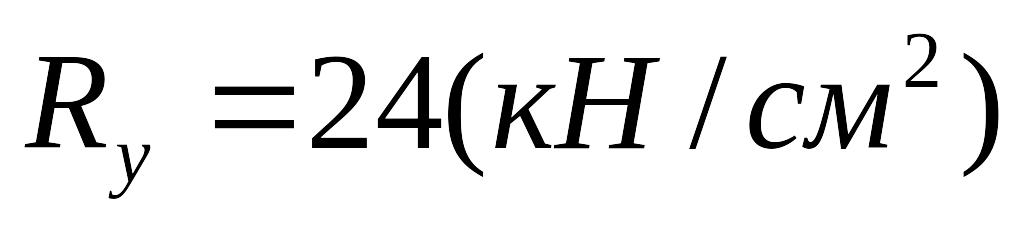1. Подбор сечений стержней верхнего пояса фермы. Элементы в1 – 1, в2 – 3, в3 – 4.

Расчетное усилие: EMBED Equation.3 ;

Расчетные длины стержня: EMBED Equation.3 ; EMBED Equation.3 .

Поскольку l_x = l_у, принимаем тавровое сечение из двух равнополочных уголков, зададимся гибкостью в пределах рекомендуемых для поясов легких ферм: EMBED Equation.3 , тогда условная гибкость:

EMBED Equation.3 .

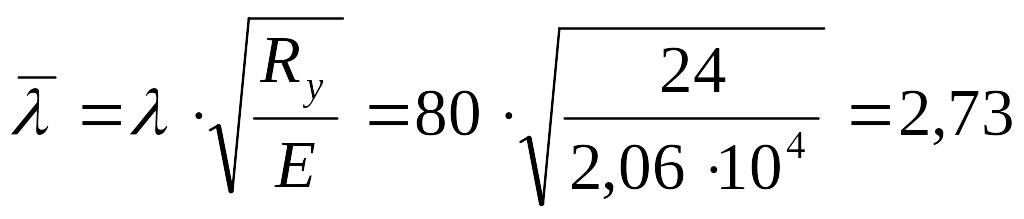По табл. 72 СНиПа II-23-81* находим,  = 0,686.

• Требуемая пло­щадь поперечного сечения:

EMBED Equation.3 .

Принимаем сечение из двух равнополочных уголков 20014:

Размеры, мм					Площадь сечения, см2	Справочные величины для осей						Радиус инерции составного сечения при расстоянии t1, мм				Масса 1 м, кг
						x – x		xo – xo		yo – yo
b	t	R	r	zo		Ix, см4	ix, см	Ixo, см4	ixo, см	Iyo, см4	iyo, см	10	12	14	16
200	14	18	6	54,6	54,6	2097	6,2	3333	7,81	861	3,97	8,6	8,67	8,74	8,81	42,8

Принимаем толщину фасонки 12 мм.

• Расчетные гибкости стержня в плоскостях, перпендикулярных осям х–х и у–у:

EMBED Equation.3 ;

EMBED Equation.3 .

• Условную гибкость, определяемая по максимальной гибкости (перпендикулярной осям х–х):

EMBED Equation.3 .

По табл. 72 СНиПа II-23-81* находим,  = 0,859.

• Проверка несущей способности подобранного сечения:

EMBED Equation.3 .

Получили большое недонапряжение, поэтому изменим уже подобранное сечение, задав гибкость EMBED Equation.3 , тогда условная гибкость:

EMBED Equation.3 .

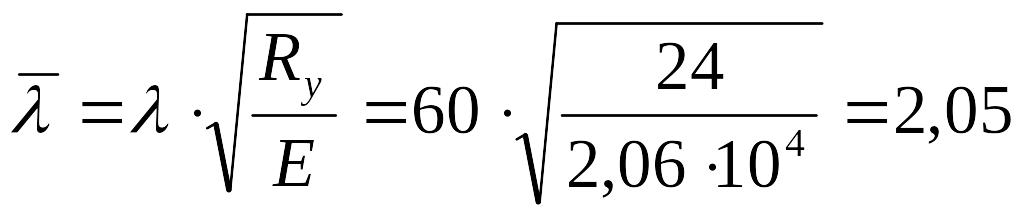По табл. 72 СНиПа II-23-81* находим,  = 0,805.

• Требуемая пло­щадь поперечного сечения:

EMBED Equation.3 .

Принимаем сечение из двух равнополочных уголков 20012:

Размеры, мм					Площадь сечения, см2	Справочные величины для осей						Радиус инерции составного сечения при расстоянии t1, мм				Масса 1 м, кг
						x – x		xo – xo		yo – yo
b	t	R	r	zo		Ix, см4	ix, см	Ixo, см4	ixo, см	Iyo, см4	iyo, см	10	12	14	16
200	12	18	6	53,7	47,1	1823	6,22	2896	7,84	749	3,99	8,5	8,62	8,69	8,76	37

Принимаем толщину фасонки 12 мм.

• Расчетные гибкости стержня в плоскостях, перпендикулярных осям х–х и у–у:

EMBED Equation.3 ;

EMBED Equation.3 .

• Условную гибкость, определяемая по максимальной гибкости (перпендикулярной осям х–х):

EMBED Equation.3 .

По табл. 72 СНиПа II-23-81* находим,  = 0,859.

• Проверка по несущей способности подобранного сечения:

EMBED Equation.3 .

• Проверка по предельной гибкости элемента.

Из табл. 19 СНиПа II-23-81* предельная гибкость равна:

EMBED Equation.3 ,

где EMBED Equation.3 , тогда

EMBED Equation.3

Т.е. подобранное сечение удовлетворяет условию:

EMBED Equation.3 .

Окончательно для элементов В₁ – 1, В₂ – 3, В₃ – 4 принимаем сечение из двух уголков 20012.