1.5 Алгоритмы для исполнителей

Третий тип модели алгоритма основывается на так называемых алгоритмах для исполнителей. Его абстрактной реализацией выбирают часто машину Тьюринга. Она связывает понятие алгоритма с механическим устройством, способным выполнять строго фиксированное множество элементарных действий над простейшими символами;

Машина Тьюринга (МТ) - это абстрактная машина (автомат), работающая с лентой отдельных ячеек, в которых записаны символы. Машина также имеет головку для записи и чтения символов из ячеек, которая может двигаться вдоль ленты. На каждом шагу машина считывает символ из ячейки, на которую указывает головка, и, на основе считанного символа и внутреннего состояния, делает следующий шаг. При этом, машина может изменить свое состояние, записать другой символ в ячейку или передвинуть головку на одну ячейку вправо или влево. Подробно МТ будет рассмотрена в следующей главе. Здесь напомним частные её реализации в виде машины Поста и автоматов (конечных, магазинных и других).

В 1936 г. Эмиль Леон Пост (Emil L. Post) опубликовал статью «Финитные комбинаторные процессы — формулировка 1», в которой было дано одно из первых уточнений понятия алгоритма. Им была предложена конструкция в виде абстрактной машины, которая выполняла очень простые операции, имитирующие действия человека. Пост сам был удивлен тем, что машина могла вычислять очень сложные функции, если их удавалось изложить на «языке» машины. Конструкция Поста положила начало целому «машинному ряду» уточнений алгоритма, насчитывающему к настоящему времени около сотни абстрактных машин.

1. Конструкция машины Поста. Машина Поста содержит следующие составные части (смотри рисунок. 3.2):

а) бесконечную входную ленту, разделенную на клетки, которая служит для записи информации; каждая клетка может быть в двух состояниях: ◊ — пустая, * — записан символ «*» (иногда используют другие символы);

б) головку считывания/записи (Г), которая может передвигаться вдоль ленты на одну клетку влево или вправо, стирать клетку (ставить ◊), записывать символ «*».

2. Работа машины. Работа машины состоит в том, что головка передвигается вдоль ленты и записывает или стирает символы. Работа производится по инструкции — программе, состоящей из отдельных команд.

3. Команды машины. Формат команд приведен в таблице 1.

4. Процесс выполнения. Он начинается с первой команды программы, на каждом шаге производится действие и переход к команде, которая должна выполняться следующей.

Текущее состояние машины Поста описывается состоянием ленты и положением каретки. Состояние ленты – информация о том, какие секции пусты, а какие отмечены. Шаг – это движение каретки на одну ячейку влево или вправо. Состояние ленты может изменяться в процессе выполнения программы. Входные данные записываются на ленте, результат получается на ленте при останове машины. У команды «стоп» отсылки нет.

Варианты окончания выполнения программы на машине Поста:

Команда "стоп" - корректная остановка. Возникает в результате выполнения правильно написанного алгоритма.

Выполнение недопустимой команды – нерезультативная остановка. Случаи, когда головка должна записать метку там, где она уже есть, или стереть метку там, где ее нет, являются аварийными (недопустимыми).

Уход в бесконечность, зацикливание. Машина Поста в результате работы алгоритма может вообще не остановиться (никогда не дойти до команды «стоп» и никогда не завершиться аварийной ситуацией).

Элементарные действия (команды) машина Поста проще команд машины Тьюринга. Поэтому программы для машины Поста имеют большее число команд, чем аналогичные программы для машины Тьюринга. Почему достаточно лишь два различных символа (есть метка, нет метки)? Дело в том, что любой алфавит может быть закодирован двумя знаками; в зависимости от алфавита возрастать может только количество двоичных символов в букве алфавита.

Машина Поста является прародителем всех процедурных языков программирования.

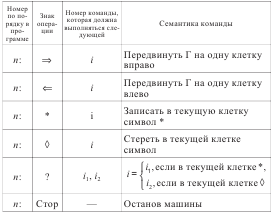
Таблица 1.

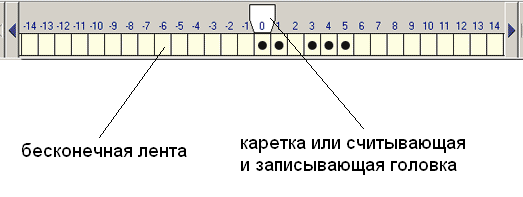
Рисунок 3.2

Как было указано ранее, реализация распознающей грамматики находит свое воплощение в автоматах, которые входят в рассматриваемый тип алгоритмической модели. Так конечный автомат (КА) может решать следующую задачу. Пусть задан алфавит A={,a,b,*}и пусть задано отношение L— множество слов вида ambn *для m,n=1,2,...то есть L={ ambn *} Пусть x— произвольное слово в A. Надо построить функцию (предикат) такую, что f(x) =1 или 0, если x или ∉ L. Здесь символ «*» — признак конца слова. Построим следующий «механизм» или КА:

Механизм может находиться в некоторых состояниях S_y, в том числе: начальное — S_s и конечные — S_e , при получении на входе какого-либо символа механизм переходит в другое состояние и, если оно не конечное S_e, то он может воспринимать следующий символ. Записывают конечный автомат в виде команды, графа или таблицы.

Рассматривается еще одна автоматная конструкция —так называемый магазинный (стековый) автомат (МА). У МА имеется:

1. Входная лента E, разделенная на ячейки и потенциально неограниченная в обе стороны.

2. Рабочая лента (лента магазинной памяти, или стек) M, также разделенная на ячейки и ограниченная с одной стороны (например, слева), но потенциально неограниченная с другой.

3. Управляющее устройство A с двумя головками:

— входная головка (головка чтения), читающая символы на входной ленте E;

— рабочая головка, читающая, стирающая и записывающая символы на рабочей ленте M.

Каждая головка может передвигать свою ленту по определенным правилам, которые будут уточнены.

Входная лента. До начала работы МА на входной ленте записана некоторая информация — по одному символу в каждой ячейке. Для записи ее используется входной словарь (входной алфавит):

V E ={a₁,a₂,...,a_p}. Цепочки (слова), составленные из символов входного алфавита, записываются на ленте E слева направо так, что слова и справа остаются пробелы, обозначаемые символом B.

Рабочая лента. Запись на рабочей ленте производится самим автоматом с помощью рабочего словаря (рабочего алфавита):

VM={ А₁,A₂,..., A_q}. Алфавит VM может включать в себя и алфавит AE. Изначально в самой левой ячейке записан специальный символ ◊ — «доннышко».

Управляющее устройство. Управляющее устройство способно принимать конечное число внутренних состояний S₀,S₁,...,S_n, то есть задан алфавит внутренних состояний:

VS={ S₀,S₁,...,S_n}. Первое из них (S₀)считается начальным, последнее (S_n) — конечным.

Функционирование МА. В каждый момент времени МА находится в некоторой ситуации, которая описывается тройкой:

< a_I, S_j, A_k,>, где a_i—символ, записанный на ленте E и обозреваемый в данный момент входной головкой, S_j — внутренее состояние управляющего устройства, A_k—символ, записанный на ленте M и обозреваемый в данный момент рабочей головкой.

Командой МА называется запись вида: <ситуация>→< S_m,x>, где ситуация определена выше, S_m - внутренее состояние, x—действие с рабочей лентой.

Абстрактным МА называется конечное множество команд указанного вида.