3.1. Нумерация алгоритмов

Нумерация алгоритмов играет важную роль в их исследовании и анализе. Поскольку любой алгоритм можно задать в виде конечного слова (представить в виде конечной последовательности символов некоторого алфавита), а множество всех конечных слов в конечном алфавите счётное, то множество всех алгоритмов также счётное. Это означает существование взаимно однозначного отображения между множеством натуральных чисел и множеством алгоритмов, то есть возможность присвоить каждому алгоритму номер.

Нумерация алгоритмов является одновременно и нумерацией всех алгоритмически исчисляемых функций, причем любая функция может иметь бесконечное количество номеров.

Существование нумерации позволяет работать с алгоритмами так же, как с числами. Особенно полезна нумерация в исследовании алгоритмов, работающих с другими алгоритмами.

Пусть имеется некая массовая проблема с множеством исходных объектов X и множеством искомых объектов Y. Для существования решения массовой проблемы необходимо, чтобы элементы множеств X и Y были конструктивными объектами. Следовательно, элементы этих множеств можно занумеровать натуральными числам. Пусть x∈ X – некий исходный объект, обозначим через n(x) его номер. Если в массовой проблеме по исходному объекту x требуется получить искомый объект y∈Y с номером n(y), то определим арифметическую функцию f: Nn→N, такую что f(n(x))=n(y).

В качестве примера построения арифметических функций по массовым проблемам рассмотрим массовые проблемы.

1. Если дан массив [x1, x2, …, xn] натуральных чисел, то ему в соответствие можно поставить натуральное число 2x1, 3x2,... p(n)xn , где p(n) – n-е простое число. Рассмотрим для примера массив длины 5:

[x1, x2, x3, x4, x5] 2x13x25x37x411x5.

Данная нумерация определяет арифметическую функцию f (например, f(73500) = f(22315372110) = 20315272113 = 4891425).

2. Любое рациональное число имеет некоторый натуральный номер. Нумерация множества искомых объектов проблемы тривиальна:

{«да», «нет»} a {1, 0}. Для данной массовой проблемы можно построить арифметическую функцию одного аргумента, воспользовавшись приемом из предыдущего примера, а можно рассмотреть функцию трех аргументов (три номера элементов исходной тройки).

3. Нумерация текстов программ может быть осуществлена следующим образом: любую программу можно воспринимать как запись числа в 256-ричной системе счисления (если для записи программы использовались символы таблицы ASCII).

Переход от массовой проблемы к арифметической функции позволяет свести вопрос о существовании решения массовой проблемы к вопросу существования эффективного способа вычислений значений арифметической функции по ее аргументу (аргументам).

3.2 Нумерация наборов чисел

В теории алгоритмов получил распространение прием, позволяющий сводить изучение функций от нескольких переменных к изучению функций одной переменной. Он основан на нумерации наборов чисел так, что имеется биективное соответствие между наборами чисел и их номерами, причем функции, определяющие по набору чисел его номер и по номеру сам набор чисел являются общерекурсивными. Например, для функции, содержащей две независимых переменных (x, y), это отображение h(x, y) может быть таким:

Рисунок 1.

Пусть пары (x, y) формируют частично упорядоченное множество N⁽²⁾. Если дано h(x, y) = n, то существует обратное отображение: x = h^-1₁(n) и y= h^-1₂ (n), т. е. h(h^-1₁ (n), h^-1₂ (n) ) = n. Это позволяет вычислять номер n для любой пары (x, y) и, наоборот, по номеру n вычислять значения x и y:

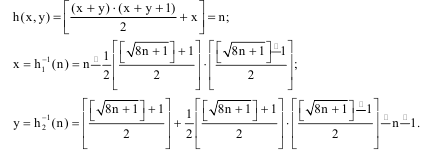
Используя эти правила, можно вычислять нумерацию троек h²(x, y, z) = h(h(x, y), z) = n и, наоборот, по номеру тройки - значения x, y, z. Например, если h² (x, y, z) = n, то z= h^-1₂(n), y= h^-1₂ (h^-1₁ (n)), x= h^-1₁ (h^-1₁ (n)), h²(x, y, z) = h(h(h^-1₁ (h^-1₁ (n)), h^-1₂ (h^-1₁ (n))), h^-1₂ (n)). Тройки (x, y, z) формируют частично упорядоченное множество N⁽³⁾. Аналогично для произвольного количества чисел имеем:

h^n-1(x1, x2,…, xn)=h(h…h(h(x1, x2), x3)…x_n-1), xn). Если h^n-1(x1, x2,…, xn)=m, то xn= h^-1₂ (m), x_n-1 =h^-1₂ (h^-1₁ (m)), ....................................., x2= h^-1₂ (h^-1₁ (...h^-1₁ (m)...)), x1= h^-1₂ (h (...h (m)...)).

Имея нумерацию множеств наборов N⁽¹⁾, N⁽²⁾,..., N ⁽ⁱ⁾,..., N(ⁿ, где N ⁽ⁱ⁾ – множество наборов (i) чисел, можно установить объединенную нумерацию произвольных наборов чисел M = N⁽¹⁾ N⁽²⁾ ... N ⁽ⁱ⁾ .. N(ⁿ⁾, где M N. Для любого n N имеем h(x1,x2,..., xn )= h(hⁿ⁻¹(x1,x2,..., xn ), n −1).

Если h(x ,1x ,2..., x )n= m, то hⁿ⁻¹(x ,1x ,2..., x )n= h^-1₁ (m), n= h^-1₂ (m)+1. Используя вышеприведенные формулы, можно восстановить значения x1, x2,…, xn.