2.4 Варианты машины Тьюринга

Модель машины Тьюринга допускает расширения. Можно рассматривать машины Тьюринга с произвольным числом лент и многомерными лентами с различными ограничениями. Однако все эти машины являются полными по Тьюрингу и моделируются обычной машиной Тьюринга.

В качестве примера такой эквивалентности рассмотрим сведение любой МТ к МТ, работающая на полубесконечной ленте.

Теорема: Для любой машины Тьюринга существует эквивалентная машина Тьюринга, работающая на полубесконечной ленте.

Доказательство:

Рассмотрим доказательство Ю. Г. Карпова. Доказательство этой теоремы конструктивное, то есть мы дадим алгоритм, по которому для любой машины Тьюринга может быть построена эквивалентная машина Тьюринга с объявленным свойством. Во-первых произвольно занумеруем ячейки рабочей ленты МТ, то есть определим новое расположение информации на ленте:

Рисунок 1.

Затем перенумеруем ячейки, причём будем считать, что символ «*» не содержится в словаре МТ:

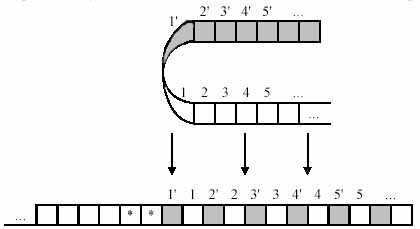
Рисунок 1.

2.5 Вычислимость по Тьюрингу и разрешимость

Выше было доказано, что классы функций, вычислимых с помощью рекурсивных функций, машин Тьюринга или нормальных алгоритмов Маркова, совпадают. Это позволяет рассматривать понятие «вычислительный алгоритм» инвариантным к способу описания. Различия наблюдаются лишь в использовании алгоритмических объектов. Если для рекурсивных функций объектами являются числа и числовые функции, а процесс вычисления задан операторами суперпозиции, рекурсии, минимизации и итерации, то для машин Тьюринга такими объектами являются символы алфавитов внешней и внутренней памяти, а процесс вычисления задан протоколом, использующим функции выхода, перехода и перемещения головки. Для нормального алгоритма Маркова такими объектами являются слова или последовательности символов, а процесс вычисления задан правилами подстановки или продукциями, изменяющими состав и структуру исходной последовательности символов до искомого результата.

Арифметической (числовой) функцией называют функцию, областью значений которой является подмножество множества N, а областью определения - элемент множества N.

Для алгоритмических проблем типичной является ситуация, когда требуется найти алгоритм для вычисления числовой функции f(x₁ , x₂ , …, x_n ), зависящей от целочисленных значений аргументов x₁ , x₂ , …, x_n .

Функцию f:N_n→N назовем вычислимой, если существует алгоритм, позволяющий для любого набора значений ее аргументов вычислить значение функции (или указать, что функция на данном наборе не определена). Так как в определении вычислимой функции используется интуитивное понятие алгоритма, то часто вместо термина «вычислимая функция» используется термин «интуитивно вычислимая функция». Таким образом, массовая проблема имеет решение, если арифметическая функция, соответствующая этой проблеме, является интуитивно вычислимой.

Функция f(x₁, x₂ , …, x_n) называется эффективно вычислимой, если для заданных значений k₁, k₂, …, k_n  аргументов можно найти значение функции        f(k₁, k₂, …,k_n) с помощью некоторой  имеющейся  механической процедуры (алгоритма).

Вместо уточнения понятия алгоритма можно рассматривать уточнение понятия «вычислимая функция». Обычно при этом действуют по следующей схеме:

1. Вводят точно определенный класс функций.

2. Убеждаются, что все функции из этого класса являются вычислимыми.

3. Принимают гипотезу (тезис) о том, что класс вычислимых функций совпадает с введенным классом функций.

Функция называется вычислимой, если существует вычисляющий её алгоритм. «Вычислимость» является одним из основных понятий теории алгоритмов, инвариантном к вычисляемой функции и алгоритму. Различие между вычислимой функцией и алгоритмом – это различие между описанием функции и способом вычисления её значений при заданных значениях независимых аргументов.

Тезис Тьюринга. Всякий интуитивный алгоритм может быть реализован с помощью некоторой машины Тьюринга.

Из тезиса Тьюринга следует, что, если возникают алгоритмические проблемы, то их следует решать на базе построения машин Тьюринга, то есть достаточно формализованного понятия алгоритма. При этом в алгоритмических проблемах часто речь идет не о построении алгоритма, а о вычислимости некоторых специальным образом построенных функций.

Следует отметить, что в этих случаях достаточно использовать алфавит {0,|}, где 0 – пустой символ. Например, натуральные числа, включая 0, в этом алфавите кодируются следующим образом: 0 - |; 1 - ||; 2 - |||; 3 -|||| ; …. ; n - ||…| (n + 1 раз).

Частичная числовая n – местная функция f(x1 , x2 , …, xn) называется вычислимой по Тьюрингу, если существует машина М, вычисляющая ее в следующем смысле:

1. Если набор значений аргументов  <x1 , x2 , …, xn>  принадлежит области определения функции  f , то машина М, начиная работу в конфигурации

0 |^x1+1 0 |^x2+1 … 0 |x_n q₁|, где   |x  =  ||… |  (x раз)

,и воспринимается самый правый символ, останавливается, заканчивая работу в конфигурации  0|^yq₀|, где y = f(x₁ , x₂ , …, x_n).

2. Если набор значений аргументов <x₁ , x₂ , …, x_n>  не принадлежит области определения функции f , то машина М, начиная работу в исходной конфигурации, работает бесконечно, то есть не приходит в заключительное состояние.

Машина Тьюринга есть точное формальное определение  алгоритма. С помощью этого понятия можно доказывать разрешимость или неразрешимость алгоритмических проблем.

Если для решения задачи, принадлежащей единому классу задач, найден алгоритм вычисления, то о задаче говорят как об алгоритмически разрешимой проблеме. Иначе говоря, обязательным условием вычислимости или результативности вычисления является её алгоритмическая разрешимость. В этом смысле понятие «разрешимость» является также основным понятием в теории алгоритмов.

Анализ трех типов моделей показывает, что основные свойства дискретности, детерминизма, массовости и результативности остаются неизменными для различных способов описания:

• Свойство дискретности: алгоритм состоит из отдельных элементарных действий, выполняемых по шагам; множество элементарных шагов, из которых состоит алгоритмический процесс, конечно и счетно.

• Свойство детерминированности: после каждого шага дается точное указание, как и в какой последовательности выполнять следующие шаги алгоритмического процесса.

• Свойство массовости: использование алгоритма допустимо для множества алгоритмических объектов данного типа и данного класса задач.

• Свойство результативности: остановка алгоритмического процесса обязательна после конечного числа шагов с указанием искомого результата.

Однако, тезис невозможно доказать, так как он связан точным понятием вычислимости по Тьюрингу с неточным понятием интуитивно вычислимой функции.