
- •15.Коррозия арматуры.
- •Проф.Алексеев предложил различать три вида коррозии арматуры:
- •16. Железобетон
- •17.Методы расчета ж/б по допускаемым напряжениям и по разрушающим нагрузкам.
- •18.Метод расчёта по предельным состояниям
- •20. Величины предварительного напряжения
- •21. Стадии напряжённо деформированного состояния при изгибе (ндс)
- •22. Преднапряжённые элементы
- •23. Граничная высота сжатой зоны бетона
- •24. Расчёт изгибаемых элементов прямоугольного сечения с одиночной а
- •25. Расчёт изгибаемых элементов прямоугольного сечения с двойной арматурой
- •26. Расчёт тавровых и двутавровых сечений
- •27. Второй случай расчёта
- •28. Расчёт железобетонных элементов по наклонному сечению
- •29. Расчет ж/б элементов по полосе между наклонными трещинами.
- •30. Расчёт железобетонных элементов по наклонным сечениям на действие поперечных сил
- •31. Расчёт железобетонных элементов по наклонным сечениям на действие моментов
- •32. Расчёт сжатых элементов
- •33. Внецентренно сжатые элементы
- •34. Расчёт элементов на местное сжатие
- •35. Расчёт железобетонных элементов по образованию трещин
- •36. Расчёт по образованию трещин в изгибаемых элементах
- •37. Расчёт Железобетонных элементов по раскрытию трещин
- •38. Расчёт железобетонных элементов по деформациям
- •40.Определение полной кривизны изгибаемых элементов с трещинами в растянутой зоне.
- •41. Конструктивные схемы гражданских зданий
- •42. Рамный каркас многоэтажных зданий
- •43. Здания из монолитного железобетона
- •44. Одноэтажные промышленные здания
- •47. Расчёт внецентренно сжатых элементов
- •46. Расчёт элементов неармированной кладки при центральном сжатии
- •45. Общие сведения о каменных конструкциях. Прочность каменной кладки при сжатии
- •53. Расчет стен подвала.
- •52. Расчет карнизных участков стен.
- •51. Статический расчёт каменных зданий с жесткой конструктивной схемой.
- •50. Элементы с продольным армированием
- •49. Расчет элементов каменных конструкций с сетчатым а.
- •48. Расчёт каменных конструкций на местное сжатие (смятие)
26. Расчёт тавровых и двутавровых сечений
Общие сведения
В стр-ве применяются изг элементы, имеющие форму тавра или двутавра с полкой в сжатой зоне. Это балки покрытия, пустотные плиты перекрытия, ребристые плиты перекрытия, балки монолитных перекрытий, подкрановые балки, ригели перекрытий.

Расчёт сечений, имеющих полку в сжатой зоне, производится в зависимости от положения нейтральной оси. Встречаются два случая расчёта.
Первый случай расчёта
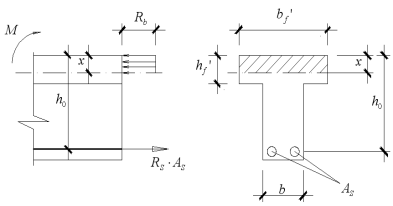
Этот случай встречается тогда, когда нейтральная ось проходит в полке, т.е. соблюдается условие: Mf ≥ М, (1) Rb b hf ’ ≥Rs As (2)
Mf - момент, воспринимаемый полкой относительно центра тяжести растянутой арматуры; М – момент от внешней нагрузки относительно центра тяжести растянутой арматуры; Mf = bf ’ hf ’ Rb (h0 – 0.5 hf’), где (3)
bf ’ – ширина полки вводимая в расчёт, принимаемая по п.3.26 (Пособие);
hf ’ – толщина полки. Если условие (1) или (2) выполняется, то нейтральная ось проходит в полке и сечение рассчитывается как прямоугольное шириной равной bf ’
Условие равновесия Rs As = Rb ξ bf ’ h0 (4)
M = αm Rb bf ’ h0 2 (5); αm = M / Rb bf ’ h0 2 ; (6)
ξ определяем через αm (1 - √(1 - 2 αm )
Площадь сечения рабочей растянутой арматуры определяется по формуле:
As = Rb bf ’ h0 ξ / Rs ; (7)
П орядок
расчета
орядок
расчета
Определить As
h0
проверяется условие (1)
αm = M / Rb bf ’ h0 2 ;
As = Rb bf ’ h0 ξ / Rs ;
Определить Мu
h0
проверяется условие (2)
ξ =Rs*As/Rb* bf ’*h0
x =ξ h0
Мu =Rb bf ’x (h0 – 0.5x),
M ≤ Мu
27. Второй случай расчёта
Этот случай встречается тогда, когда нейтральная ось проходит в ребре, т.е. соблюдается условие:Mf ≤ М; (1) Rb bf ’ hf ’<Rs As

Сжатая зона бетона разделяется на две части: сжатое ребро и сжатые свесы полок. Тогда условия равновесия можно записать следующим образом: Rbb x + A0ν Rb = Rs As ,
где A0ν – площадь свесов полки, равная (bf ’ – b) hf ’
M = αm Rbbh0 2 + A0ν Rb (h0 – 0.5 hf’);
Площадь сечения растянутой арматуры определяется по формуле: As = [Rb b h0(1 - √(1 - 2 αm ) - A0ν Rb ]/ Rs ,
где αm = [М - A0ν Rb (h0 – 0.5 hf’)]/ Rbbh0 2 .
При этом должно соблюдаться условие αm ≤ αR.
порядок расчета
h0
проверяется условие (1)
αm = [М - A0ν Rb (h0 – 0.5 hf’)]/ Rbbh0 2 .
ξ
As = [Rb b h0(1 - √(1 - 2 αm ) - A0ν Rb ]/ Rs
28. Расчёт железобетонных элементов по наклонному сечению
Общие положения расчёта
Вблизи опор от действия момента и поперечной силы возникают наклонные трещины. После образования трещин элемент разделяется на 2 части, соединённые в верхней части сжатой зоной бетона, а в нижней – продольной и поперечной арматурой.
Разрушение элемента происходит по 3 случаям.
С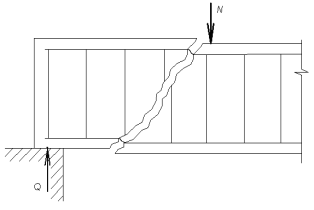
 лучай
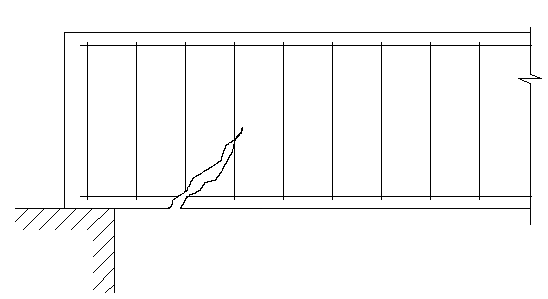
1-й. Происходит
в тавровых и двутавровых элементах при
малой ширине стенки. Разрушение происходит
между наклонными трещинами от действия
поперечной силы от дробления Б стенки
от главных напряжений
лучай
1-й. Происходит
в тавровых и двутавровых элементах при
малой ширине стенки. Разрушение происходит
между наклонными трещинами от действия
поперечной силы от дробления Б стенки
от главных напряжений
Случай 2- й. Сечение продольной А достаточно и обеспечена её надёжная анкеровка, что препятствует повороту обеих частей элемента. Разрушение по наклонному сечению происходит после достижения предельных значений в поперечной А из-за среза Б над наклонной трещиной (рис. 20б). Обе части элемента смещаются друг относительно друга. Такое разрушение вызывается действием поперечной силой.
Случай 3-й. От действия момента поворачиваются части элемента относительно центра тяжести сжатой зоны Б над трещиной. При этом трещина раскрывается, развивается по высоте, сокращается сжатая зона Б. Напряжения в Б достигают редельных и происходит разрушение элемента. Может произойти разрушение от проскальзывания А (рис. 20а).
