22. Преднапряжённые элементы

Стадии напряжённо-деформированного состояния (НДС) при изгибе преднапряжённых элементов.

Стадия изготовления

В исходном состоянии преднапряжённого элемента до приложения нагрузки в верхней зоне бетона возникают растягивающие напряжения, а в нижней зоне – сжимающие напряжения. В предварительно напряжённой арматуре - напряжения за вычетом всех потерь.

СтадияI

В стадии I, которая соответствует нагрузкам стадии обычного элемента, в бетоне нижней зоны не возникают растягивающие напряжения. Происходит только погашение обжатия бетона. Стадия I_a наступает при нагрузках, превышающих нагрузки стадии I_a обычных элементов. Таким образом, трещины в преднапряженных элементах образуются при более высоких нагрузках, чем в обычных элементах. Предварительное напряжение повышает трещиностойкость изгибаемых элементов.

Стадия II

С дальнейшим ростом нагрузки трещины в растянутой зоне раскрываются. Однако, ширина их раскрытия меньше, чем во второй стадии обычных элементов. Прогибы изгибаемых преднапряжённых элементов за счёт обратного выгиба также меньше, чем в обычных элементах.

По стадии два рассчитывают прогибы и ширину раскрытия трещин.

Стадия III

В этой стадии преднапряжённые элементы работаю, как обычные элементы. Наблюдаются те же случаи разрушения изгибаемых элементов.

Граница между первым и вторым случаем разрушения установлена по предельным деформациям, исходя из условия плоских сечений.

X/h₀ = ε_b ^u /( ε_b ^u + ε_s ^u); X = h₀[(ε_b ^u /( ε_b ^u + ε_s ^u)];

(ε_b ^u /( ε_b ^u + ε_s ^u) = ξ; X = ξ h₀ ; ξ = x/h₀;

23. Граничная высота сжатой зоны бетона

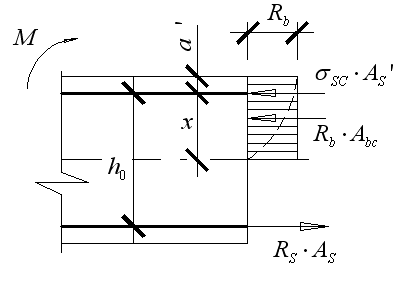
σs c*As’ – усилия в сжатой А;

σs c=Rsc

Rb*Abc –усилия в сжатой зоне Б

Rs*As – усилия в

σs *As растянутой арматуре

Условие прочности для всех сечений записывается как сумма моментов центров тяжести растянутой А

М≤ R_b A_bc (h₀ – 0,5x) + σ_sc ^’ A_s ^’ (h₀ - a^’ ); (1)

Rs*As-Rb*Abc-Rsc*As’=0

σ s*As-Rb*Abc-Rsc*As’=0

На основе большого числа экспериментов было установлено, что σ_s зависит от относительной величине сжатой зоны бетона ξ = x/h₀.

Использование высоты сжатой зоны Б в качестве основного параметра для определения σ_s имеет ряд преимуществ, поскольку “x” качественно отражает особенности напряжённого состояния сечения, а именно учитывает совокупность влияния многих параметров (вид и количество арматуры, прочность и деформативность Б). Поэтому зависимость σ_s – ξ принимает универсальный характер как для изгибаемых, так и для внецентренно сжатых элементов.

Обработка результатов экспериментов показала, что в предельном состоянии зависимость между ε_s – ξ носит гиперболический характер.

Н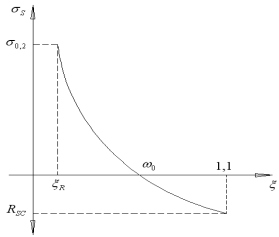 а графике имеются три характерные точки : ξ = ξ_R при σ_s = σ_0,2 напряжения в А=условному или физ.пределу текучести.

ξ = 1,1 при σ_s = R_sc напряжения в А=сжимающим напряжениям

и ξ = ώ₀ при σ_s = 0 или σ_s = σ_sp напряжения в А=0

Граничная высота сжатой зоны бетона ξ_R это такая величина, при которой предельное состояние элемента наступает одновременно с достижением в растянутой арматуре напряжения, равного расчётному сопротивлению R_s , а напряжения в Б=призменной прочности Rb

Для элементов без предварительного напряжения граничная высота сжатой зоны бетона определяется по формуле:

ξ_R = 0,8/(1 + R_s /700).

Для элементов с предварительным напряжением граничная высота сжатой зоны бетона определяется по формуле пособия