1.История развития науки «ЖБ». Нов стр-ный мат-ал – ЖБ, получивший всеобщее признание, оказывает сильное влияние на развитие совр арх-ры. Сейчас можно с полной уверенностью сказать, что для жбк найдены свои, присущие только этому материалу формы. Появилась новая эстетика – эстетика жб. Над проблемами эстетики жб задумывались не только арх-ры, но и инж, создававшие из этого мат-ла выдающиеся конст-ции.
Появление жб означало подлинный переворот в стр-ной технике и, как всякий переворот, поставило трудные проблемы, которые мы до сих пор не сумели разрешить полностью. Одна из них – проблема сотрудничества между арх-ром и стр-лем.
Многие выдающиеся современные сооружения из жб являются результатом деят-ти 1го человека, обладающего знаниями и арх-ра, и инж-ра, и стр-ля. Таковые - Нерви, Кандела, Торроха.
Констр-ия настолько важная часть здания из жб, что чаще всего правильное решение её является залогом совершенства, красоты и эконом-ти соор-ния.
Внедрение новых кон-ций порождает новые арх стили. Египет - столбы и перемычки, Греция - ферма, римляне развили бетонные своды.
ЖБ- продукт развития строительства 19 века. Развитие ЖБ связано с 3мя событиями: 1) создание иск вяжущих; 2) применение стали и чугуна; 3) повторное открытие Б.
Римляне широко применяли Б, однако он полностью исчез в 16, 17, 18 веках
Впервые повторно Б был применён в 18 веке при стр-ве плотины на реке Колдер по проекту Смитона.
В Англии в начале 19 века открытие приобретает широкое значение. Б, основанный на гидравлической извести, заменяет деревянные сваи в основаниях. Например, при стр-ве Вестминстера. Во Франции Б применяется при сооружении фундаментов.
В России рус мастера применили АРМ-ный Б ещё в 1802 году при стр-ве Царскосельского дворца. Однако они не считали, что они открыли совершенно новый материал.
Джон Смитон был 1ым, кто вступил на правильный путь изготовления цемента. В 1824 году появился портландцемент – инж Аспдин.
3им наиболее важным событием, обусловившим открытие ЖБ, было внедрение в стр-во чугуна.
В 1829 году англ инж Фокс сконструировал Б перекрытия, в которых Б применялся в виде заполнения между Ме балками
Следующая стадия в развитии ЖБ наступила тогда, когда строители осознали, что между Б и Ме сущ сцепление, и если в конструкции возникает изг моменты, то растягивающее усилие воспринимается Ме, сжимающее – Б. Не зависимые друг от друга изобретения таких инж, как Вилькинсон в Англии, Монье во Франции, Уард в США, привели к рождению ЖБ.
В 1867 Монье получил патент на А цемент.
В 1877 амер ученый Хайэтт опубликовал книгу, в которой он привел данные по испытанию ЖБ балок. Он применял полосовую и круглую сталь в растянутых зонах балок, впервые доказал, что разрушение балок зависит от кол-ва А. Он предложил плиту-панель, кот состояла из отдельных балок, монолитное перекрытие без балок. Иссл-ем св-тв ЖБ занимался нем инж Кённен, кот создал фирму Монье- строит компания по Б и ЖБ. Его иссл-ния создали основу для простых расчётов прочности плит, перекрытий, сводов и т.д.
В 1892 году он предложил новую систему ЖБ перекрытия. Большую роль в исслед ЖБ сыграл фр инж Генебик: предложил систему жб перекрытий, состоящую из mb и sb. Он предложил констр для жил зданий пролётом 10 м, консоли длиной 3 метра, спиральные лестницы со свободным опиранием.
В 1891 году в Петербурге Н.А. Белялюбский открыл лабораторию, где проводил эксперименты и исследования над жб конструкциями. К концу XIX века сложилась в общих чертах теория жб по допускаемым напряжениям, основанная на методах сопротивления упругих материалов.
Распр жб в дореволюционной России в значит мере способствовали рус инж: А.Ф. Лолейт, И.С. Подольский, Г.П. Передерий и др. После революции началось восстановление разрушенного хозяйства. В конце 20-х годов создаются проектные организации, в задачу которых входит разработка проектов крупных промышленных предприятий, НИИ по изучению ЖБ: ЦНИПС, НИИЖБ, ЦНИИС. В стр-ую практику с 1928 года входят новые тонкостенные пространственные конструкции, разработанные А.А. Гвоздевым, П.Л. Пастернаком, В.З. Власовым и др.
В конце 1931 года А.Ф. Лолейт выступил с предложением по новой теории жб– расчёт по разрушающим нагрузкам. Гвоздев в 1955 предложил теорию расчета жбк по предельным состояниям
Эту теорию развивали А.П. Васильев, С.А. Дмитриев.
В настоящее время происходит актуализация нормативных документов по расчетам жбк. В 2009 вышел закон ФЗ – 384о тех регламенте в стр-ве .
2.Определение понятия бетон, продольные деформации бетона при кратковременном приложении нагрузки. Физико-механические свойства бетона
Б по своему составу представляет композитный, синтетический материал и включает: инертные – щебень, гравий, песок; вяжущие – цементы; воду; добавки. При затворении водой смеси инертных и цемента начинается взаимодействие цем и воды, результатом чего является образование цементного теста – пластической структуры из частиц цемента в воде. При перемешивании Б смеси, цем тесто обволакивает зёрна заполнителя и, постепенно затвердевая, обращает всю массу в монолитное твёрдое тело.
По структуре: плотные; крупнопористые; поризованные; ячеистые. По виду вяжущих: цементые; силикатные; шлаковые. По виду заполнителя: пористый заполнитель, плотный. По виду твердения: естественного твердения, подверженные тепловой обработки при атм давлении, или автоклавная обработка.
Деформации бетона под действием внешних нагрузок
Деформации, возникающие под действием нагрузок, подразделяются на деф от кратковременных нагрузок и длительных нагружений. Они развиваются в продольном и поперечном направлениях.
Продольные деф-ции. Кратковр-ное приложение нагрузки
П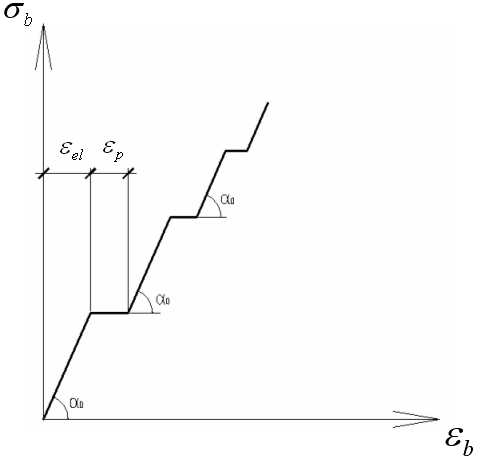
ри
однократном приложении нагрузки в Б
возникают первичные деформации. При
ступенчатом приложении нагрузки и с
выдержкой после каждой ступени диаграмма
σ–ε будет иметь ступенчатое очертание.
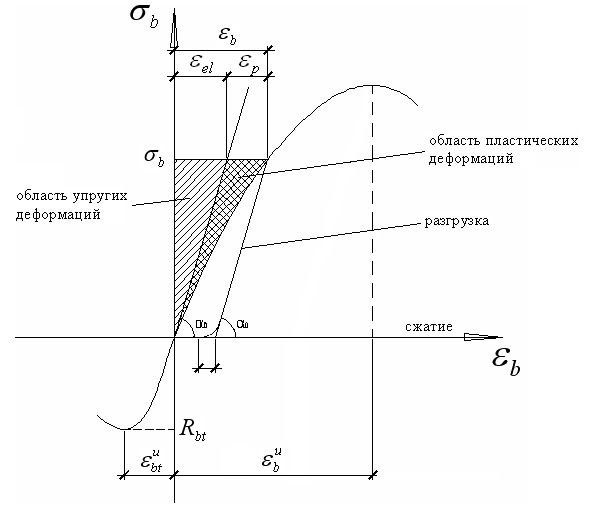
Деф, измеренные в момент приложения нагрузки, носят упругий характер (εel) и связаны с напряжением линейной зависимостью. Деформации, появляющиеся за время выдержки нагрузки, носят неупругий характер и называются пластическими. Величина их зависит от скорости приложения нагрузки . С ↑ кол-ва ступеней и уменьшения нагрузки на каждую ступень неупругие деформации проявляются более явно и диаграмма σ–ε становится криволинейной .
При снятии нагрузки при напряжениях σb упругие напряжения восстанавливаются, восстанавливается и часть неупругих деформаций. С течением некоторого времени восстанавливается ещё около 10% неупругих деформаций, так называемые деформации упругого последействия (εel,p).
Деформации бетона εb состоят их двух частей: εel – упругой части и εp – неупругой, т.е. εb= εel+ εp
3.Продольные деформации бетона при длительном приложении нагрузки.
При действии длительной нагрузки неупругие деформации продолжают развиваться, даже если нагрузка больше не увеличивается (рис.3).
рис.3
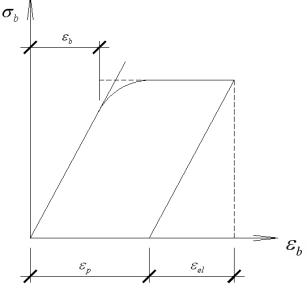Рис.
4
Отрезок 0 – 1 характеризует деформации при нагружении образца, а 1 – 2 при постоянной величине напряжений. Свойство Б претерпевать неупругие деформации при постоянных напряжениях называется ползучестью Б.
Экспериментами установлено, что при напряжениях 0.3 – 0.6 кубиковой прочности Б, зависимость между деформациями ползучести и напряжениями можно условно принять линейной. При большей величине длительных напряжений появляется нелинейная ползучесть. В момент перед разрушением появляются пвсевдопластические деформации. Такая связь весьма условна, т.к. связь между деформациями и напряжениями в бетон всегда нелинейная и границы установить трудно.
4.Поперечные деформации бетона, предельные деформации бетона. Поперечные деформации бетона
Под действием нагрузки возникают также поперечные деформации, которые характеризуются коэффициентом Пуассона νb,p – это отношение относительной поперечной деформации к относительной продольной. Коэффициент Пуассона в области линейной ползучести равен 0.13 – 0.22. В качестве характеристики отношения продольных и поперечных деформаций принят ещё коэффициент ν, это отношение приращения поперечной деформации к приращению продольной. Начало возрастания ν характеризует начало разрыхления бетона. При ν = 0.5 наступает предел деформаций бетона без нарушения его сплошности. С дальнейшим увеличением ν начинаются микроразрушения с развитием микротрещин.
Предельные деформации бетона
Предельными называют такие деформации бетона, при которых начинается разрушение бетона. Различают предельную растяжимость и предельную сжимаемость бетона.
Экспериментами установлено, что предельная сжимаемость при непродолжительном действии нагрузки принято εb0 =0,002.
Предельная растяжимость при непродолжительном действии нагрузки εbt0 = 0,0001. Предельная растяжимость и предельная сжимаемость увеличивается при длительном приложении нагрузки и с повышением прочности и плотности и определяется по таблице 5.6 (СП 52-101-2003 Бетонные и железобетонные конструкции без предварительного напряжения. Свод правил). Предельная растяжимость εbt0 имеет большое значение для обеспечения трещиностойкости железобетонных конструкций.
Коэффициент ползучести φb,cr принимается по таблице 5.5 (СП 52-101-2003).
5.Начальный модуль упругости бетона. Модуль деформации бетона
Для упругого материала зависимость между σ–ε линейная. Бетон упругопластический материал и зависимость между σ–ε нелинейная. Поэтому использование только модуля упругости, характеризующего только упругие свойства материала недостаточно. В расчётах используют начальный модуль упругости, модуль полных деформаций, средний модуль упругопластического бетона, динамический модуль упругости бетона. Рассмотрим зависимость между деформациями и напряжениями.
Начальный модуль упругости бетона
Начальный модуль упругости бетона соответствует мгновенному загружению образца до небольших напряжений и измеряется тангенсом угла наклона касательной к кривой в точке начала координат
(рис. 5).
Рис. 5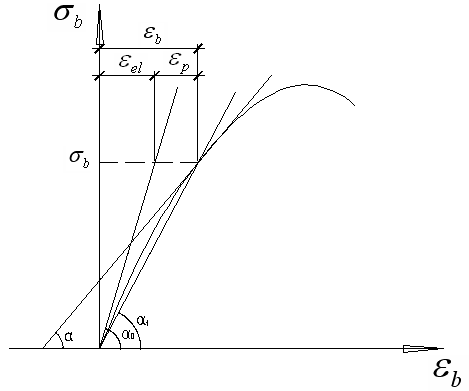
Еb =tg α0 ; σb = Еb* εel ; Еb = σb/ εel ;