3.5 Транспортная сеть с максимальным потоком в сети.

Выберем часть сети из нашей сети предприятия которая будет являться транспортной и найдём максимальный поток.

I). Насыщение потока

1.Пронумеруем вершины сети

2.Насыщаем пути из 0 в 9:

1 ) 0 2 1 2 4 2 7 2 9 условно разрываем насыщенное ребро

1 2 4 (показано штриховкой на рисунке 5)

2 ) 0 4 1 2 3 2 6 2 9 условно разрываем насыщенное ребро

0 4 1

3 ) 0 2 2 2 5 2 8 2 9 условно разрываем ребро 2 2 5

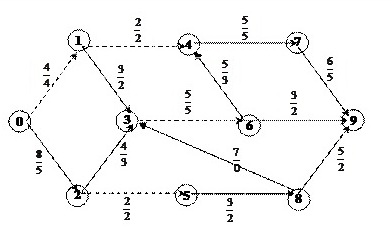
Рисунок 11 - Часть транспортной сети

4) 0 3 2 3 3 3 6 3 4 3 7 3 8 условно разрываем

н асыщенное ребро 3 3 6

Сеть насыщенна и "разорвана". Поток текущий по сети: 5+2+2=9

Рисунок 12 - Насыщенная и "разорванная" сеть

II) Ищем максимальный поток в сети.

Пометим все возможные вершины сети.

1) Вершину 0 пометим -0

2) Непомеченные вершины, смежные с вершиной 0, - это вершины 1 и 2.

В ершину 1 из вершины 0 пометить нельзя, так как ребро 0 4 1 насыщенно.

П ометим вершину 2 меткой +0, поскольку ребро 0 3 2 не насыщенно.

3 )Непомеченные вершины, смежные с вершиной 2, - это вершины 3 и 5. Вершину 5 из вершины 2 пометить нельзя, так как ребро 2 2 5 насыщенно.

П ометим вершину 3 меткой +2 поскольку ребро 2 3 3 не насыщенно.

4 )Непомеченные вершины, смежные с вершиной 3, - это вершины 1,6 и 8. Вершины 5 и 8 из вершины 3 пометить нельзя, так как ребро 3 3 6 насыщенно, а ребро 3 3 8 - пустое. Пометим вершину 1 меткой -3, поскольку ребро 1 2 3 не насыщенно.

Вывод: Никакие другие вершины пометить нельзя. Вершина 9 осталась непомеченной. Следовательно, найденный поток, равный девяти, является максимальным.

4 Линейное программирование

Линейное программирование — математическая дисциплина, посвящённая теории и методам решения экстремальных задач на множествах  -мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.

Линейное программирование является частным случаем выпуклого программирования, которое в свою очередь является частным случаем математического программирования. Одновременно оно — основа нескольких методов решения задач целочисленного и нелинейного программирования. Одним из обобщений линейного программирования является дробно-линейное программирование.

Многие свойства задач линейного программирования можно интерпретировать также как свойства многогранников и таким образом геометрически формулировать и доказывать их.

Математические исследования отдельных экономических проблем, математическая формализация числового материала проводилась ещё в XIX веке. Приматематическом анализе процесса расширенного производства использовались алгебраические соотношения, анализ их проводился с помощью дифференциального исчисления. Это давало возможность получить общее представление о проблеме.

Развитие экономики потребовало количественных показателей, и в 1920 годы был создан межотраслевой баланс (МОБ). Он то и послужил толчком в деле создания и исследования математических моделей. Разработка МОБ в 1924—1925 годах в СССР повлияла на работы экономиста и статистика Василия Васильевича Леонтьева. Он разработал межотраслевую модель производства и распределения продукции.

В 1938 году Леонид Витальевич Канторович в порядке научной консультации приступил к изучению чисто практической задачи по составлению наилучшего плана загрузки лущильных станков (фанерный трест). Эта задача не поддавалась обычным методам. Стало ясно, что задача не случайная.

В 1939 году Леонид Витальевич Канторович опубликовал работу «Математические методы организации и планирования производства», в которой сформулировал новый класс экстремальных задач с ограничениями и разработал эффективный метод их решения, таким образом были заложены основы линейного программирования.

Изучение подобных задач привело к созданию новой научной дисциплины линейного программирования и открыло новый этап в развитии экономико-математических методов.

В 1949 году американский математик Джордж Бернард Данциг разработал эффективный метод решения задач линейного программирования (ЗЛП) — симплекс-метод.

Термин «программирование» нужно понимать в смысле «планирования» Он был предложен в середине 1940-х годов Джорджем Данцигом, одним из основателей линейного программирования, ещё до того, как компьютеры были использованы для решения линейных задач оптимизации.

Метод внутренних точек был впервые упомянут И. И. Дикиным в 1967 году.

Общей (стандартной) задачей линейного программирования называется задача нахождения минимума линейной целевой функции (линейной формы) вида: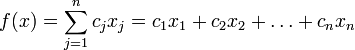

задача в которой фигурируют ограничения в форме неравенств, называется — основной задачей линейного программирования (ОЗЛП)

,

.

Задача линейного программирования будет иметь канонический вид, если в общей задаче вместо первой системы неравенств имеет место система уравнений с ограничениями в форме равенства:

,

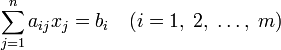Основную задачу можно свести к канонической путём введения дополнительных переменных.

Задачи линейного программирования наиболее общего вида (задачи со смешанными ограничениями: равенствами и неравенствами, наличием переменных, свободных от ограничений) могут быть приведены к эквивалентным (имеющим то же множество решений) заменами переменных и заменой равенств на пару неравенств.

Легко заметить, что задачу нахождения максимума можно заменить задачей нахождения минимума, взяв коэффициенты   с обратным знаком.