2 Решение задачи.

Дано: Решение

λ=780нм=7,8·10-7м h=2мм=2·10-3м R=155см=1,55м n=9

rn-?

Рисунок:

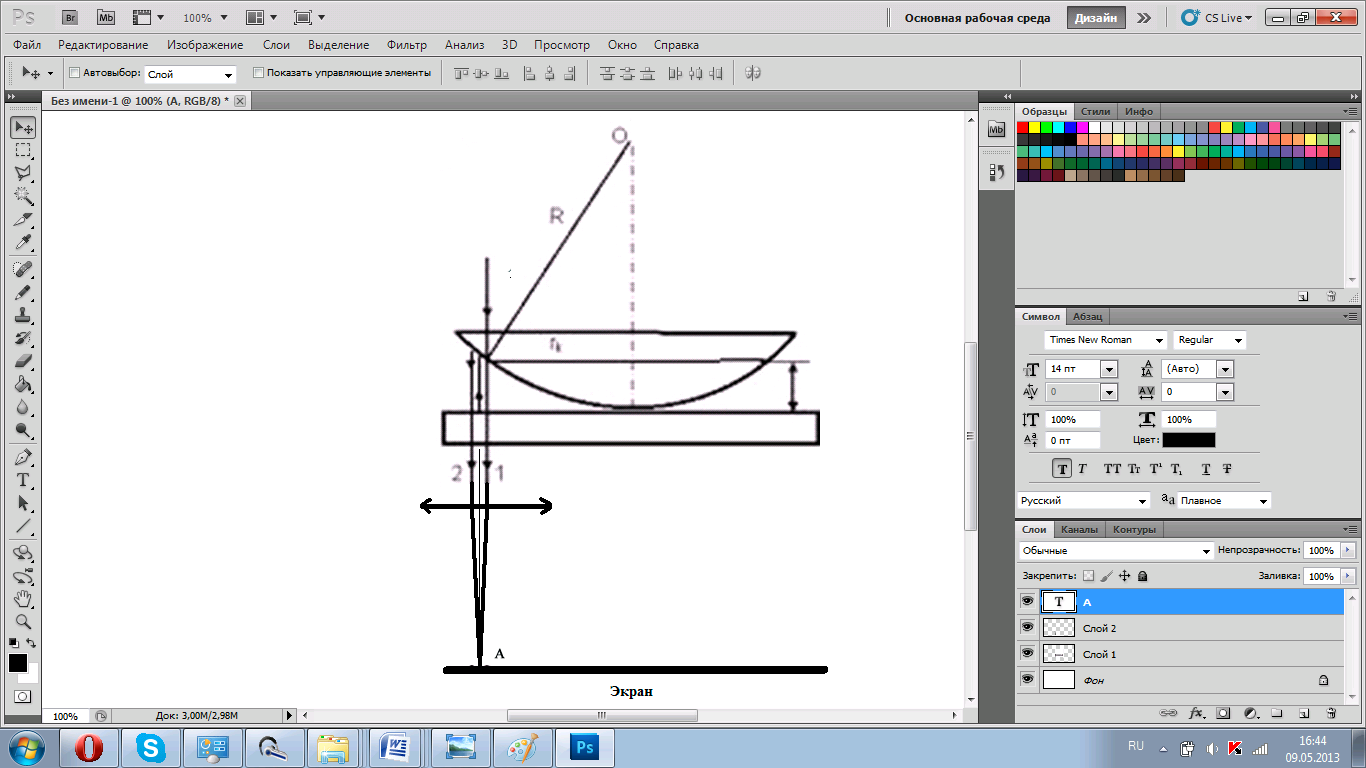
На рисунке представлена картина для линзы без сошлифованной площадки. Интерференция наблюдается в точке А на экране. Точка А , расположена в фокусе собирающей линзы, а экран – в фокальной плоскости.

Чтобы использовать формулы, выведенные для такой конструкции, нам необходимо найти номер – m минимума (темного кольца), с которого начинает совпадать интерференционная картина для нашей конструкции и той, что представлена на рисунке.

Для этого приравняем правые части уравнений для радиуса сошлифованной части (2) и радиуса k-го темного кольца (3). Полученное значение k округлим в большую сторону и тем самым получим искомое значение m.

Как уже говорилось выше, при двукратном отражении второго луча на границе раздела воздух-стекло, происходит изменение фазы на 2π. То есть, к оптической длине пути для второго луча следует добавить одну длину волны, но делать этого не будем из соображений простоты вычислений, так как это не внесет никаких изменений в полученные результаты и лишь добавит единицу к номеру каждого кольца, то есть нумерация началась бы с двойки, а не с единицы. Нам этого не нужно, поэтому равенство примет следующий вид:

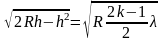
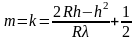при округлении до целого в большую сторону.

Теперь, чтобы найти радиус n-го темного кольца нам необходимо подставить в формулу (3) вместо k значение m+n.

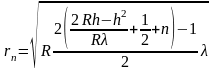
Проверим размерность итогового выражения:

Вычислим искомое значение:

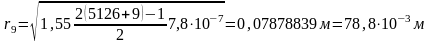
3 Графическая часть работы.

Согласно полученному заданию нам необходимо построить графики зависимостей радиуса темного кольца от высоты сошлифованной части, а также от радиуса сошлифованной части (радиус основания).

1. Зависимость мы, по сути, нашли выше. В данном случае от высоты сошлифованной части зависит лишь то, с какого темного кольца начнут совпадать интерференционные картины для установки без сошлифованной площадки и для установки, где таковая имеется:

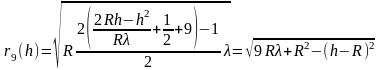
Значения n, R и λ подставим из условия, тогда график зависимости примет вид (рисунок 2):

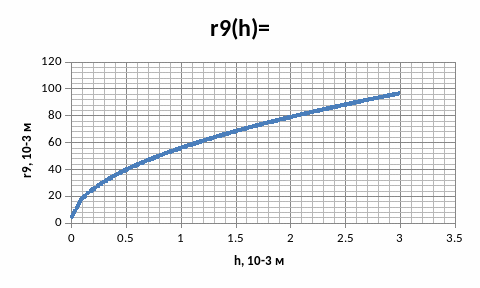
Рисунок 2. Зависимость r₉(h).

Если опустить 9Rλ, как сравнительно малую величину, то:

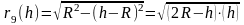
_{В этой формуле в разности 2R-h пренебрежимо малой величиной является уже h, отбросив ее, получаем:}

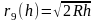
2. Зависимость .

Возведем обе части уравнения (2) в квадрат, получим:

.

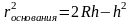Исходя из полученного результата заменим 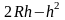на в уравнении, описывающем зависимость r_n(h) и подставим вместо n число 9:

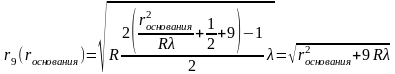
Значения n,R и λ подставим из условия, тогда график зависимости примет вид (рисунок 3):

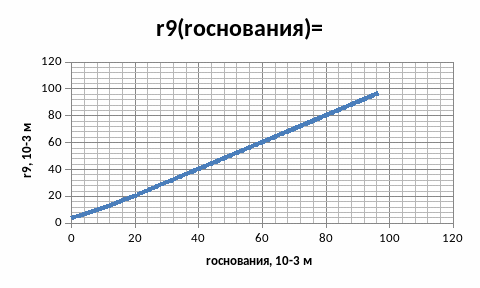
Рисунок 3. Зависимость r₉(r_{основания}).

Выделим формулу для линейной части графика как асимптотическое приближение:

_{При стремлении rоснования к радиусу кривизны поверхности линзы произведение 9Rλ становится пренебрежимо малой величиной, опустив ее, получаем.}

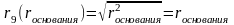
5 Выводы по результатам работы.

По итогам проделанной работы можно сделать вывод о том, что радиус девятого темного кольца напрямую зависит от высоты сошлифованной части линзы и радиуса получившейся в результате площадки.

Эту зависимость я представил графически на рисунках 1 и 2 соответственно.

По виду графиков этих зависимостей можно судить о характере зависимости. Так зависимость радиуса девятого темного кольца от высоты сошлифованной части имеет характер 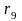~ . Что касается зависимости радиуса девятого темного кольца от радиуса сошлифованной площадки, то она имеет такой вид: ~ .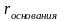