3. Найти максимальное значение функции f(X) с учётом системы ограничений задачи, используя:

а) условия теоремы Куна-Таккера.

Составляем функцию Лагранжа:

L(x,λ)= F(x)+λ^Tg(x)=F(x)+∑λ_j∙g_j(x).

Здесь g_j(x) – левые части ограничений, приведённых к нулевой правой части;

λ_j - неопределённые множители Лагранжа:

g₁(x)=-5x₁+3x₂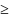 0;

g₂(x)=-x₂+5 ;

Точка экстремума является седловой точкой с максимумом по x и минимумом по λ, поэтому ограничения приведены к виду g_j (x) 0:

L(x,λ)= = -4x₁²-5x₂²+5x₁x₂+x₁+3x₂ +λ₁(-5x₁+3x₂)+λ₂(-x₂+5) .

Условия теоремы Куна – Таккера записываем следующим образом:

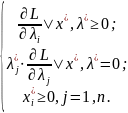
Частные производные функции Лагранжа определяются выражениями:

=-8x₁+5x₂+1-5λ₁ ;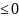

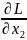=5x₁-10x₂+3+3λ₁-λ₂ ;

=-5x₁+3x₂ ;

=-x₂+5 ;

Для приведения неравенств к виду равенств вводятся дополнительные неотрицательные переменные v и w. Одновременно свободные члены переносятся в правую часть, тогда:

-8x₁+5x₂-5λ₁+v₁=-1;

5x₁-10x₂+3λ₁-λ₂+v₂=-3;

-5x₁+3x₂-w₁=0;

-x₂-w₂=-5.

Решение этой системы из четырёх алгебраических уравнений, содержащих восемь неизвестных, можно найти с помощью симплекс – процедуры. На первом шаге в базис включаются все введённые дополнительные

переменные. Строка для функции цели отсутствует. Процедура решения иллюстрируется симплекс – таблицами.

Б П	СЧ	НП
		x1	x2
v1	-1	-8	5	-5	0
v 2	-3	5	-10	3	-1
w1	0	5	-3	0	0
w2	5	0	1	0	0

БП	СЧ	НП
		x1	v2
v 1	-25/10	-55/10	1/2	-35/10	-1/2
x2	3/10	-1/2	-1/10	-3/10	1/10
w1	9/10	35/10	-3/10	-9/10	3/10
w2	47/10	1/2	1/10	1/2	-1/10

БП	СЧ	НП
		v1	v2
x1	5/11	-2/11	-1/11	7/11	1/11
x2	29/55	-1/11	-8/55	1/55	8/55
w 1	-38/55	7/11	1/55	-172/55	-1/55
w2	246/55	1/11	8/55	-1/55	-8/55

БП	СЧ	НП
		v1	v2	w1
x1	594/1892	-99/1982	-165/1892	35/172	165/1892
x2	495/946	-165/1892	-8/55	1/172	8/55
	38/172	-35/172	-1/172	-55/172	1/172
w2	4235/946	165/1892	8/55	-1/172	-8/55

Решение соответствует допустимому базисному решению: x₁=0,31; x₂=0,52; =0,22; w₂=4,48; v₁, x₂, , =0.

Кроме того, выполняется условие:

x₁ v₁= x₂v₂=0;

λ₁ w₁=λ₂w₂=0.

Поэтому x₁^*=0,31; x₂^*=0,52 является оптимальным решением задачи: F_max=0,946.

б) метод допустимых направлений Зойтендейка.

Находим направление вектора градиента в точке x⁰:

F(x⁰)=[8;-22].

Тогда координаты очередной точки (смотреть метод наискорейшего спуска):

;

Определяем интервал допустимых значений для параметра , при котором точка x¹ будет принадлежать ОДЗП. Для этого координаты точки x¹ подставляются в ограничения задачи:

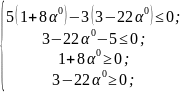
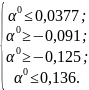
Выбираем наиболее сильные из полученных условий:

.

Находим величину , которая обеспечит максимум функции F(x). Процедура полностью совпадает с первым шагом решения задачи методом наискорейшего спуска, поэтому 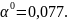Но это точка не попадает на интервал. Берём

=1+8 =1+8∙0,0377=1,302;

=3-22 =3-22∙0,0377=2,171.

Вычисляем составляющие вектора градиента в точке x¹:

F(x¹) = [1,44; -12,2].

Движение в направлении 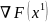выходит за пределы ОДЗП, поэтому очередная точка поиска вычисляется по выражению: , где 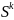– новое направление, которое составляет минимальный острый угол с вектором градиента и направлено по границе ОДЗП. При этом следующая точка должна принадлежать ОДЗП, а функция цели увеличивается максимальным образом.

Направление находим как решение задачи:

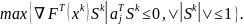
Направление 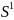очередного шага определяем из условия:

,

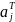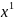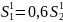где - вектор коэффициентов при переменных в первом ограничении, на котором находится точка . Отсюда следует, что . Тогда из 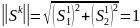находим .

.

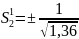
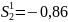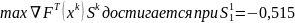Координаты точки x² определяются как:

.

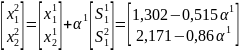Находим интервал изменения , при котором x² принадлежит ОДЗП (первое ограничение опускаем):

Выбираем наиболее сильные из полученных условий:

Первое ограничение опущено, т.к. точка x¹ принадлежит соответствующей прямой.

Находим , которое обеспечит максимум функции в направлении .

.

.

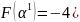
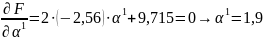Значение принадлежит найденному интервалу.

Вычисляем координаты точки x²:

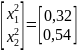
Вычисляем составляющие вектора градиента в точке x²:

F(x²) = [1,14; 0,8].

Направление вектора F(x²) перпендикулярно направлению s¹, следовательно, найденная точка x²[0,32; 0,54] обеспечивает максимум функции F(x) с учётом ограничений на переменные: F_max = 0,93.

Графическая интерпретация к методу допустимых направлений Зойтендейка дана в приложении №1, рисунок 3.

в) метод линейных комбинаций.

Суть метода линейных комбинаций заключается в линеаризации функции F(x) и замене её линейной функцией w(x) в соответствии с выражением:

w(x)= F(x)^T∙x

Находим направление вектора градиента в точке x⁰; F(x⁰)=[8;-22], в соответствии с этим:

w(x⁰)=[8; -22]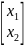 = 8x₁ - 22x₂ ;

Решаем задачу линейного программирования w(x⁰)= 8x₁-22x₂ (max) при ограничениях:

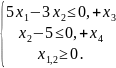
БП	Свободные члены	x1	x2
x 3	0	5	-3
x4	5	0	1
w	0	-8	22

БП	Свободные члены	x3	x2
x1	0	1/5	-3/5
x4	5	0	1
w	0	8/5	86/5

В результате получаем одну из вершин ОДЗП x^0*=[0;0]. Это оптимальное решение линеаризованной задачи.

Произведём корректировку найденного решения в соответствии с выражением:

x¹=x⁰+ (x^0*- x⁰);

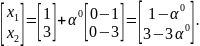
Находим значение 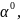которое максимизирует F(x¹):

F( ) = ;

;

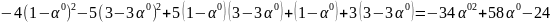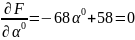=0,853.

= 1 - = 0,147;

= 3 - 3 = 0,441.

Осуществляем линеаризацию относительно найденной точки x¹.

F(x¹)=[2,029; 0,53].

Решаем задачу линейного программирования w(x¹)= 2,029x₁+0,53x₂ (max) при ограничениях:

БП	Свободные члены	x 1	x2
x 3	0	5	-3
x4	5	0	1
w	0	-2,029	-0,53

БП	Свободные члены	x3	x2
x1	0	1/5	-3/5
x 4	5	0	1
w	0	2/5	-1,74

БП	Свободные члены	x3	x4
x1	3	1/5	3/5
x2	5	0	1
w	0	2/5	1,74

В результате получаем одну из вершин ОДЗП x^1*=[3; 5]. Это оптимальное решение линеаризованной задачи.

Произведём корректировку найденного решения в соответствии с выражением:

x²=x¹+ (x^1*- x¹);

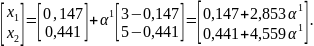
Находим значение 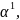которое максимизирует F(x²):

F( ) = ;

;

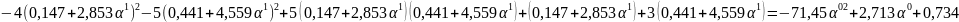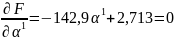=0,019.

= =0,3;

= =0,53.

В результате получаем:

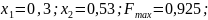
Графическая интерпретация к методу линейных комбинаций дана в приложении №1, рисунок 4.