Задание №3 Нелинейное программирование
Целевая функция задана выражением:
F(x) = -4x12-5x22+5x1x2+x1+3x2
Линейные ограничения неравенств имеют вид:
1. Построить область допустимых значений переменных. Внутри области выбрать точку x0,которая в дальнейшем будет являться начальной в процессе поиска экстремума.
Область допустимых значений переменных построена в приложении №1, рисунок 1. Внутри области мы выбираем точку x0=[1;3], которая в дальнейшем будет являться начальной в процессе поиска экстремума.
2. Найти максимальное значение функции F(x) без учёта ограничений задачи, используя:
а) метод Ньютона – Рафсона.
Во-первых, посмотрим вид функции цели в пакете Matlab, используя подпрограмму:
>>[x1,x2]=meshgrid([-4:0.1:4]);
>>F=-4*x1.^2-5*x2.^2+5*x1*x2+x1+3*x2;
>>meshc(x1, x2, F)
На рисунке 12 приведён вид функции F(x) = -4x12-5x22+5x1x2+x1+3x2
вместе с проекциями линий уровня: функция выпуклая вверх и имеет максимум.
Рис.12. Вид функции
F(x) = -4x12-5x22+5x1x2+x1+3x2 (max) - заданная функция,
x0=(1;3) – начальная точка.
Очередная точка, по методу Ньютона – Рафсона, вычисляется в соответствии с выражением:
x k+1= x k –H-1(x k)F(x k),
где H(x) – матрица Гессе функции F(x);
H-1(x) – обратная, по отношению к H(x), матрица.
Найдём градиент функции:
;
Найдем градиент функции в точке x 0: F(x 0)=[8; -22].
Запишем матрицу Гессе:
;
,
где detH(x) – определитель матрицы H;
AdjH(x) – присоединённая к H матрица (транспонированная матрица алгебраических дополнений).
Найдём алгебраические дополнения матрицы Н:
11=-10 12=-5
21=-5 22=-8
,
detH=(-8)∙(-10)-5∙5=80-25=55.
Отсюда
;
Найдем очередную точку x 1:
;
Найдем градиент в точке x1:
F (x1)=[0;0].
Следовательно, в точке x1 функция F(х) достигает максимального значения:
Fmax=
1,018.
б) метод наискорейшего спуска.
В методе наискорейшего спуска (подъёма) очередная точка при поиске максимума функции вычисляется по формуле:
xk+1= xk +αkF(x k),
где направление движения задаётся вектором градиента F(x) функции F(x), вычисленном в точке xk , а величина шага определяется числовым параметром αk.
;
Найдем градиент функции в точке x0: F(x0)=[8; -22].
На первом шаге движение осуществляется из точки x0 вдоль вектора F(x0) в новую точку x1:
;
Величина
шага
на любом шаге выбирается из условия
обеспечения экстремума функции в
рассматриваемом направлении. Подставляя
координаты точки x1
в функцию F(x),
получим:
F(
)=-4(1+8
)2-5(3-22
)2+5(1+8
)(3-22
)+(1+8
)+3(3-22
)
= -3556
2+548
-24;
;
В результате первого шага координаты очередной точки получаются равными:
=1+8
=1+8∙0,077=1,616;
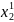=3-22
=3-22∙0,077=1,306.
F(x1)=[-5,398; -1,98].
На
втором шаге движение осуществляется в
направлении вектора F(x1)
с величиной шага
:
;
F(
)=-4(
)2-5(
)2
+
5(
)(
)+(
)+3(
)=
-82,712
2+33,056
;
;
=
=
∙
0,2 = 0,536;
=
=
= 0,91.
F(x2)=[1,262; -3,42].
На
третьем шаге движение осуществляется
в направлении вектора F(x2)
с величиной шага
:
;
F(
)=-4(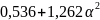
)2-5(0,91
+
5(
(0,91
)+(
)+
3(
-86,432
2+13,285
+0,418;
;
=
=
=
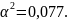
0,633;
=
=
=
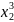0,647.
Экстремум функции после трёх шагов:
Fmax = 0,926.
Графическая интерпретация к методу наискорейшего спуска дана в приложении №1, рисунок 2.
На плоскости x, y (рис.13) приведены линии уровня функции цели F, построенные в Matlab, в соответствии с подпрограммой:
>>[x,y]=meshgrid([-2:0.1:2]);
>>F=-4*x.^2-5*y.^2+5*x.*y+x+3*y;
>>figure;
>>cl=[-10 -8 -6 -4 -2 -1 -0.2 0.5 0.9];
>>[c,h]=contour(x,y,F,cl,'r');
>>clabel(c,h);
Рис.13. Линии уровня
Центр концентрических линий является точкой экстремума x*.