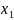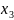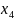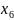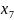Задание №2. Линейное программирование

1. Составить математическую модель задачи. Найти оптимальный план x^* и экстремальное значение функции.

Найти минимальное значение функции F(x)=5x₁+3x₂-3x₄ при следующих ограничениях:

;

;

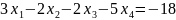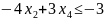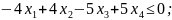
Умножим второе ограничение на (-1) и введём в ограничения дополнительные переменные 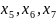и искусственную переменную R следующим образом:

;

;

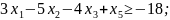
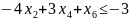Найдем минимум целевой функции симплекс методом. В симплекс таблицу вводится дополнительная строка штрафной функции (M), подлежащая обязательному обнулению.

Пусть 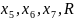– базисные переменные, а x₁ x₂ ,x₃, x₄ – небазисные. Функция цели:

F (x) =F(x)+M∙∑R= В первой симплекс – таблице коэффициенты при небазисных переменных в F – строке и M – строках знака не меняют, так как осуществляется минимизация функции. А свободный член в M – строке берётся с противоположным знаком.

БП	Свободные Члены	Небазисные переменные
R	-18	3	-2	-2	-5
	-18	3	-5	-4	0
	-3	0	-4	0	3
	0	-4	4	-5	5
F	0	5	3	0	-3
M	18	-3	2	2	5

Выбираем ведущий столбец и строку в соответствии с алгоритмом решения. Оптимизация ведётся по М строке. В результате x₄ введём в базис, а переменную R исключим из рассмотрения, сократив количество столбцов.

БП	Свободные Члены	Н ебазисные переменные
	18/5	-3/5	2/5	2/5
	-18	3	-5	-4
	-69/5	9/5	-26/5	-6/5
	-18	-1	2	-7
F	54/5	16/5	21/5	6/5
M	0	0	0	0

Решение не является допустимым, т.к. в столбце свободных членов имеются отрицательные элементы.

Выбираем ведущий столбец и строку в соответствии с алгоритмом решения. В результате введём в базис, а переменную исключим из него.

БП	Свободные Члены	Н ебазисные переменные
	54/25	-9/25	2/25	2/25
	18/5	-3/5	-1/5	4/5
	123/25	-33/25	-26/25	74/25
	-126/5	1/5	2/5	-43/5
F	-108/25	143/25	21/25	-54/25

Решение не является допустимым, т.к. в столбце свободных членов имеется отрицательный элемент.

В ыбираем ведущий столбец и строку в соответствии с алгоритмом решения. В результате введём в базис, а переменную исключим из него.

БП	Свободные Члены	Небазисные переменные
	414/215	-77/215	18/215	2/215
	54/43	-25/43	-7/43	4/43
	-807/215	-269/215	-194/215	74/215
	126/43	-1/43	-2/43	-5/43
F	432/215	1219/215	159/215	-54/215

Решение не является допустимым, т.к. в столбце свободных членов имеется отрицательный элемент.

Выбираем ведущий столбец и строку в соответствии с алгоритмом решения. В результате введём в базис, а переменную исключим из него.

БП	Свободные Члены	Н ебазисные переменные
	3	-77/269	92/269	-24/269
	3	-125/269	69/269	-18/269
	3	-215/269	194/269	-74/269
	3	-5/269	-8/269	-33/269
F	-15	1219/269	-901/269	352/269

Решение является допустимым, но не оптимальным, т.к. в F-строке имеется отрицательный элемент.

Выбираем ведущий столбец и строку в соответствии с алгоритмом решения. В результате введём в базис, а переменную исключим из него.

БП	Свободные Члены	Небазисные переменные
	153/97	9/97	-92/194	8/194
	375/194	-35/194	-69/194	6/194
	807/194	-215/194	269/194	-74/194
	303/97	-10/194	8/194	-26/194
F	-207/194	159/194	901/194	3/97

Получено оптимальное решение. Искомый минимум функции F(x) равен свободному члену F-строки, взятому с обратным знаком, так как min F(x) = -max (-F(x));

F_min= 1,07.

Решение задачи в MatLab:

>>F=[5 3 0 -3];

>> A=[3 -5 -4 0; 0 -4 0 3; -4 4 -5 5; -1 0 0 0; 0 -1 0 0; 0 0 -1 0; 0 0 0 -1];

>> B=[-18; -3; 0; 0; 0; 0; 0];

>> Aeq=[3 -2 -2 -5];

>> Beq=[-18];

>> x=linprog(F,A,B,Aeq,Beq)

x =

0

1.9330

3.1237

1.5773

>> Q=F*x

Q = 1.0670