Министерство образования Республики Беларусь

Учреждение образования

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра систем управления

Пояснительная записка к курсовому проекту по курсу: «Математические основы теории систем»

Вариант №11

Принял: Выполнил:

преподаватель студент гр.022403

кафедры СУ Жук Д.А.

Павлова А.В.

Минск 2013

Задание №1 Модели в пространстве состояний

1. Передаточная функция звена (системы) W(s) – это отношение изображения по Лапласу выходного сигнала y(s) к изображению по Лапласу входного сигнала u(s) при нулевых начальных условиях.

Заданная передаточная функция:

Система уравнений общего вида:

Выражение называется характеристическим полиномом системы.

Характеристический полином (знаменатель передаточной функции) является важнейшей характеристикой модели, определяющей устойчивость переходных процессов, их форму и длительность.

а) Передаточная функция в полиномиальной форме:

tf – полиномиальная форма, в которой передаточная функция задается двумя векторами строками, составленными из коэффициентов многочленов числителя и знаменателя в порядке убывания степеней S.

Результаты в MATLAB:

>>W = tf ([2700 8100 6075], [1 21 140 300])

Transfer function:

2700 ^2+8100s+6075

--------------------------------

s^3 + 21 s^2 + 140 s + 300

б) Передаточная функция в zpk форме:

zpk - форма нулей, полюсов и коэффициента усиления, в которой полиномы записаны через их корни: нули числителя – zi, полюса знаменателя - pj.

Результаты в MATLAB:

>> zpk(W)

Zero/pole/gain:

2700( s+1.5)^2

----------------------

(s+10) (s+6) (s+5)

в) Передаточная функция в ss – форме:

>> ss([-21 -140 -300; 1 0 0; 0 1 0], [1; 0; 0], [2700 8100 6075], [0])

a =

x1 x2 x3

x1 -21 -140 -300

x2 1 0 0

x3 0 1 0

b =

u1

x1 1

x2 0

x3 0

c =

x1 x2 x3

y1 2700 8100 6075

d =

u1

y1 0

2. Запишем столбцовую присоединенную каноническую форму.

А - матрица коэффициентов обратных связей, охватывающих интеграторы.

B - матрица коэффициентов связей входов модели и входов интеграторов.

C - матрица коэффициентов связей выходов интеграторов и выходов модели.

D - матрица коэффициентов связей входов и входов модели напрямую, минуя интеграторы.

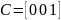, , , D = [0].

Скалярная форма уравнений состояния запишется следующим образом:

Рисунок 1. Структурная схема модели в Simulink

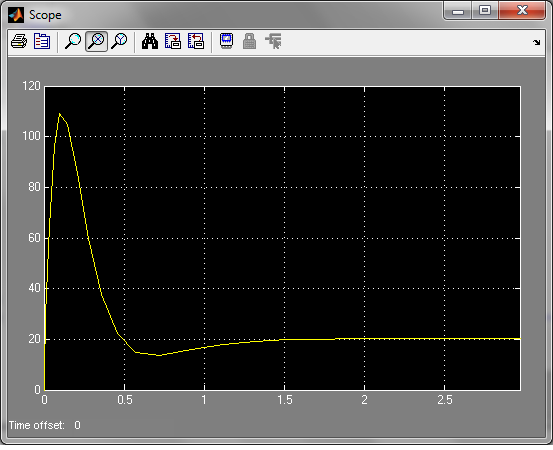
Рисунок 2. Реакция на единичное ступенчатое воздействие.

Переходная характеристика h(t)– это процесс изменения сигнала на выходе системы при подаче на вход единичного ступенчатого воздействия.

>> ss([-21 -140 -300; 1 0 0; 0 1 0], [1; 0; 0], [2700 8100 6075], [0])

>> step(w)

Рисунок 3. Реакция на единичное ступенчатое воздействие

Импульсная переходная характеристика w(t)- процесс изменения сигнала на выходе при подаче на вход δ – функции.

>> impulse(w)

Рисунок 4. Импульсная переходная характеристика

Амплитудно – частотная характеристика показывает, как изменяется отношение выходного сигнала к входному в зависимости от частоты.

Фазочастотная характеристика показывает изменение сдвига фаз между входным и выходным сигналами в зависимости от частоты.

>> bode(w)

Рисунок 5. ЛАЧХ и ЛФЧХ

Амплитудно-фазовая частотная характеристика (АФЧХ) — удобное представление частотного отклика линейной стационарной динамической системы в виде графика в комплексных координатах. На таком графике частота выступает в качестве параметра кривой, фаза и амплитуда системы на заданной частоте представляется углом и длиной радиус-вектора каждой точки характеристики.

>> nyquist(w)

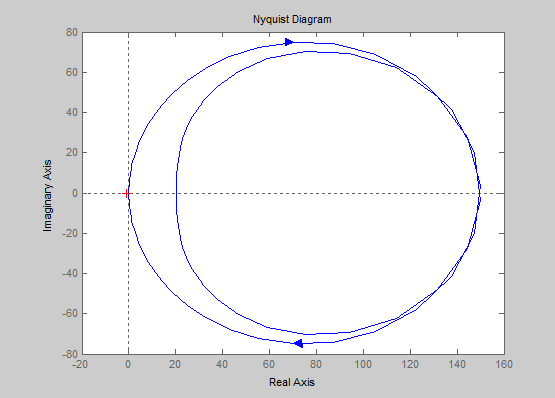
Рисунок 6. АФЧХ