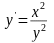Доказать, что
треугольник с вершинами А(-2;-1), В(6;1),
С(3;4) - прямоугольный.
Даны две смежные
вершины параллелограмма А(-2;6), В(2;8) и
точка пересечения его диагоналей
М(2;2). Найти координаты двух других
вершин.
Даны уравнения
двух сторон параллелограмма х – 2у = 0
и х – у – 1 = 0 и точка пересечения его
диагоналей М(3;1). Найти уравнения двух
других сторон.
Найти площадь
треугольника, заключенного между осями
координат и прямой 2х–5у+10 = 0.
Написать уравнение
прямой, проходящей через точки А(2;1),
В(4;1). Найти угловой коэффициент этой
прямой.
Записать уравнение
прямой 2х – у -3 = 0 в отрезках и постройте
ее.
Составить уравнение
прямой, проходящей через начало
координат и точку пересечения прямых:
2х + 5у – 8 = 0 и 2х + 3у +4 = 0
Вычислить: 1)
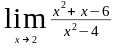 ;
2)
;
2) ;
3)
;
3)
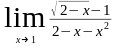
Найти производную
функции:
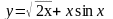
Вычислить
производную
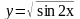 -cos
x3
-cos
x3
Найти производную
функции в точке х = 0, если у = 2lg2x
Найти производную
функции в точке х = 3, если
Вычислить:
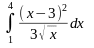
Вычислить:
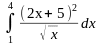
Вычислить:

Найти площадь
фигуры, ограниченной линиями: у = х2–2х+3;
у = 3х– 1.
Найти площадь
фигуры, ограниченной линиями у = 1- х2,
у = х, у = 0
Найти общее решение
уравнения и сделайте проверку
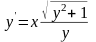
Вычислить:(-1-i)15
Решить уравнение:
х3=
3-3i
Вычислите значение
частной производной функции
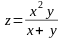 в точке М(-2;3)
в точке М(-2;3)
Решить дифференциальные
уравнения: 1)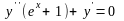 ;
2)
;
2)