19) Характер фундаментальной матрицы ф(t)

1. Система однородных диф.ур. записывается как:

2. Решение системы имеет вид:

3. Сделаем подстановку (2) в (1). Для этого производим диф-ние (2):

В результате получаем:

Выражение (3) сокращаем на . В результате получаем выражение (4):

Ф(t) – это такая матрица, производная которой по времени = произведению матрицы кэфов А на Ф(t).

Аналогичными св-ом обладает ф-я:

При подстановке (6) в ур-е (1) получим:

20)Метод Лагранжа для Решение неоднородной системы дифференциальных уравнений

Неоднородная система линейных дифф. уравнений с постоянным коэффициентом имеет вид:

(1)

- мат-столбец искомых функций

- матрица коэффициент

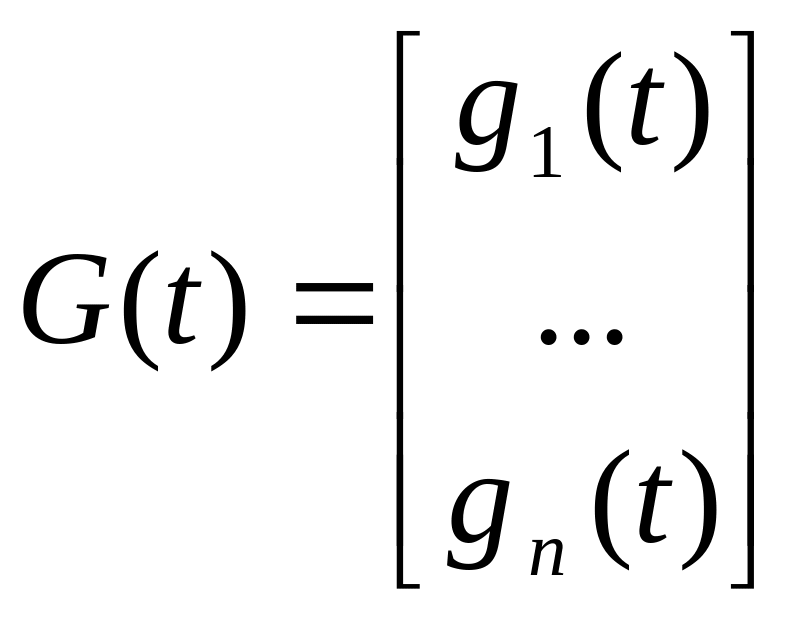- мат столбец правой части системы

Решение неод. сист. состоих из суммы двух решений

- общего решения однородной системы

- частного решения решается за счет правой части

методы нахождения частного решения сист. фид. уравнения

1) Метод Лангажа (трудоемкий) «произв. коэф»

2) Метод «неопред. коэф»

реш. сист 1 имеет вид

(2)

- реш системы

- фундам. матрица решений однород системы

- надо найти

Производим подстан. решения 2 в решение 1

1) расчит. первую производную

(3)

2) Делаем подстановку 3 и 2 в 1

(4)

3) Правую и левую части сокращаем. Делим правую и левую на

: (5)

4) Ищем услов. при t=0 из уравн 2

получаем (6)

5) Интегрируя

(7)

6) Делаем подстановку 6 в решение 2

(8)

В итоге получаем решение неод. сист. дифф. уравнений

(9)

Формула Коши

Это решение рассм. как сумму решений системы однород уравнений и частоного решения неоднород системы

Решение неоднород делится на решение однородной и частной.

22) Элементы вектора G(t) представлены в виде произведения полиномов степени на гармонические ф-ии:

Частное решение в этом случае отыскивается в виде: , (2)

Где , – полином степени (z+s) с неизвестными кэфмаи; z=max( ), (k=1,2,…,n) – максимальная степень полинома .Величина s находится из след. условий:а) s=0, если ( ) не явл. корнем характеристического ур. однородной системы;

б) s=k (k – кратность корня), если ( ) явл. корнем характеристического ур. однородной системы.Неизвестные кэфы полиномов определяются путём подстановки выражения (1) в систему диф ур и приравниванием кэфов при подобных членах ур-й.