3. Лінійні неоднорідні диференціальні рівняння зі сталими коефіцієнтами
Обмежимось випадком рівняннь 2-го порядку.
Загальний вигляд лінійного неоднорідного ДР 2-го порядку зі сталими коефіцієнтами є такий
,
(1)
де
-числа.
Якщо
,
то рівняння
(2)
називається лінійним однорідним ДР 2-го порядку зі сталими коефіцієнтами
Теорема. Загальний розв’язок рівняння (1) визначається формулою
,
Тобто, загальний розв’язок неоднорідного рівняння (1) дорівнює сумі загального розв’язку однорідного рівняння (2) та деякого частинного розв’язку необнорідного рівняння (1)
3.1. Знаходження загального розв’язку лодр (2)
Рівняню (2) ставится у відповідність алгебраічне рівняня
,
(3)
яке називається характеристтичним рівнянням
1-випадок.
корні (3) дійсні та різні
2-випадок.
корні (3) співпадають
3-випадок.
корні (3) комплексні
,
де
Приклад
1. Знайти загальний
розв’язок ЛОДР
.
.
Розв’язуємо характеристтичне рівняння
,
,
,
.
3.2 Розв’язання лінійного неоднорідного др
Обмежимось
важливим для економіки випадком правої
частини вигляду
.
Теорема. Нехай права частина рівняння (1) має вигляд .
1.Якщо
не є корнем характеристтичного многочлена
,
то рівняння (1) має розв’язок
(4)
2.Якщо
є корнем характеристтичного многочлена
кратності
,
то рівняння (1) має розв’язок
(5)
Приклад
2. Знайти загальний
розв’язок лінійних неоднорідних
ДР:
а)
;
б)
;
в)
.
Розв’язання.
а)а)
;
.
.
б) )б)
;
.
.
-
коріль кратності
.
.
.
в)
.
.
співпадає
з двома корнями характеристичного
многочлена., тобто
.
.
.
Задача Коші для лінійного неоднорідного ДР (1) є така
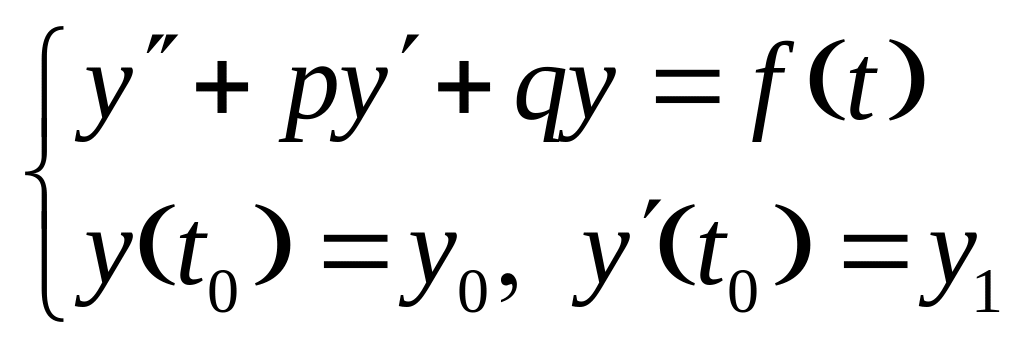
Приклад
3. Розв’язати
задачу Коші: а)
; б)
Розв’язання.
а)
знайдено у прикладі 2,а):
.
,
.
б)
знайдено у прикладі 2,в)
,
.
Модели экономической динамики.
Начнем с простейших моделей макроекономической динамики
1.Естественный рост
Пусть
объем
продукции некоторой отрасли, реализованной
к моменту времени
.
Предполагается, что цена
этой
продукции фиксирована (выполняется
условие ненасыщенности рынка).Тогда
прибыль к моменту времени
составит
Обозначим
величину
инвестиций, направленных на расширение
производства. В модели естественного
роста предполагается, что скорость
выпуска продукции(акселерация)
пропорциональна величине инвестиций.
(1)
Число
называется нормой акселерации или
акселератором. Тут мы пренебрегаем
временем между окончанием производства
продукции и ее реализацией, т.е.
считаем, что инвестиционный лаг равен
нулю.
В более совершенніх моделях принцип акселерации представляется формулой
,
(*)
т.е.
инвестиции пропорциональны приросту
продукции за предшествующий период.
Величина
,
которая характеризует сдвиг во времени
(запаздывание) действия фактора на
результат, в экономике называется лагом.
В выражении (*) лаг
.
Предполагая, что величина инвестиций составляет фиксированную часть прибыли, получим:
,
(2)
Где
коэффициент пропорциональности
(называемый
нормой инвестиций) –постоянная
величина
.
Если подставить выражение для
из
(2) в (1), то приходим к уравнению
,
(3)
где
.
Получено ДР (см. пример 2,с.27 конспекта),
общее решение которого
,
а с учетом начального условия
:
(4)
Замечание 1. Одно и тоже ДР может моделировать разные явления или процессы. Так уравнение (3) описывает также рост народонаселения, динамику роста цен при постоянной инфляции, процесс радиоактивного распада и т.д.
Замечание
2. Логарифмическая производная
называют также относительной скоростью
изменения функции или темпом
изменения функции. Решение уравнения
естественного роста это функция с
постоянным темпом изменения
,
поскольку
На практике модель естественного роста может быть применена только на начаьном этапе развития экономической системы, в течение ограниченного промежутка времени, поскольку (как это следует из (4) и рис.2)с течением времени может принимать сколь угодно большие значения, что не может не сказаться на изменении цены ( в данной модели она предполагалась постоянной).