
Отчет о домашней работе №3
по дисциплине «Компьютерные технологии в приборостроении »
Вариант 2
Выполнил:
студент 2 курса
дневного отделения
факультет ПР напр.200100
группа ПР1-1101
Воронков В.Л.
Преподаватель:
Пышный В.М.
Москва - 2013
Таблица 1 – передаточные функции
№ вар |
№ схемы |
W1 |
W2 |
W3 |
W4 |
W5 |
2 |
2 |
|
|
|
|
|
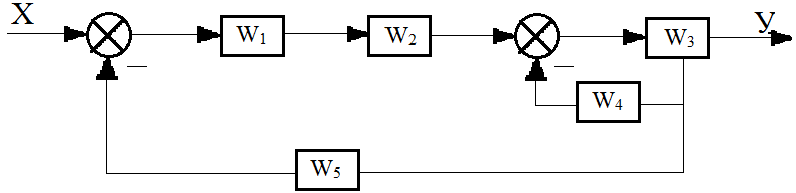
Рисунок 1 – структурная схема
Выполнение в среде Matlab
>> n1=[1]
>> d1=[0.64 2 1]
>> f1=tf(n1,d1)
Transfer function:
1
------------------
0.64 s^2 + 2 s + 1
>> n2=[1]
>> d2=[2 1]
>> f2=tf(n2,d2)
Transfer function:
1
-------
2 s + 1
>> n3=[1]
>> d3=[0.2 1 0]
>> f3=tf(n3,d3)
Transfer function:
1
-----------
0.2 s^2 + s
>> n4=[1]
>> d4=[0.2 0]
>> f4=tf(n4,d4)
Transfer function:
1
-----
0.2 s
>> n5=[1]
>> d5=[2 1]
>> f5=tf(n5,d5)
Transfer function:
1
-------
2 s + 1
>> f12=f1*f2
>> f34=f3/(1+(f3*f4))
>> f1234=f12+f34
>> f12345=f1234/(1+(f1234*f5))
Transfer function:
0.001049 s^15 + 0.02402 s^14 + 0.2286 s^13 + 1.203 s^12 + 4.061 s^11 + 10.15 s^10 + 20.86 s^9 + 34.34 s^8 + 40.94 s^7 + 35.73 s^6 + 27.6 s^5 + 17.56 s^4 + 6.6 s^3 + s^2
----------------------------------------------------------------------------------------------------
0.0002097 s^17 + 0.00582 s^16 + 0.06879 s^15 + 0.4633 s^14 + 2.066 s^13 + 6.969 s^12 + 19.55 s^11 + 45.71 s^10 + 86.98 s^9 + 138.4 s^8 + 183.4 s^7 + 181.8 s^6 + 122.3 s^5 + 54.08 s^4 + 15 s^3 + 2 s^2
>> [n6,d6]=tfdata( f12345, 'v' )
n6 =
Columns 1 through 11
0 0 0.0010 0.0240 0.2286 1.2032 4.0615 10.1466 20.8613 34.3384 40.9386
Columns 12 through 18
35.7280 27.6000 17.5600 6.6000 1.0000 0 0
d6 =
Columns 1 through 11
0.0002 0.0058 0.0688 0.4633 2.0660 6.9693 19.5523 45.7069 86.9759 138.4444 183.4000
Columns 12 through 18
181.8448 122.2720 54.0800 15.0000 2.0000 0 0
>> z = zero ( f12345 )
z =
0
0
-5.7549
-5.0000 + 0.0000i
-5.0000 - 0.0000i
0.3774 + 2.0498i
0.3774 - 2.0498i
-2.5000
-2.1270 + 0.7975i
-2.1270 - 0.7975i
0.2363 + 0.8374i
0.2363 - 0.8374i
-0.6250
-0.5000
-0.5000
>> p = pole ( f12345 )
p =
0
0
-5.8190
-5.7549
-5.0000 + 0.0000i
-5.0000 - 0.0000i
0.3882 + 2.1357i
0.3882 - 2.1357i
0.3774 + 2.0498i
0.3774 - 2.0498i
-2.4476
-2.5000
-1.1823
-0.2263 + 0.4415i
-0.2263 - 0.4415i
-0.6250
-0.5000
>> k = dcgain ( f12345 )
k =
0.5000
>> b = bandwidth ( f12345 )
b =
0.6425
>> f_ss = ss ( f12345 )
a =
x1 x2 x3 x4 x5 x6 x7 x8 x9
x1 -27.75 -20.5 -8.63 -2.405 -1.014 -0.7113 -0.8314 -0.791 -0.6296
x2 16 0 0 0 0 0 0 0 0
x3 0 16 0 0 0 0 0 0 0
x4 0 0 16 0 0 0 0 0 0
x5 0 0 0 8 0 0 0 0 0
x6 0 0 0 0 4 0 0 0 0
x7 0 0 0 0 0 2 0 0 0
x8 0 0 0 0 0 0 2 0 0
x9 0 0 0 0 0 0 0 2 0
x10 0 0 0 0 0 0 0 0 2
x11 0 0 0 0 0 0 0 0 0
x12 0 0 0 0 0 0 0 0 0
x13 0 0 0 0 0 0 0 0 0
x14 0 0 0 0 0 0 0 0 0
x15 0 0 0 0 0 0 0 0 0
x16 0 0 0 0 0 0 0 0 0
x17 0 0 0 0 0 0 0 0 0
x10 x11 x12 x13 x14 x15 x16 x17
x1 -0.417 -0.4135 -0.278 -0.2459 -0.1364 -0.07276 0 0
x2 0 0 0 0 0 0 0 0
x3 0 0 0 0 0 0 0 0
x4 0 0 0 0 0 0 0 0
x5 0 0 0 0 0 0 0 0
x6 0 0 0 0 0 0 0 0
x7 0 0 0 0 0 0 0 0
x8 0 0 0 0 0 0 0 0
x9 0 0 0 0 0 0 0 0
x10 0 0 0 0 0 0 0 0
x11 1 0 0 0 0 0 0 0
x12 0 1 0 0 0 0 0 0
x13 0 0 0.5 0 0 0 0 0
x14 0 0 0 0.5 0 0 0 0
x15 0 0 0 0 0.25 0 0 0
x16 0 0 0 0 0 5.96e-008 0 0
x17 0 0 0 0 0 0 5.96e-008 0
b =
u1
x1 2
x2 0
x3 0
x4 0
x5 0
x6 0
x7 0
x8 0
x9 0
x10 0
x11 0
x12 0
x13 0
x14 0
x15 0
x16 0
x17 0
c =
x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11
y1 0 0.1563 0.2237 0.1331 0.08755 0.07388 0.09228 0.09487 0.07808 0.04654 0.04062
x12 x13 x14 x15 x16 x17
y1 0.03138 0.03993 0.03001 0.01819 0 0
d =
u1
y1 0
Continuous-time model.
>> f_ss.d = 1
a =
x1 x2 x3 x4 x5 x6 x7 x8 x9
x1 -27.75 -20.5 -8.63 -2.405 -1.014 -0.7113 -0.8314 -0.791 -0.6296
x2 16 0 0 0 0 0 0 0 0
x3 0 16 0 0 0 0 0 0 0
x4 0 0 16 0 0 0 0 0 0
x5 0 0 0 8 0 0 0 0 0
x6 0 0 0 0 4 0 0 0 0
x7 0 0 0 0 0 2 0 0 0
x8 0 0 0 0 0 0 2 0 0
x9 0 0 0 0 0 0 0 2 0
x10 0 0 0 0 0 0 0 0 2
x11 0 0 0 0 0 0 0 0 0
x12 0 0 0 0 0 0 0 0 0
x13 0 0 0 0 0 0 0 0 0
x14 0 0 0 0 0 0 0 0 0
x15 0 0 0 0 0 0 0 0 0
x16 0 0 0 0 0 0 0 0 0
x17 0 0 0 0 0 0 0 0 0
x10 x11 x12 x13 x14 x15 x16 x17
x1 -0.417 -0.4135 -0.278 -0.2459 -0.1364 -0.07276 0 0
x2 0 0 0 0 0 0 0 0
x3 0 0 0 0 0 0 0 0
x4 0 0 0 0 0 0 0 0
x5 0 0 0 0 0 0 0 0
x6 0 0 0 0 0 0 0 0
x7 0 0 0 0 0 0 0 0
x8 0 0 0 0 0 0 0 0
x9 0 0 0 0 0 0 0 0
x10 0 0 0 0 0 0 0 0
x11 1 0 0 0 0 0 0 0
x12 0 1 0 0 0 0 0 0
x13 0 0 0.5 0 0 0 0 0
x14 0 0 0 0.5 0 0 0 0
x15 0 0 0 0 0.25 0 0 0
x16 0 0 0 0 0 5.96e-008 0 0
x17 0 0 0 0 0 0 5.96e-008 0
b =
u1
x1 2
x2 0
x3 0
x4 0
x5 0
x6 0
x7 0
x8 0
x9 0
x10 0
x11 0
x12 0
x13 0
x14 0
x15 0
x16 0
x17 0
c =
x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11
y1 0 0.1563 0.2237 0.1331 0.08755 0.07388 0.09228 0.09487 0.07808 0.04654 0.04062
x12 x13 x14 x15 x16 x17
y1 0.03138 0.03993 0.03001 0.01819 0 0
d =
u1
y1 1
Continuous-time model.
>> k1 = dcgain ( f_ss )
k1 = 1.5000
>> f_zp = zpk ( f12345 )
Zero/pole/gain:
5 s^2 (s+5.755) (s+5)^2 (s+2.5) (s+0.625) (s+0.5)^2 (s^2 + 4.254s + 5.16) (s^2 - 0.4727s + 0.757) (s^2 - 0.7549s + 4.344)
----------------------------------------------------------------------------------------------------
s^2 (s+5.819) (s+5.755) (s+5)^2 (s+2.5) (s+2.448) (s+1.182) (s+0.625) (s+0.5) (s^2 + 0.4526s + 0.2462) (s^2 - 0.7549s + 4.344) (s^2 - 0.7764s + 4.712)
>> who
Your variables are:
b d3 d6 f1234 f3 f5 k n2 n5 z
d1 d4 f1 f12345 f34 f_ss k1 n3 n6
d2 d5 f12 f2 f4 f_zp n1 n4 p
>> whos
Name Size Bytes Class
b 1x1 8 double array
d1 1x3 24 double array
d2 1x2 16 double array
d3 1x3 24 double array
d4 1x2 16 double array
d5 1x2 16 double array
d6 1x18 144 double array
f1 1x1 2190 tf object
f12 1x1 2206 tf object
f1234 1x1 2286 tf object
f12345 1x1 2430 tf object
f2 1x1 2174 tf object
f3 1x1 2190 tf object
f34 1x1 2238 tf object
f4 1x1 2174 tf object
f5 1x1 2174 tf object
f_ss 1x1 6244 ss object
f_zp 1x1 2920 zpk object
k 1x1 8 double array
k1 1x1 8 double array
n1 1x1 8 double array
n2 1x1 8 double array
n3 1x1 8 double array
n4 1x1 8 double array
n5 1x1 8 double array
n6 1x18 144 double array
p 17x1 272 double array (complex)
z 15x1 240 double array (complex)
Grand total is 846 elements using 30186 bytes
>> pzmap ( f12345 )
>> [wc,ksi,p] = damp ( f12345 )
wc =
0
0
0.4961
0.4961
0.5000
0.6250
1.1823
2.0843
2.0843
2.1707
2.1707
2.4476
2.5000
5.0000
5.0000
5.7549
5.8190
ksi =
-1.0000
-1.0000
0.4561
0.4561
1.0000
1.0000
1.0000
-0.1811
-0.1811
-0.1788
-0.1788
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
p =
0
0
-0.2263 + 0.4415i
-0.2263 - 0.4415i
-0.5000
-0.6250
-1.1823
0.3774 + 2.0498i
0.3774 - 2.0498i
0.3882 + 2.1357i
0.3882 - 2.1357i
-2.4476
-2.5000
-5.0000 + 0.0000i
-5.0000 - 0.0000i
-5.7549
-5.8190
>> ltiview
>> print -dmeta
>> w = logspace(-1, 2, 100);
>> r = freqresp ( f12345, w );
>> r = r(:);
>> semilogx ( w, abs(r) )
>> print -dmeta
>> [u,t] = gensig('square',4);
>> lsim (f12345, u, t)
>> print -dmeta
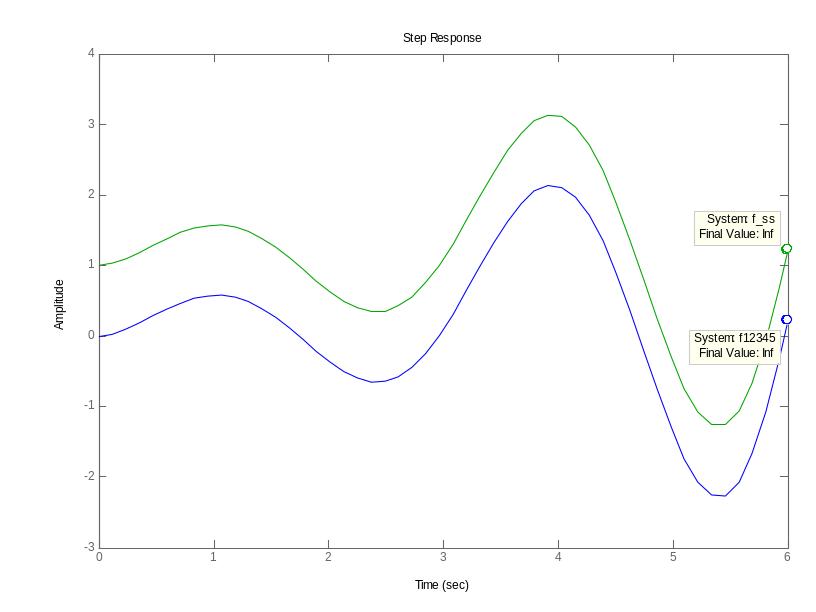
Рисунок 2 – переходные характеристики систем.
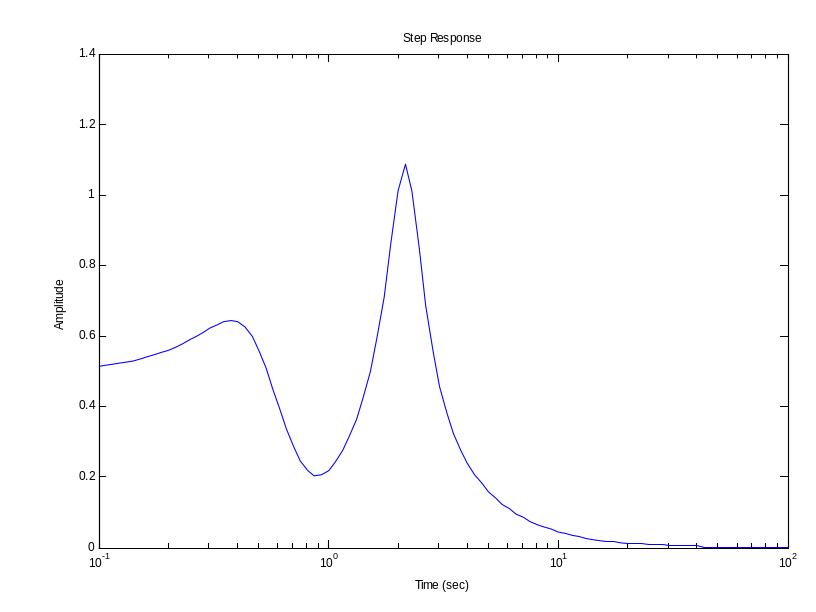
Рисунок 3 – частотная характеристика
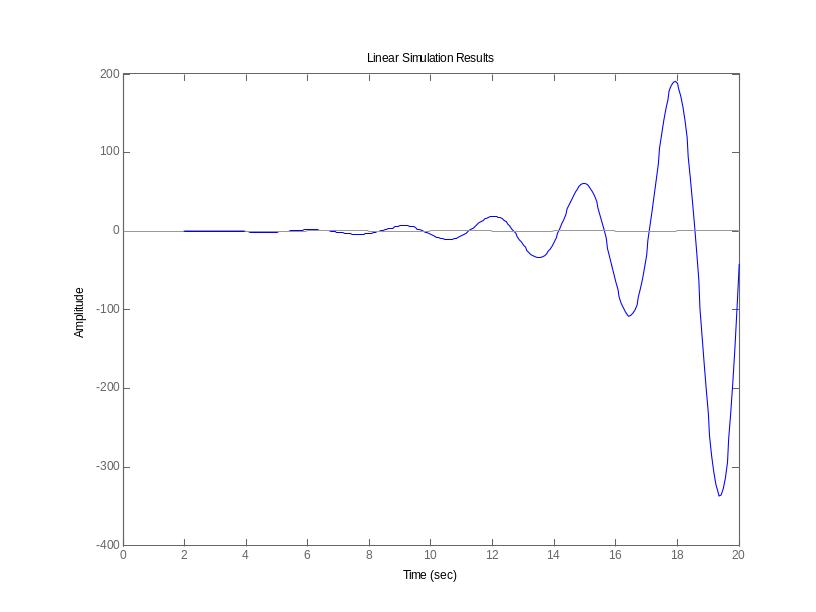
Рисунок 4 – сигнал выхода системы f при данном входе.
