МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ

Отчет о домашней работе №1

по дисциплине «Компьютерные технологии в приборостроении »

Вариант 2

Выполнил:

студент 2 курса

дневного отделения

факультет ПР напр.200100

группа ПР1-1101

Воронков В.Л.

Преподаватель:

Пышный В.М.

Москва - 2013

Задание №1

Решить систему линейных алгебраических уравнений

^0.63x₁^+x₂^+0.11x₃^+0.34x₄^=2.08

^0.17x₁^+1.18x₂^-0.45x₃^+0.11x₄^=0.17

0.31x₁-0.15x₂+1.17x₃-2.35x₄=1.28

0.58x₁+0.21x₂-3.45x₃-1.18x₄=0.05

>> A=[0.63 1 0.11 0.34; 0.17 1.18 -0.45 0.11; 0.31 -0.15 1.17 -2.35; 0.58 0.21 -3.45 -1.18]

>> B=[2.08; 0.17; 1.28; 0.05]

>> X=A\B

X =

3.4045

-0.1736

0.4924

0.1606

Задание №3

Вычислить интеграл:

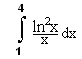
Интегрирование методом трапеций:

>> x = 1:1/100:4; y = log(x);

>> I = trapz(x, y)

I = 2.5452

Интегрирование методом квадратур:

>> [I, cnt] = quad('log', 1, 4)

I = 2.5452

cnt = 21

Задание №4

Таблица 1 - Задание для интерполяции и аппроксимации данных

x	2.0	2.1	2.2	2.3	2.4	2.5	2.6	2.7	2.8	2.9
y(x)	4,62·10-5	-0,44776	-0,8717	-1,2269	-1,4733	-1,5811	-1,5335	-1,3294	-0,9836	-0,5263

Выполнить кубическую интерполяция функции одной переменной:

>> x = 2:.1:2.9;

>> y=[0.0000462 -0.44776 -0.87178 -1.2269 -1.47335 -1.58114 -1.53356 -1.3294 -0.98363 -0.52634]

>> xi = 2:.05:3;

>> yi = icubic(x, y, xi);

>> plot(x, y, 'o', xi, yi, 'g'), grid

Рисунок 1 - Результат кубической интерполяции

Задание №5

Выполнить интерполяцию функции кубическим сплайном:

>> x = 2:.1:2.9;

>> y=[0.0000462 -0.44776 -0.87178 -1.2269 -1.47335 -1.58114 -1.53356 -1.3294 -0.98363 -0.52634];

>> xi = 2:.05:3;

>> yi = spline(x, y, xi);

>> plot(x, y, 'o', xi, yi, 'g'), grid

Рисунок 2 - Результат интерполяции кубическим сплайном

Задание №6

Выполнить одномерную табличную интерполяцию:

>> x = 2:.1:2.9;

>> y=[0.0000462 -0.44776 -0.87178 -1.2269 -1.47335 -1.58114 -1.53356 -1.3294 -0.98363 -0.52634];

>> xi = 2:.05:3;

>> yi = interp1(x, y, xi);

>> plot(x, y, 'o', xi, yi, 'g'), hold on

>> yi = interp1(x, y, xi, 'spline' );

>> plot(x, y, 'ob', xi, yi, 'm'), grid, hold off

Рисунок 3 - Результат одномерной табличной интерполяции

Задание №7

Выполнить аппроксимацию табличных данных на основе быстрого преобразования Фурье:

>> x = 2:.1:2.9;

y=[0.0000462 -0.44776 -0.87178 -1.2269 -1.47335 -1.58114 -1.53356 -1.3294 -0.98363 -0.52634];

xp = 2:0.1:3;

>> yp = interpft(y, 11);

>> xt = 2:0.01:3;

>> yt = interpft(y, 101);

>> plot(xt, yt, 'r'), hold on, plot(x, y, 'ob', xp, yp)

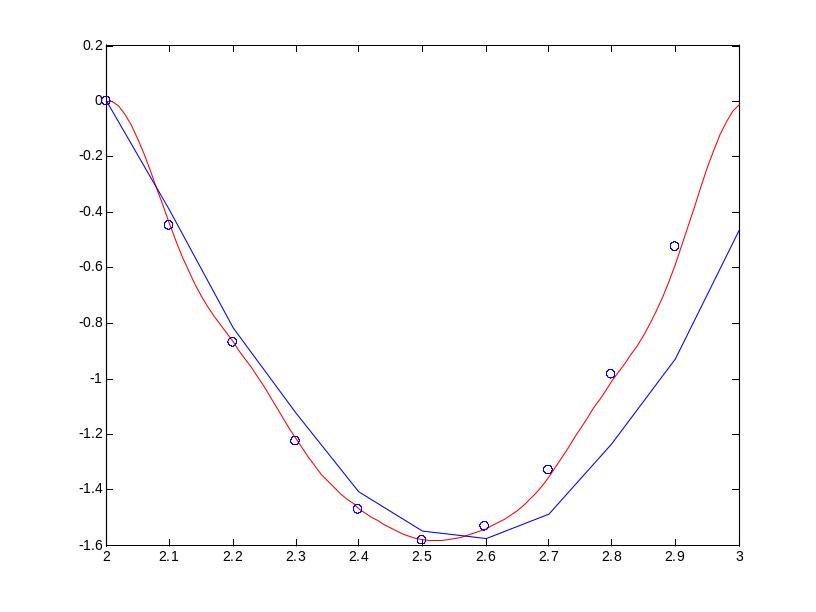
Рисунок 4 - Результат аппроксимации функции на основе преобразования Фурье

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ

Отчет о домашней работе №2

по дисциплине «Компьютерные технологии в приборостроении »

Вариант 2

Выполнил:

студент 2 курса

дневного отделения

факультет ПР напр.200100

группа ПР1-1101

Воронков В.Л.

Преподаватель:

Пышный В.М.

Москва - 2013

Задание №1

Вычислить символьными методами предел функции:

>> syms k

>> y1=(2^k)*((-1)^k)/(3*k+1)

>> limit(y1,6)

ans = 64/19

Задание №2

Решить символьными методами алгебраическое уравнение:

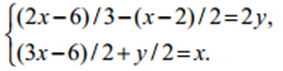
>> y=(((2*x-6)/3)-((x-2)/2))/2;

>> y=(x-((3*x-6)/2))*2;

>> S=solve(y,x)

S = 6

Задание №3

Произвести дифференцирование функции в символьном виде , кроме того к указанной функции применить 3-х кратное дифференцирование.

>> syms x

>> y6=((log(x))^2)/x;

>> diff(y6)

ans = 2*log(x)/x^2-log(x)^2/x^2

>> diff(y6,3)

ans =-12/x^4+22*log(x)/x^4-6*log(x)^2/x^4

Задание №4

Решить в символьном виде дифференциальное уравнение

y=ln(t)·cos(y/3)

>> y1=dsolve('Dy=log(t)','y(0)=0')

y1 = t*log(t)-t

>> ezplot(y1,[1,2]), grid, title('Диф.уравнение')

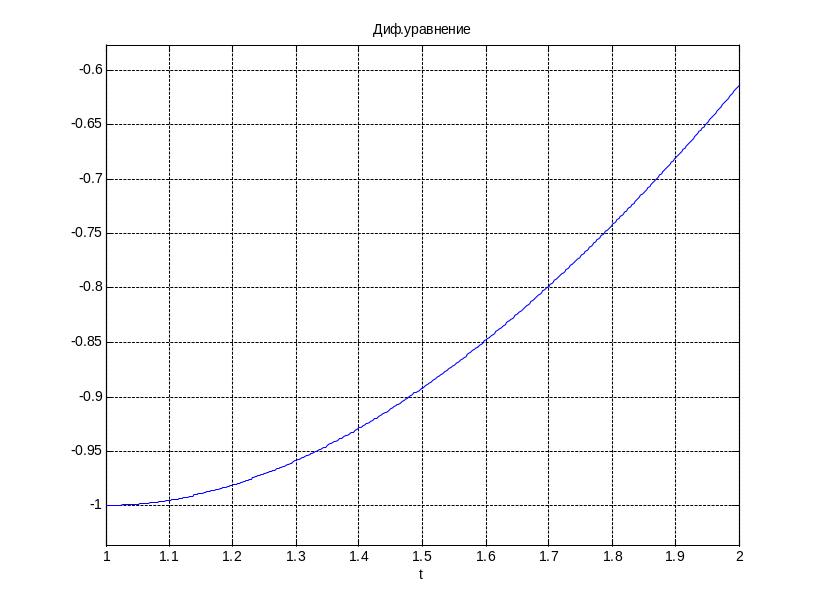
Рисунок 1 – результат решения дифференциального уравнения

Задание №5

Вычислить в символьном виде неопределенный и определенный интегралы:

>> syms x

>> int(((log(x))^2)/x)

ans = 1/3*log(x)^3

>> y7=int(((log(x))^2)/x,1,4)

>> vpa(y7,4)

ans = .8881

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ