2.3.Определение числа коэффициентов, необходимых для анализа изображения

Для анализа изображений по их Фурье‑образам необходимо определить достаточное для анализа количество коэффициентов. Это позволит сократить время анализа. Ниже приводятся примеры описания простых изображений посредством коэффициентов ряда Фурье.

1. Описание одиночной точки на черном фоне

Воспользовавшись зависимостями (17) и (18) можно получить следующие выражения: , (29)

, (30)

, (31)

, (32)

. (33)

Из совокупности зависимостей (29) – (33) можно выразить координаты x и y, описывающие одиночную точку на черном фоне:

, (34)

. (35)

Как видно из зависимостей (34) – (35), одиночная точка на черном фоне описывается 3‑мя коэффициентами ряда Фурье. Из этого следует, что для уменьшения числа коэффициентов ряда Фурье, необходимых для анализа изображения, следует проводить контрастирование исходного изображения.

2. Описание линии по горизонтали, состоящей из двух точек, на черном фоне Такое изображение согласно (5) и (6) имеет следующее описание:

, (36)

, (37)

(38)

, (39)

, (40)

где и – координаты точек линии.

Из выражений (24) – (28) следует, что координаты искомого объекта могут быть найдены как:

, (41)

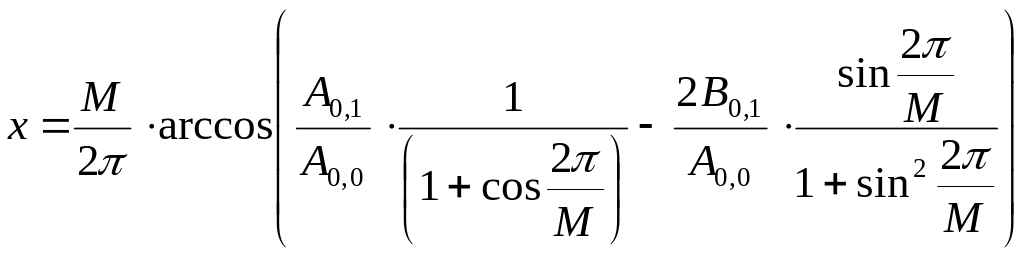. (42)

Как видно из совокупности (41) – (42) линия по горизонтали, состоящая из двух точек, описывается четырьмя коэффициентами ряда Фурье.

Для проверки правильности нахождения Фурье‑образа необходимо осуществить восстановление исходного изображения путем обратного преобразования Фурье, которое осуществляется согласно следующей зависимости:

(43)

Корреляционный анализ радиолокационного и моделируемого изображений целесообразно осуществлять на основе их Фурье‑образов. Так корреляционная функция Фурье‑образов радиолокационного и моделируемого изображений примет вид:

, (44)

, (45)

где – корреляционная функция радиолокационного и моделируемого изображений по коэффициенту ряда Фурье (т.е. по косинусному ряду);

– корреляционная функция радиолокационного и моделируемого изображений по коэффициенту ряда Фурье (т.е. по синусному ряду);

и – коэффициенты ряда Фурье для радиолокационного изображения;

и – коэффициенты ряда Фурье для моделируемого изображения;

– размер сравниваемых изображений.

Алгоритм нахождения корреляционной функции при совмещении радиолокационного и моделируемого изображений, основанный на вычислении зависимостей (44) и (45) представлен на рисунке 5.

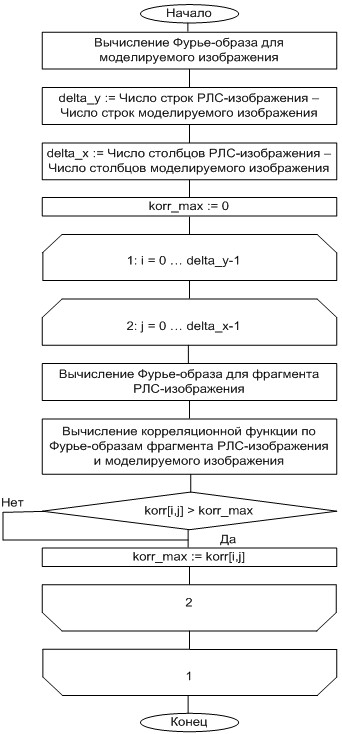
Рисунок 5 – Алгоритм нахождения корреляционной функции при совмещении радиолокационного и моделируемого изображений

Рассмотрим выражение для дискретного преобразования Фурье:

(46)

ДПФ N отсчетам сигнала s(n), n=0..N-1(в общем случае комплексным) ставит в соответствие N комплексных отсчетов спектра S(k), k=0..N-1, причем для вычисления одного спектрального отсчета требуется N операций комплексного умножения и сложения. Таким образом вычислительная сложность алгоритма ДПФ составляет N2 комплексных умножений и сложений. При этом можно заметить что если одно ДПФ на N точек (отсчетов) заменить вычислением двух ДПФ по N/2 точек, то это приведет к уменьшению количества операций в 2 раза.