4. Еркін түсу үдеуі, оның қалыпты мәні

Жер бетіндегі әрбір денеге немесе әрбір массаға бүкіләлемдік тартылыс заңына сәйкес тартылыс күші және Жер айналуымен байланысты, центрге тартқыш күш әсер етеді. Осы екі күштің тең әсерлі күші анықтау пунктіндегі g еркін түсу үдеуіне байланысты болатын, см/с² (галмен) ауырлық күші табылады.Жердегі еркін түсу үдеуінің орташа мәні шамамен 981 см/с² тең.

Еркін түсу үдеуі жердің әрбір нүктесінде өзгеруі мүмкін.

1.5 - суретте g ауырлық күшінің векторы тіктеуіш сызығының бағытына сәйкес келеді. Еркін түсу үдеуінің шамасы және g векторның бағыты әрбір нүктеде әр түрлі және М нүктесінің ендігіне және берілген нүктенің айналасындағы Жерде массалардың таралуына байланысты болады.

1.5-сурет - Ауырлық күші g: F-тартылу күші, P-центрден тепкіш күш

М нүктесінің меридиан бойынша экватордан полюстерге жылжуы кезінде еркін түсу үдеуінің өзгеруі эллипсоид бетінде еркін түсу үдеуінің қалыпты таралуы формуласынан анықталады:

(1.8)

g_э, және шамаларын Жер бетінде еркін түсу үдеуін көптеген өлшеулері нәтижесінде анықтайды. (1.8) формуласымен анықталған мәндерін қалыпты мәндер деп атайды. Экватордан полюсқа қарай жылжыған кездегі еркін түсу үдеуінің толық өзгерісі 5,2 см/с² тең, яғни, g орташа мәнінің 0,6% тең. Бұл полюста 1 кг болатын кір тасы экваторда 994г болады.

Жер қабатының бір қалыпсыз тығыздығымен байланысты болатын, еркін түсу үдеуінің өзгерістері өлшенген g мәні қалыпты мәнінен ауытқуын жалпылайды. Берілген нүктедегі g– ауытқулары ауырлық күштерінің аномалиясы деп аталады.

Ауырлық күштерінің аномалиясы Жер фигурасы туралы, жер қабатының құрылымы туралы және онда пайдалы қазбалардың таралуы туралы мәлімет береді.

Еркін түсу үдеуі кеңістікте де өзгереді, өйткені материалды нүкте биіктік бойынша жылжиды. Жер массалары центрінен алыстаған кезде еркін түсу үдеуі азаяды, жақындаған кезде келесі шамаға көбейеді:

(1.9)

Бұл заң Жердің физикалық бетінде өлшенген еркін түсу үдеуінің шамасын референц-эллипсоид бетіне келтіруге (редукцивтеуге) және аномалияны есептеп шығаруға мүмкіндік береді. Одан басқа, редуцивтеген кезде аралық қабаттың тартылуының әсерін және басқа да факторларды есепке алады. Осылайша, аномалияларды есептеу үшін еркін түсу үдеуінің өлшенген шамасы эллипсоид бетіне келтірілу (редуцивтелу) қажет.

Теңдестірілген жазықтықта оның әрбір нүктесінде ауырлық күші оның нормаліне тіктеуіш сызығы бойынша бағытталатындығын көрсеткен болатынбыз. Материалды нүкте биіктік бойынша бір теңдестірілген жазықтықтан екіншісіне тіктеуіш сызығы бойынша – шамасына жылжу үшін еркін түсу үдеуінің биіктік өзгеру шамасына көбейтіндісіне тең болатын жұмыс жасалу қажет

(1.10)

шамасы

(1.11)

мұндағы – бір-біріне жақын орналасқан екі теңдестірілген жазықтықтарға сәйкес келетін, ауырлық күшінің потенциалдары.

шамасы бір-біріне жақын орналасқан екі теңдестірілген жазықтықтар үшін тұрақты, яғни, материалды нүкте бір теңдестірілген жазықтықтан екіншісіне өткен кезде осы жазықтықтардың кез-келген нүктесінде бірдей жұмыс жасалу қажет (1.6- сурет).

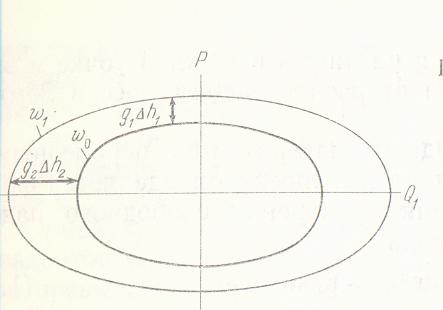
1.6-сурет - Теңдестірілген жазықтықтар арасындағы қашықтық

10. формуласынан

(1.12)

теңдестірілген жазықтықтар арасындағы қашықтық тұрақты шамасында әр түрлі нүктелерде әр түрлі және еркін түсу үдеуінің шамасына байланысты.

Егер нүкте теңдестірілген жазықтықтың бойымен қозғалатын болса, онда ешқандай жұмыс жасалмайтындығын , көрсету керек.

Осының нәтижесінде жұмыс істеп тұрған ауырлық күшінің бағыты берілген жазықтыққа перпендикуляр, бұл жазықтық бойынша сұйық жүрмейді, яғни, теңдестірілген жазықтық теңдесу жазықтығы болып табылады.