1.3 Жердің физикалық бетіндегі нүктелерді референц эллипсоидқа түсіру

Жердің физикалық бетіндегі жасалған, өлшеу нәтижелерін математикалық өңдеу мүмкіндігін қаматамасыз ету мақсатымен, горизонталь бұрыштар және сызықтар ұзындықтарын эллипсоид бетіне редуцивтеу арқылы жасайды (нормаль бойынша проекциялайды).

Инженерлік – геодезиялық жұмыстарда көбіне Жер бетін, жер эллипсоидына тең болатын, шар ретінде қабылдайды. Мұндай шардың радиусы келесі қатынастан анықталады:

(1.1.)

Красовский эллипсоды үшін R=6371,11км

Мысалы, егер Жер бетінде S қашықтығы өлшенген болса, онда түзету енгізу жолымен, референц - эллипсоид бетіндегі әрі қарай қолданылатын, S₀ қашықтығына өтеді.

Геодезиялық пунктта теодолиттің вертикаль осі тіктеуіш сызығымен сәйкес келуіне байланысты, өлшенген горизонталь бұрыш эллипсоид бетіне редуцивтеген кезде тіктеуіш сызықтарының нормальдан ауытқуы шамасына түзетілу керек. Пайдалы қазбаларды өңдеу жүріп жатқан аномальды аймақтарда бұл түзетудің шамасы 10^// және одан да үлкен шаманы құрауы мүмкін.

Өлшенетін горизонталь бұрышқа эллипсоид бетіне редуцивтеген кезде «бақыланатын пункттің биіктігіне» де түзету енгізілу керек. Бұл түзету, Жердің физикалық бетінде жатқан нүктеден және осы нүктенің эллипсоид бетіндегі проекциядан өтетін, коллимациондық жазықтықтың сәйкес келмеуі салдарынан болады. Ол таулы аймақтарда үлкен болуы мүмкін және оны 1 және 2 классты триангуляцияда есепке алады.

Референц эллипсоид бетіне қандай да бір геодезиялық тордың (триангуляциондық, полигонометриялық немесе трилатерациялық) барлық өлшенген элементтерін келтіру нәтижесінде, осы эллипсоидтың бетінде құрылғандай болатын тор шығады. Тордың басқа математикалық өңдеуін оның пункктарының координаталарының мәндерін есептеуді референц эллипсоидтың бетінде жүргізуге болады. Бірақ өңдеуді жеңілдету үшін және соңғы нәтижелерді қолдану мүмкіндігі үшін кейіннен референц эллипсоид бетінен шарға және жазықтыққа өтуді орындайды.

Инженерлік тәжірибенің көптеген жағдайларында, жеке жағдайларда жергілікті жердің кішкене учаскесінің планын жасаған кезде Жердің сфералық бетін жазықтық ретінде қабылдау мүмкіндігі пайда болады.

Жер бетінің көптеген бөліктерін жазықтыққа бейнелеу үшін, Жер бетінің нүктелерін жазықтыққа математикалық заңдар бойынша келтіруге мүмкіндік беретін, проекциялаудың көптеген тәсілдері қолданылады.

Жалпы жағдайда проекциялар қандай да бір шамалардың: бұрыштардың, сызықтар үзындықтарының, аудандардың, өзгеруіне алып келуі мүмкін. Геодезияда бұрыштар өзгермейтін проекциялар кеңінен қолданылады. Мұндай проекциялар конформды немесе теңбұрышты деп аталады. Мұндай проекциялардың қатарына Гаусс проекциясы жатады.

4. Астрономиялық және геодезиялық координаталар

Координаталар деп қатысты түрде санақ басы болып алынған, жазықтықта, кеңістікте, қандай да бір басқа бетте, сонымен қатар эллипсоид бетінде де, нүктелердің орнын анықтайтын, сызықтық және бұрыштық шамалар аталады.

Нүктелердің қатысты орны анықталатын сызықтар мен жазықтықтар сәйкесінше координат осьтері және координаттық жазықтықтар деп аталады.

Геодезияда негізгі координаталық жүйелер ретінде географиялық (геодезиялық және астрономиялық) және тік бұрышты координаталар жүйесі алынады.

1. B және L геодезиялық координаталар жүйесі. Геодезиялық өлшеулер нәтижесінде есептелген, эллипсоид бетіндегі нүктелер ендік В және бойлық L геодезиялық координаталар деп аталады.

Геодезиялық ендік деп берілген нүктеде эллипсоид жазықтығындағы Мn нормалімен және экватор жазықтығымен жасалған В бұрышы аталады.

Геодезиялық бойлық деп бастапқы меридиан жазықтығымен (PqQP₁) және М нүктесінің жазықтығынан (PMEP₁) жасалған екі жақты бұрышты атайды.

Солтүстік жарты шарда орналасқан нүктелер ендігі оң деп аталады, олар «с.е.» индексімен белгіленеді.

Оңтүстік жарты шарда орналасқан нүктелер ендігі теріс деп аталады, олар «о.е.» индексімен белгіленеді.

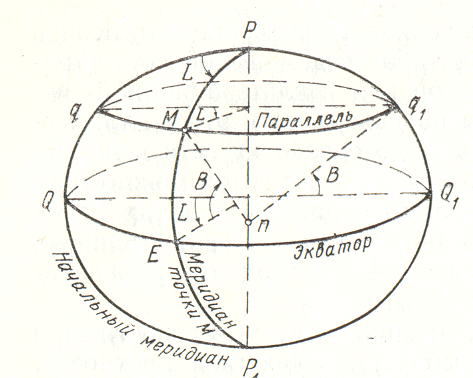
1.2-сурет - Геодезиялық координаталар жүйесі

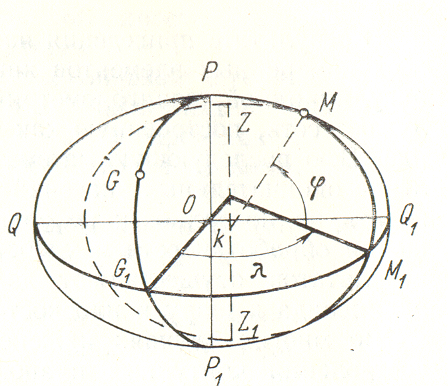
1.3-сурет - Астрономиялық координаталар жүйесі

Бойлықтар 0 ден 180⁰ дейін есептеледі (о ден 12һ дейін).

Бастапқы меридианнан шығыста орналасқан нүктелер бойлығы оң деп аталады, «ш.б.» индексімен белгіленеді.

Бастапқы меридианнан батыста орналасқан нүктелер бойлығы теріс деп аталады, «б.б.» индексімен белгіленеді.

Геодезиялық координаталар жүйесі эллипсоид бетіне жалпы болып табылады, оның меридиан және параллель түріндегі координаттық сызықтары бар.

2. φ, λ астрономиялық координаталары. Астрономиялық тәсілдермен яғни тіктеуіштің шырақтарын бақылау арқылы нәтижелері бойынша анықталатын ендігі φ және бойлығы λ астрономиялық координаталар деп аталады.

Нүктенің астрономиялық бойлығы деп, осы нүктеден өтетін Mk тіктеуіш сызығымен (геоид жазықтығына түскен нормальмен) және экватор жазықтығымен жасалынатын φ бұрышы аталады.

Асторономиялық бойлық деп берілген нүктенің бастапқы меридиан жазықтығымен (PGG₁P₁) және астрономиялық меридиан жазықтығымен (ZMM₁Z₁) жасалған λ екі жақты бұрышты атайды.

Астронромиялық координаталар геодезиялық сияқты есептелінеді.

Осылайша, геодезиялық ендік В және бойлық L жер эллипсоидының бетінде жатқан нүктенің орнын анықтайды және оның бетіне берілген нүктенің нормалімен байланысқан, ал φ және λ астрономиялық координаталары берілген нүктеде тіктеуіш сызығымен байланысқан.

Жер массаларының бір қалыпсыз таралуына байланысты, геоид бетінің қабылданған референц - эллипсоиды бетінен ауытқулары тіктеуіш сызықтары жалпы жағдайда эллипсоид нормалімен сәйкес келмейді, осы нүктедегі тіктеуіш сызығының ауытқуы деп аталатын, онымен и бұрышын құрайды. Тіктеуіш сызығының ауытқуын пайдалану ыңғайлы болу үшін, оны ендік бойыша – кси және бойлық бойынша - эта құрамдастары түрінде көрсетеді.

Сонымен астрономиялық және геодезиялық координаталар бір - бірімен келесі тәуелділікпен байланысқан:

(1.2)

(1.3)

Тіктеуіш сызығының ауытқуы КСРО - ның көптеген бөлігі үшін 3,0-3,5^// құрайды немесе сызықтық шамада 100м жуық, ал аномальды аймақтарда (әдетте тау - кен қазбалары аймақтарында) ауытқулар 10 - 20, кейде 40^// тең болуы мүмкін.

Асторономиялық координаталар жүйесінен геодезиялық координаталар жүйесіне ауысу үшін берілген нүктенің ζ және λ шамаларын білу керектігі анық.

«Географиялық координаталар» термині Жерді шар ретінде қабылдап, ал координаталарды астрономиялық бақылаулармен анықтаған заманда пайда болған, осы кезден геодезиялық және астрономиялық координаталарды теңдестірген. Ал геодезиялық және асрономиялық өлшеулердің дәлдігі жоғарлаған кезде, жер бетінің бір нүктесінің геодезиялық және астрономиялық координаталары арасындағы айырмашылық бар екендігі анықталған. Бірақ «географиялық координаталар» термині екі координаталар жүйелерінде де сақталып қалған.

Осылайша географиялық координаталар деп шар, эллипсоид, геоид жазықтығына, ал математикада кез - келген айналу бетіне, нормаль бағыттарымен анықталатын, нүктенің ендігі және бойлығы аталады.

Эллипсоидта және геоидта бағдарлаушы бұрыштар болып азимуттар табылады; геодезиялық (нақты) А және астрономиялық а.

А - геодезиялық азимут - бұл геодезиялық меридиан және эллипсоидқа нормаль арқылы өтетін, берілген бағыттың қалыпты қимасының жазықтығымен жасалған бұрыш.

А - астрономиялық азимут - бұл нүктенің астрономиялық жазық-тығымен және берілген бағыттың коллимациялық жазықтығымен (коллимациялық жазықтық тіктеуіш сызығы бойымен өтеді) жасалынған бұрыш.

Азимуттар меридианның солтүстік бағытынан сағат тілі бағытымен берілген бағытқа дейін 0 - ден 360⁰ - дейін есептеледі.

Кез - келген бағыттың геодезиялық азимутының берілген нүктенің тіктеуіш сызығының ауытқуы есесінен астрономиялық азимуттан, Лаплас түзетуі деп аталатын, (А-а) шамасына айырмашылығы болады.

(1.4)

Осы түзету жолымен астрономиялық азимутқа есептелген геодезиялық азимут Лаплас азимуты деп аталады:

(1.5)

Лаплас азимуттары – геодезиялық торлардағы тәуелсіз өлшеулер, оларды қолдану:

1) геодезиялық тордың жақтар бағдарлауының қажетті дәлдікпен қамтамасыз етуге;

2) триангуляцияда және полигонометрияда бұрыштық өлшеулердің сапасын қадағалауға, бұрыштық өлшеулердің жүйелік қатесінің әсерін төмендетуге; 3) геодезиялық құрылғылардың сапасын жоғарлатуға мүмкіндік береді.