3 Негізгі геодезиялық жұмыстар. Геодезиялық жүйе

Геодезиялық жүйе – бұл жер бетіндегі пункттердің жиынтығы, ол үшін қандай да бір координаталар жүйесінде координаталары белгілі болады.

Геодезиялық жүйелер үш түрге бөлінеді:

1. мемлекеттік геодезиялық тіректі жүйе;

2. біріктіру жүйелері;

3. түсіру жүйелері.

Геодезиялық жүйелер жалпыдан жекеге, жоғары дәлдікті жүйеден аз дәлдікті жүйеге қарай салынады.

Геодезиялық жүйелер триангуляция, трилатерация және полигонометрия әдістерімен салынады.

Әр түрлі масштабты түсірілімдерді жүргізу үшін әр түрлі тығыздықты геодезиялық жүйелер ќажет.

(3.1)

мұндағы S – үшбұрыштың бір жағының ұзындығы, км.

Сонымен 1:100000 және одан аз масштабты түсірілімді қамтамасыз ету үшін 50, 60 км² бір тірек қажет.

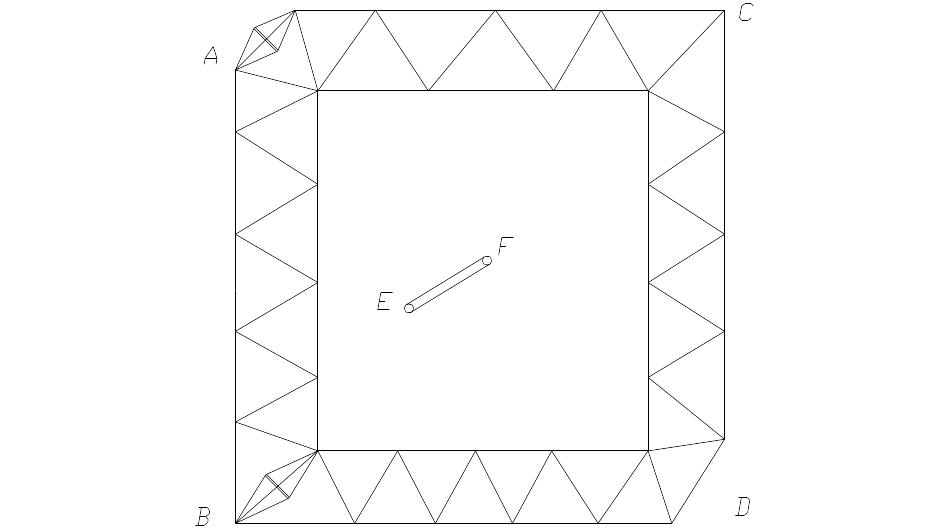
3.1 –сурет- Геодезиялық тор

Негізгі геодезиялық жұмыстарға геодезиялық торларды құруды және олардың элементтерін анықтаудың дәлдігін бағалаудың алдын алу жатқызады.

Геодезиялық тор деп жергілікті жерде, бір координаталар жүйесінде орны анықталған, бекітілген нүктелер (пункттар) жиынтығын атайды.

Жердің физикалық бетінде орналасқан, геодезиялық пункттар орны үш координат бойынша анықталады; В ендігімен, референц-эллипсоид бетіндегі L бойлығымен және пункттің эллипсоид бетімен, Н биіктігімен.

В және L координаталары пункттың пландық орнын анықтайды. Тәжірибелік мақсаттар үшін пункттің пландық орнын жазықтықта х және у координаталарымен , мысалы Гаусс проекциясында, анықтайды.

Н биіктігі оның геоид бетінен биіктік шамасының және геоидтың эллипсоидтан алшақтау шамасының қосынды ретінде келтіреді.

Жер бетінде пункттардың өзара орнын анықтаудың жалпы принципі келесідей.

Жергілікті жерде бір-бірімен байланысқан геометриялық фигураларды, әдетте үшбұрыштарды, орналастырады. Бұл фигуралардың төбелерін, олардың кейбір элементтері үздіксіз өлшеулер үшін ыңғайлы болатындай етіп таңдайды.

Үшбұрыштағы пункттардың пландық орнын анықтау үшін, мысалы, бір қабырғасын және екі бұрышты немесе екі қабырғасын және бір бұрышын өлшеу жеткілікті, қалған элементтерің аналитикалық түрде оңай есептеп шығаруға болады. Бірақ геодезиялық жұмыстар тәжірибесінде, геометриялық құрылыстардың барлық элемнттерін анықтауға қажетті өлшеулерден көп орындайды. Артық өлшеулерді геодезиялық торлар құрудың сапасын жоғарлату үшін, тексеру үшін және дәлдігін бағалау үшін жасайды.

Фигуралар төбесінің абсолютті биіктіктерін анықтау мақсатымен, не қабырғалар ұзындығын біле отыра вертикаль бұрыштарды өлшеу жолымен, не геометриялық нивелирлеу жолымен, сәйкес өсімшелерді (биіктіктер айырмашылығы) анықтайды, көршілес пункттердің биіктіктерінің айырмашылығын анықтайды.

Бірақ құрылған фигураларды бағдарлау, пландық орнын анықтау және барлық төбелердің биіктіктерін анықтау үшін бір қабырғаның азимутын (дирекциондық бұрышын), координаттарын (В,L немесе х және у) және фигуралар жүйесінің бір төбесінің абсолюттік биіктігін білу қажет. Пландық орынды анықтау және пункттердің биіктік қалпын анықтау тәсілдерінің бір-бірінен едәуір айырмашылығы бар екендігін есепке алу керек. Пландық орнынды анықтау және геодезиялық пукттердің биіктіктерін анықтау өлшеулері бөлек және көбінесе әр түрлі тіктеуішптермен жасалады.

Осылай тірек торын құрып, оның пункттарнына қатысты жергілікті жердің кез-келген нүктесінің орын анықтауға болады.

Өлшеулер түріне байланысты геодезиялық тор триангуляция, трилатерация, полигонометрия және олардың аралас тәсілдерінен құрылады. Соңғы кезде бір-бірінен алшақ жатқан пункттер орнын Жердің жасанды серіктерін бақылау арқылы анықтайтын болды.

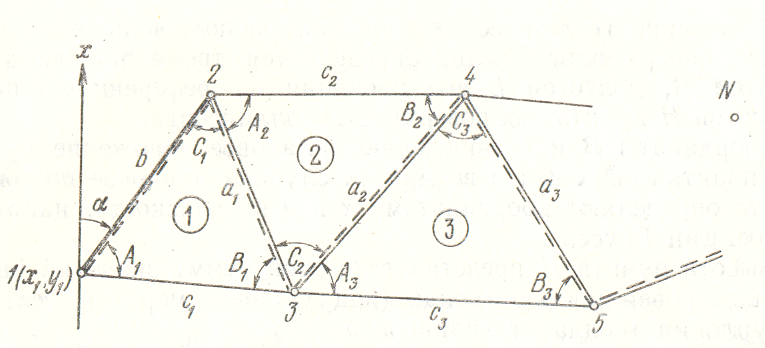
3.2 -сурет – Триангуляция үшбұрыштар қатары

Триангуляция – бұл жергілікті жерде, горизонтальді бұрыштарды және бір үшбұрыштың қабырғасының ұзындығы (қабырғалар бірнеше үшбұрышта өлшенуі мүмкін) анықталатын, бір біріне ұласқан үшбұрыштарды құру. Үшбұрыштарды өлшенген b қабырғасынан, бастапқысына қатысты біртіндеп шеше отырып (3.2-сурет), үшбұрыштар жүйеісінің барлық қабырғаларын анықтайды

(3.2)

Әрбір үшбұрышта оның қабырғаларын анықтайды

(3.3)

мұндағы

(3.4)

n нөмірлі үшбұрыш үшін анықталатын

(3.5)

мұндағы

(3.6)

Содан кейін бастапқы пункттың анықталған х₁, у₁ координаталары және белгілі қабырғаның (базистік жақтың) α дирекциондық бұрышы бойынша, мысалы, 1-2-3-4....N жүрісі бойынша геодезиялық тура есепті шешу арқылы, үшбұрыштар төбелерінің координаталарын есептейді.

Жергілікті жерде бекітілген және сәйкес белгіленген үшбұрұштар төбелері триангуляция пункттары деп аталады. Триангуляцияның өлшенген жағы базисті деп аталады, ал координаталары берілетін пункт триангуляцияның бастапқы пункты деп аталады.

Триангуляцияның жағын өлшеу мүмкін болмаған кейбәр жағдайларда жергілікті жерде базистік тор құрылады (3.3- сурет). Шығыс жағы деп аталатын, (1-2-3) торы үшбұрышының 1-2 жағының ұзындығы базистік торды өңдеуден аналитикалық түрде анықталады. Базистік тор әдетте,кіші АВ диагоналі немесе кіші қабырғасы өлшенетін, ромб түрінде болады.

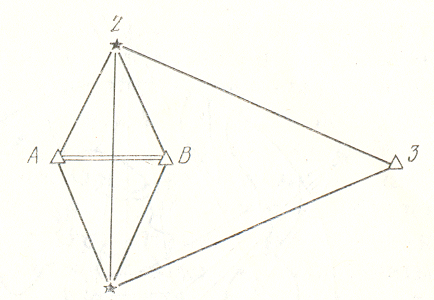
3.3-сурет- Базистік тор

Трилатериция – бұл жергілікті жерде, барлық қабырғалары өлшенетін, бір-біріне ұласқан геометриялық фигураларды (үшбұрыштар, төртбұрыштар және т.б.) құру.

Мысалы, тригонометрия формулаларымен үшбұрыштарды шеше отырып, дирекциондық бұрыштарды есептеуге қажетті, барлық горизонтальды бұрыштарды анықтайды,

(3.7)

немесе

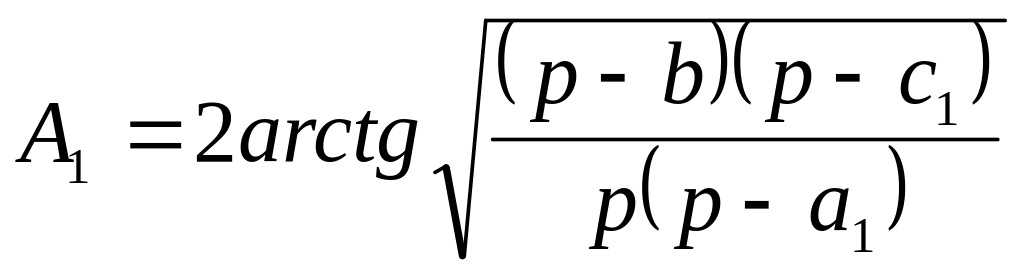(3.8)

мұндағы .

Трилатерация пункттерінің координаталарын (фигуралар төбелерін) триангуляциядағы әдіспен анықтайды.

Полигонометрия – бұл жергілікті жерде тұйықталмаған және тұйықталған сынық сызықтар жүйесін құру. Полигонометрияда барлық сызықтарды және екі көршілес сызықпен жасалынған горизонталь бұрыштарды өлшейді (3.4-сурет). Полигонометрияның теодолиттік жүрістен айырмашылығы горизонтальді бұрыштар және жақтар ұзындығы жоғары дәлдікпен анықталуында.

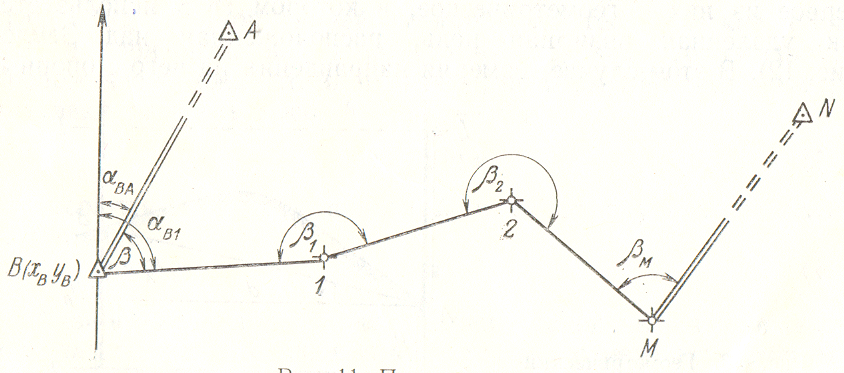
3.4-сурет. Полигонометрия

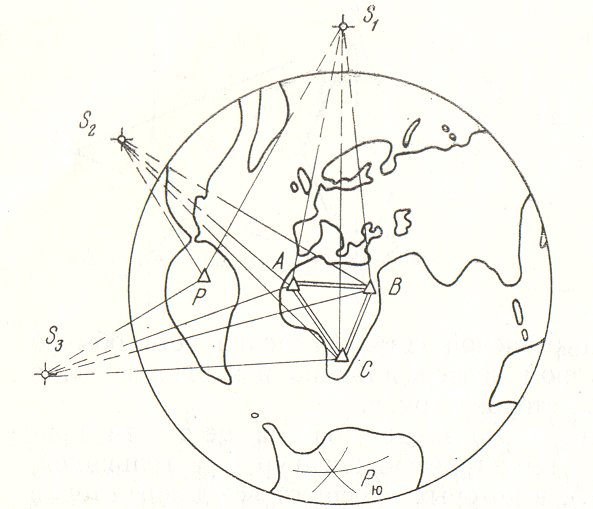
3.5-сурет. Спутниктік триангуляция

Полигометриялық жүрістің координаталарын бастапқы мәліметтерге (координаталар және дирекциондық бұрыштар) қатысты есептелген дирекциондық бұрыш және өлшенген сызықтырдың ұзындығы негізінде анықтайды.

Геодезиялық торды бағдарлаудың тексерісі мақсатымен Лаплас пукттарын анықтайды. Осы пункттарда астрономиялық бақылаулар нәтижелері бойынша ендікті, бойлықты және астрономиялық азимутты анықтайды, содан соң Лаплас түзетуін есепке алып геодезиялық азимутты есептейді.

Лаплас пункттары болып тринагуляцияның базистік жақтарының пункттары немесе бөлек полигонометриялық жүрістердің соңғы пунктары табылады.

Геодезиялық тор пункттарының координаталары Жердің жасанды серіктерін (ЖЖС) бақылау арқылы анықталуы мүмкін.

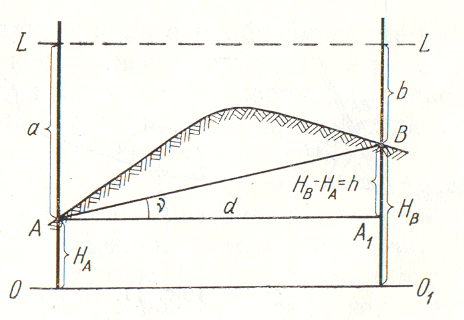
3.6-сурет -Нивелирлеудің геометриялық принципі

ЖЖС қолдану геодезияда екі түрлі бағытпен дамиды. Олардың біріншісі–геометриялық, мұнда ЖЖС, Жерден жоғары орналасқан, алыстатылған визирлік нысана ретінде қолданылады (3.6-сурет). Бұл жағдайда, (А,В,С) геодезиялық тірек пункттарынан оған дейінгі қашықтықты өлшей отырып, кеңістікте серіктің орнын (S₁,S₂,S₃) анықтайды. Дәл осы кезде анықталатын (Р) пункттан ЖЖС дейінгі қашықтықтарды өлшеп, аналитакалық түрде оның координаталарын алуға болады. Осылайша –бақылау кезінде ЖЖС орналу жерлерінде–төбелері Жерде және кеңістікте бола алатын, кеңістіктік үшбұрыштар жүйесі құрылуы мүмкін. Белгілі (АВ,ВС,СА) базистерді біле отырып, барлық кеңістіктік үшбұрыштарды шешуге, төбелері арасындағы қашықтықты есептеуге, содан кейін олардың координаталарын анықтауға болады. Бұл әдіс синхронды бақылау әдісі деп аталады. Онымен, бірнеше километрге дейін жететін, үлкен қашықтықтарды анықтауға болады. Әдіс, әр түрлі континеттерде құрылған геодезиялық торларды, біртұтас координатты жүйеге бірікртіруге мүмкіндік береді.

ЖЖС қолданудың екінші бағыты геодезияда динамикалық есепті шешуге негізделген. ЖЖС қозғалу теориясы негізінде серіктің орбитадағы орнын және оның кеңістіктегі координаталарын анықтауға болады. Мұндай тәсілді көбіне орбитальды деп атайды. Бұл тәсіл кеңістіктік ғарыштық триангуляция құру үшін қолданылу мүмкін.

Геодезиялық тордың биіктіктерін, екі принципті–геометриялық және физикалық– қолдануға негізделген, нивелирлеу арқылы анықтайды.

Нивелирлеудің геометриялық принципі горизотальді (геометриялық нивелрилеу) немесе еңісті (тригонометриялық нивелирлеу) сәулені қолдануға негізделген.

Геометриялық нивелирлеуде (3.6-сурет) А және В нүктелерінің абсолютты Н_А, Н_В биіктіктерінің айырмасы һ=Н_В-Н_А, горизонтальды сәуледен Жердің физикалық бетінің нүктелеріне дейінгі қашықтықтардың айырмасына тең

Һ=а-b (3.9)

Егер триангуляцияның немесе полигонометрияның геодезиялық пункттарында еңіс бұрыштары (АВ геодезиялық пункттарын қосатын түзу сызық және АА₁горизонтальді сызық арасын қосатын сызықтар расындағы бұрыш) өлшенген болса, онда пункттар арасындағы d аралығын біле отыра, тригонометрия формулаларымен биіктіктер айырмасын һ=Н_В-Н_А алады

(3.10)

Екі жағдайда да В пунктының абсолютты биіктігін келесі формула бойынша анықтайды

(3.11)

Нивелирлеудің физикалық әдістері, әр түрлі физикалық көрңнңстерде болатын, Жердің биіктігінің және сыртқы гравитациялық өрістерінің өзгерістері арасындағы байланысқа негізделген. Физикалық әдістерге жататындар: барометрлік, гидросатикалық механикалық нивелирлеу және геометриялық әдіс сияқты абсолютты биіктіктерді көршілес пункттардың биіктіктерінің айырмашылығын анықталатын басқа да тәсілдер.

Өлшеулер нәтижесін математикалық өңдеу геодезиялық торды құрудың қорытнды бөлімі болып табылады.

Алдын-ала есептеулерге далалық материалдарды тексеру, өлшенген бағыттарды пункттар центріне келтеру және бағыттарды Гаусс проекциясында жазықтыққа редуцивтеу жатады.

Теңдестіру емептерінің мақсаттары геометриялық шарттардың қиылыспаушылықтарын ануқтау жіне геодезиялық тор элемнттерінің жақын болатын мәндерін анықтау.

Геодезиялық торды құрудың дәлдігін бағалау мақсаттарға байланысты күрделі және жеңілдетілген тәсілдермен жасалуы мүмкін. Күрделі тәсілдер әр түрлі геодезиялық торларды теңестіру кезінде қолданылады. Дәлдікті бағалаудың жеңілдетілген тәсілдері торларды жобалған кезед кең қолданыс табады.

Соңғы есптеулерге каталогтарды құруға қажетті, берілгендерді алу және тексеру жатады. Жұмыстар каталогтарды құрумен аяқталады.