
- •Спасское Городище 2012
- •Введение
- •Список обозначений и терминов
- •Немного о бейсиКе
- •Наивная теория множеств.
- •Декартовы произведения
- •Натуральные числа
- •Рекурсия
- •Порядок на множестве натуральных чисел
- •Делимость натуральных чисел
- •Делимость целых чисел
- •Алгоритм Евклида
- •Матричная трактовка алгоритма Евклида
- •Элементы логики
- •Высказывательные формы
- •Матричная алгебра
- •Определители
- •Обратная матрица
- •Компьютерная реализация матричной алгебры
- •Линейные преобразования плоскости
- •Комплексные числа
- •Конструкция поля комплексных чисел.
- •Сопряжение комплексных чисел
- •Тригонометрическая форма записи комплексных чисел
- •Комплексная экспонента
- •Решение квадратных уравнений.
- •Основная теорема алгебры комплексных чисел
- •Алгебраические системы
- •Операции и отношения на множестве
- •Моноиды
- •Поля и тела
- •Подсистемы алгебраических систем
- •Декартово произведение алгебраических систем
- •Фактор системы
- •Изоморфизм алгебраических систем
- •Абелевы группы
- •Группа подстановок
- •Алгебра многочленов
- •Немного комбинаторики
- •Биномиальные коэффициенты
- •Числа Фибоначчи
- •Рациональные числа
- •Дерево Штерна-Брокко
- •Алгебра высказываний
- •Дизъюнктивная совершенная нормальная форма.
- •Конъюнктивная нормальная совершенная форма
- •Многочлены Жегалкина
- •Алгебра кватернионов.
- •Литература
Высказывательные формы
Будет ли
выражение
 высказыванием? Нет, эта запись есть
высказывательная форма от одной
переменной
.
Если вместо переменной подставлять
допустимые значения, то получаем
различные высказывания, которые могут
быть как верными, так и ложными:
высказыванием? Нет, эта запись есть
высказывательная форма от одной
переменной
.
Если вместо переменной подставлять
допустимые значения, то получаем
различные высказывания, которые могут
быть как верными, так и ложными:

Внимательного рассмотрения заслуживает фраза «допустимые значения». Это какие? В данном примере область допустимых значений (ОДЗ) есть все вещественные числа. Вообще, если у нас имеется какое-либо аналитическое выражение, то под естественной ОДЗ этого выражения понимаются все объекты (это могут быть как числа, включая комплексные, так и матрицы, многочлены, функции и т.п.) при которых все операции, входящие в запись аналитического выражения, так же как и отношения, корректно определены, и мы в итоге получаем значение этого выражения. В силу каких-либо причин можно ограничить естественную ОДЗ.
Высказывательную форму можно «замкнуть» двумя существенное разными способами – применяя кванторы существования и всеобщности:


Получаются два существенно разных высказывания, а переменная при этом замыкании становится «немой», вместо нее можно подставить любой знак, при этом высказывания не изменятся. Для кванторов существования и всеобщности имеются общепринятые обозначения:

Если ОДЗ есть
конечное множество
 , то высказвание
, то высказвание
 эквивалентно конъюнкции
эквивалентно конъюнкции
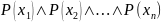 ,
а высказывание
,
а высказывание
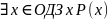 эквивалентно дизъюнкции
эквивалентно дизъюнкции
 .
.

Для
высказывательных форм от двух переменных
 требуются уже два квантора для их
замыкания. Предупреждение: порядок
использования кванторов важен. Все
возможные случаи замыкания
перечислены ниже
требуются уже два квантора для их
замыкания. Предупреждение: порядок
использования кванторов важен. Все
возможные случаи замыкания
перечислены ниже


Формально –
восемь случаев, но
 эквивалентно
эквивалентно
 и
и
 эквивалентно
эквивалентно
 .
Следовательно, остается шесть различных
способов замыкания.
.
Следовательно, остается шесть различных
способов замыкания.
ПРИМЕР.
Рассмотрим высказывательную форму
 :
:

где ОДЗ первой
переменной – положительные действительные
числа, а ОДЗ второй – натуральные числа.
Здесь
-- данная последовательность чисел, а
 -- данное число. Если мы замкнем
таким образом:
-- данное число. Если мы замкнем
таким образом:

то получим
утверждение эквивалентное
 .
Если замкнуть по другому:
.
Если замкнуть по другому:

то получим утверждение эквивалентное следующему: начиная с некоторого N последовательность постоянна и равна .
Матричная алгебра
Матричная алгебра над кольцом R (R – кольцо целых чисел, поле рациональных чисел, поле вещественных чисел) – наиболее широко используемая алгебраическая система с множеством операций как внутренних, так и внешних (сложение, умножение на элементы кольца R и умножение матрицы на матрицу, транспонирование, определитель, след, характеристический многочлен, собственные числа и т.д.). В любом языке программирования имеется возможность определять матрицы как двумерные массивы чисел. В VBA строка
Dim M(2,2) as Long (1)
задает массив-матрицу из трех строк и трех столбцов, компоненты которой – целые числа:

Если мы хотим, что бы нумерация компонент начиналась с единицы, а не с нуля, то вместо (1) надо записать
Dim M(1 to 3, 1 to 3) as Long (2)
В математическом
тексте матрицы записывают так:
 .
Тем самым задана матрица, состоящая из
m строк и n столбцов, (i,j)-ый компонент
которой, стоящий на пересечении i-ой
строки и j-ого столбца, есть
.
Тем самым задана матрица, состоящая из
m строк и n столбцов, (i,j)-ый компонент
которой, стоящий на пересечении i-ой
строки и j-ого столбца, есть
 .
.
Матрица, у
которой число строк и столбцов совпадают,
называется квадратной. Элементы
 называются главной диагональю матрицы
называются главной диагональю матрицы
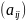 .
Единичная матрица
.
Единичная матрица
 есть квадратная матрица, у которой на
главной диагонали единицы, а остальные
все коэффициенты 0. Заметим, что две
матрицы равны, если, во-первых, совпадают
их размеры, а во-вторых, на одинаковых
местах стоят равные друг другу числа.
Матрицы
есть квадратная матрица, у которой на
главной диагонали единицы, а остальные
все коэффициенты 0. Заметим, что две
матрицы равны, если, во-первых, совпадают
их размеры, а во-вторых, на одинаковых
местах стоят равные друг другу числа.
Матрицы
 ;
;

называются
i - ой строкой и j
- ым столбцом матрицы
 .
.
Если
 еще одна матрица того же размера m×n,
то
еще одна матрица того же размера m×n,
то

Соотношение (3) определяет линейные операции над матрицами – сложение и умножение на элементы кольца R. Как видно из (3), сложение для матриц разных размеров не определено. Умножение матриц – более сложная операция. Что бы понять это определение лучше сначала обратиться к интерпретации матриц как линейных преобразований. Пусть

-- две 2×
2-матрицы. Они задают линейные преобразования
пары переменных. Пусть первая матрица
преобразует пару
 в пару
в пару
 , а вторая матрица преобразует пару
в пару
, а вторая матрица преобразует пару
в пару
 по следующему правилу
по следующему правилу

Подставим во второе соотношение вместо их линейные выражения через :
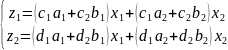
Эта процедура называется композицией преобразований. В результате мы получили линейное преобразование, задающееся матрицей

В произведении на месте (i,j) стоит скалярное произведение i-ой строки первой матрицы на j-ый столбец второй матрицы. Из интерпретации произведения матриц как последовательного выполнения преобразований немедленно вытекает ассоциативность произведения матриц (еще до формального определения произведения!), ибо композиция преобразований для любых множеств подчиняется ассоциативному закону (см. рис.)

Формальное
определение следующее. Произведение
строки
 на столбец
на столбец
 определяется как число – матрица 1х1,
равная
определяется как число – матрица 1х1,
равная
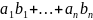 .
Произведением
.
Произведением
 матрицы
на
матрицы
на
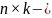 матрицу
называется
матрицу
называется
 матрица
матрица
 такая, что
такая, что
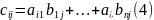
Единичная
матрица -- нейтральный элемент по
отношению к произведению матриц, то
есть
 для любой
матрицы
A.
для любой
матрицы
A.
Матрица называется нулевой, если все ее компоненты – нули. Она играет роль нейтрального элемента по отношению к сложению (A+0=0+A=A) и поглощающего элемента по отношению к умножению (0⋅ A=0).
Как уже
сказано, произведение матриц ассоциативно,
т.е. матричное равенство
 имеет место всякий раз, когда операции
умножения определены. Кроме того,
произведение дистрибутивно относительно
сложения:
имеет место всякий раз, когда операции
умножения определены. Кроме того,
произведение дистрибутивно относительно
сложения:
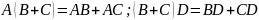
СЛЕДСТВИЕ. Совокупность n×n-матриц над кольцом R образует кольцо.
Обозначим это кольцо Mat(n×n,R). Заметим, что это кольцо не коммутативно при n>1, т.е. произведение матриц как правило зависит от порядка сомножителей. Мы уже имели дело с кольцом Mat (2× 2,ℤ ) в предыдущем параграфе.
Транспонирование
матрицы -- операция над
 -матрицей A , превращающая ее в
-матрицей A , превращающая ее в
 –матрицу
–матрицу
 , у которой
, у которой
 -ый
коэффициент равен
-ый
коэффициент равен
 -ому
коэффициенту матрицы A . Свойства
операции транспонирования следующие:
-ому
коэффициенту матрицы A . Свойства
операции транспонирования следующие:
Т1.
 ;
;
Т2.
 ;
;
Т3.
Инволютивность операции транспонирования:
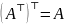 ;
;
Относительно транспонирования произведение матриц обладает следующим свойством
Т4.
 .
.
Матрица A
называется верхнетреугольной, если
ниже главной диагонали матрицы A стоят
нули. Аналогично, A - нижнетреугольная
матрица, если выше главной диагонали
матрицы A стоят нули. Матрица A
треугольная, если она либо верхнетреугольная,
либо нижнетреугольная. Треугольная
матрица с нулями на главной диагонали
называется строго треугольной. Матрица
называется диагональной, если вне
главной диагонали стоят нули. Диагональную
n×n-матрицу
обозначаем так: diag( ).
Заметим, что
).
Заметим, что



Эти соотношения показывают, что множество диагональных матриц замкнуто относительно сложения и умножения, а также содержит нейтральный элемент умножения – единичную матрицу E. В этом случае в алгебре употребляется термин «подкольцо». Подкольцом будет также совокупность верхнетреугольных (нижнетреугольных) матриц.
Алгебра матриц содержит делители нуля, например:

а также содержит нильпотентные элементы (которые в какой-либо степени обращаются в нулевой элемент):

Над строками (столбцами) матрицы можно совершать элементарные преобразования
1 тип. Прибавление к строке (столбцу) другой строки (столбца), предварительно умноженной на какой-либо элемент кольца R.
2 тип. Перестановка двух строк (столбцов).
3 тип. Умножение строки (столбца) на обратимый элемент кольца R.
Элемент u
кольца R называется
обратимым, если uv=vu=1 для некоторого
 .
В кольце целых чисел обратимых элементов
всего два -- ± 1. А в поле рациональных
чисел (как и действительных чисел, как
и в любом другом поле) все ненулевые
элементы обратимы. Это и есть причина,
по которой мы употребляем термин «поле».
Итак, поле – это коммутативное кольцо
с единицей, в котором каждый ненулевой
элемент обратим (кроме того, считаем 1≠
0, чтобы исключить случай нулевого поля).
.
В кольце целых чисел обратимых элементов
всего два -- ± 1. А в поле рациональных
чисел (как и действительных чисел, как
и в любом другом поле) все ненулевые
элементы обратимы. Это и есть причина,
по которой мы употребляем термин «поле».
Итак, поле – это коммутативное кольцо
с единицей, в котором каждый ненулевой
элемент обратим (кроме того, считаем 1≠
0, чтобы исключить случай нулевого поля).
