1. Декартовы произведения

Упорядоченная пара, или просто пара элементов 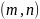это одна из фундаментальных конструкций в математики. Представлять её можно как полочку с двумя местами -- первым и вторым. Очень часто в математике неважно как на самом деле устроен тот или иной объект, а важны правила обращения с ним. Подобно этому при игре в шахматы совершенно неважно из чего сделаны фигуры и какой они в точности формы, -- важны лишь правила игры. Правило обращения с парой одно:

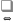( -- логический знак, заменяющий слова "тогда и только тогда, когда", "если и только если" и т.п.) Далее индуктивно можно строить упорядоченные тройки элементов, четверки элементов и т. д.:

Декартовым произведением двух множеств M и N называется множество всех пар (m,n), где m пробегает M, а элемент n пробегает N. Существование пары элементов и существование декартова произведения -- очередные аксиомы теории множеств.

ПРИМЕР. Если и , то

Общее правило подсчета элементов в декартовом произведении (правило умножения) таково:

3. Натуральные числа

Числа {1,2,3,… }, которые можно получить из единицы операцией сложения, называют натуральными и обозначают ℕ. Аксиоматическое описание натуральных чисел может быть таким (см. [М, стр. 115]): это множество ℕ на котором имеется выделенный элемент 1∈ ℕ (0-арная операция) и имеется унарная операция прибавления единицы, сопоставляющая всякому натуральному числу n натуральное число n+1, причем выполняются следующие аксиомы:

(N1) для любого натурального числа n результат n+1 не равен единице;

(N2) для любых двух натуральных чисел из равенства n+1=m+1 вытекает равенство n=m;

(N3) (метод математической индукции) пусть 𝒜 〈n〉 -- какая-либо высказывательная форма с переменной n∈ ℕ. Если высказывание 𝒜 〈1〉 верно, и для любого натурального n из 𝒜 〈n〉 вытекает 𝒜〈 n+1〉 , то утверждение 𝒜 〈n〉 верно для всех натуральных n.

Реальной интерпретацией натуральных чисел может служить какое-либо вместилище (коробка, мешок и т.д.) однородных объектов (камней, шаров, монет и т.д.). Другая, геометрическая интерпретация, -- отрезки на прямой ℓ, которые получаются в результате откладывания с помощью циркуля выбранного заранее единичного отрезка. Теоретико-множественная интерпретация, а точнее рекуррентное построение системы натуральных чисел вместе с нулем заключается в том, что мы полагаем и для каждого следующего натурального полагаем . Тогда

1. Рекурсия

От аксиом N1-N3 до знакомых всем с начальной школы операций сложения и умножения натуральных чисел, сравнения натуральных чисел между собой и свойств вида "от перемены мест слагаемых сумма не изменится" большая дистанция. Зачастую доказательство таких утверждений есть формальные проверки с многократным использованием метода математической индукции. Принципиальный момент – рекурсивные определения сложения и затем умножения натуральных чисел. В общем виде рекурсия -- это метод построения или вычисления, когда каждый следующий объект строится (вычисляется) на основе предыдущих. Абстрактно рекурсия в простейшем виде описывается отображением F:M → M и начальным значением . Далее объект вычисляется как в предположении, что уже известен.

Метод математической индукции показывает, что тогда мы получаем отображение или последовательность объектов из множества M. Сама формула называется рекуррентной и ее использование возможно лишь, если явно задано начальный объект .

Определим сложение посредством рекуррентной формулы m+(n+1):=(m+n)+1. Например,

Умножение определяется явным заданием формулы умножения на единицу: m⋅ 1:=m, а также рекуррентной формулы m⋅ (n+1):=m⋅ n+m. В частности, единица есть нейтральный элемент операции умножения. Далее доказываются фундаментальные свойства операций сложения и умножения

Ассоциативность: для любых чисел выполняются равенства

Здесь специально вместо выражения "для любых натуральных чисел" употребляется выражение "для любых чисел"; эти фундаментальные свойства верны для всех чисел.

Докажем, например, ассоциативность сложения индукцией по k. Для k=1 получаем формулу (m+n)+1=m+(n+1). Это равенство справедливо для всех натуральных чисел m и n по определению сложения. Допустим теперь, что равенство (m+n)+k=m+(n+k) для некоторого k и при любых m и n установлено и теперь нам надо проверить аналогично равенство для k+1:

Здесь во втором равенстве использовано предположение индукции, а в остальных использовано определение сложения. Ассоциативность сложения доказана в силу принципа математической индукции (см. аксиому N3). Аналогично проверяются остальные свойства сложения и умножения.

Присоединим к множеству натуральных чисел элемент ноль 0, обладающий свойствами

для любого n∈ ℕ . Получаем множество всех целых неотрицательных целых чисел, для которых перечисленные выше свойства ассоциативности, коммутативности и дистрибутивности сохраняются.