
- •Спасское Городище 2012
- •Введение
- •Список обозначений и терминов
- •Немного о бейсиКе
- •Наивная теория множеств.
- •Декартовы произведения
- •Натуральные числа
- •Рекурсия
- •Порядок на множестве натуральных чисел
- •Делимость натуральных чисел
- •Делимость целых чисел
- •Алгоритм Евклида
- •Матричная трактовка алгоритма Евклида
- •Элементы логики
- •Высказывательные формы
- •Матричная алгебра
- •Определители
- •Обратная матрица
- •Компьютерная реализация матричной алгебры
- •Линейные преобразования плоскости
- •Комплексные числа
- •Конструкция поля комплексных чисел.
- •Сопряжение комплексных чисел
- •Тригонометрическая форма записи комплексных чисел
- •Комплексная экспонента
- •Решение квадратных уравнений.
- •Основная теорема алгебры комплексных чисел
- •Алгебраические системы
- •Операции и отношения на множестве
- •Моноиды
- •Поля и тела
- •Подсистемы алгебраических систем
- •Декартово произведение алгебраических систем
- •Фактор системы
- •Изоморфизм алгебраических систем
- •Абелевы группы
- •Группа подстановок
- •Алгебра многочленов
- •Немного комбинаторики
- •Биномиальные коэффициенты
- •Числа Фибоначчи
- •Рациональные числа
- •Дерево Штерна-Брокко
- •Алгебра высказываний
- •Дизъюнктивная совершенная нормальная форма.
- •Конъюнктивная нормальная совершенная форма
- •Многочлены Жегалкина
- •Алгебра кватернионов.
- •Литература
Комплексная экспонента
Правило (2) параграфа дает нам право определить экспоненту чисто мнимого числа:

Действительно,
таким образом определенная функция
 обладает следующими свойствами:
обладает следующими свойствами:

Здесь первое
равенство есть частный случай (2), когда
 ,
второе равенство есть не что иное как
формула Муавра, а третье равенство
вытекает из периодичности гармоник.
Заметим, что никакой коллизии в обозначения
в связи с известной экспонентой
,
второе равенство есть не что иное как
формула Муавра, а третье равенство
вытекает из периодичности гармоник.
Заметим, что никакой коллизии в обозначения
в связи с известной экспонентой
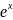 действительной переменной не возникает;
равенство аргументов
действительной переменной не возникает;
равенство аргументов
 возможно лишь если
возможно лишь если
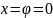 .
Но тогда определение (4) комплексной
экспоненты дает нам значение
.
Но тогда определение (4) комплексной
экспоненты дает нам значение
 ,
что совпадает с известным равенством
,
что совпадает с известным равенством
 .
.
Определение (1) позволяет записать ненулевое комплексное число в показательной форме

В таком виде легче оперировать с комплексными числами, когда речь идет об умножении, делении и возведении в степень. Например,

Решение квадратных уравнений.
Линейный
многочлен
 при
при
 всегда имеет корень
всегда имеет корень
 .
Квадратный трехчлен уже не всегда имеет
корни над полем действительных чисел.
.
Квадратный трехчлен уже не всегда имеет
корни над полем действительных чисел.
Пусть
 – квадратный трехчлен над полем
комплексных чисел (
– квадратный трехчлен над полем
комплексных чисел ( ).
Обозначим через
).
Обозначим через
 какой-либо комплексный квадратный
корень из дискриминанта
какой-либо комплексный квадратный
корень из дискриминанта
 .
Тогда
.
Тогда

суть комплексные
корни многочлена
 Действительно,
уравнение
Действительно,
уравнение
 равносильно уравнению
равносильно уравнению
 ,
откуда и следует формула (6).
,
откуда и следует формула (6).
ПРИМЕР.
Решим уравнение
 :
:

Заметим, что
как и положено по теореме Виета, сумма
корней равна
 ,
а произведение равно 13.
,
а произведение равно 13.
Основная теорема алгебры комплексных чисел
Поле называется алгебраически замкнутым, если любой многочлен над этим полем, не равный константе, имеет хотя бы один корень. Из теоремы Безу сразу следует, что над таким полем любой неконстантный многочлен разложим в произведение линейных множителей. В этом смысле алгебраически замкнутые поля устроены проще, чем не алгебраически замкнутые. Мы знаем, что над полем действительных чисел не всякий квадратный трехчлен имеет корень, тем самым поле ℝ не является алгебраически замкнутым. Оказывается ему чуть-чуть не хватает до алгебраической замкнутости. Другими словами: решив казалось бы частную задачу о уравнение , мы одновременно справились со всеми остальными полиномиальными уравнениями.
ОСНОВНАЯ ТЕОРЕМА АЛГЕБРЫ. Любой многочлен над полем ℂ, не равный константе, имеет хотя бы один комплексный корень.
СЛЕДСТВИЕ. Любой многочлен, не равный константе, над полем комплексных чисел разложим в произведение линейных множителей:

Здесь
-- старший коэффициент многочлена,
 – все различные комплексные корни
многочлена,
– все различные комплексные корни
многочлена,
 -- их кратности. Должно выполняться
равенство
-- их кратности. Должно выполняться
равенство

Доказательство следствия представляет собой несложную индукцию по степени многочлена.
Над другими
полями положение дел не столь хорошее
в смысле разложимости многочленов.
Назовем многочлен неприводимым, если
он во-первых, не константа, а, во-вторых,
не разложим в произведение многочленов
меньших степеней. Ясно, что всякий
линейный многочлен (над любым полем)
неприводим. Следствие можно переформулировать
так: неприводимыe многочлены над полем
комплексных чисел с единичным старшим
коэффициентом (по другому: унитарные)
исчерпываются многочленами вида
 (
(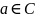 ).
).
Разложимость
квадратного трехчлена
 равносильна наличию хотя бы одного
корня. Преобразуя уравнение
равносильна наличию хотя бы одного
корня. Преобразуя уравнение
 к виду
к виду ,
заключаем, что корень квадратного
трехчлена
,
заключаем, что корень квадратного
трехчлена
 существует тогда и только тогда, когда
дискриминант
существует тогда и только тогда, когда
дискриминант
 есть квадрат какого-либо элемента поля
K (здесь предполагаем, что 2≠ 0 в поле K).
Отсюда получаем
есть квадрат какого-либо элемента поля
K (здесь предполагаем, что 2≠ 0 в поле K).
Отсюда получаем
ПРЕДЛОЖЕНИЕ.
Квадратный трехчлен
над полем K, в котором 2≠ 0, неприводим
тогда и только тогда, когда он не имеет
корней в поле K. Это равносильно тому,
что дискриминант
 не является квадратом никакого элемента
поля K. В частности, над полем действительных
чисел квадратный трехчлен
неприводим, если и только, если
не является квадратом никакого элемента
поля K. В частности, над полем действительных
чисел квадратный трехчлен
неприводим, если и только, если
 .
.
Итак над полем действительных чисел существуют по крайней мере два вида неприводимых многочленов: -- линейные и квадратичные и отрицательным дискриминантом. Оказывается, что эти два случая исчерпывают множество неприводимых многочленов над ℝ.
ТЕОРЕМА. Любой многочлен над полем действительных чисел разложим в произведение линейных множителей и квадратичных множителей с отрицательными дискриминантами:

Здесь
 -- все различные действительные корни
многочлена
-- все различные действительные корни
многочлена
 ,
-- их кратности, все дискриминанты
,
-- их кратности, все дискриминанты
 меньше нуля, и квадратные трехчлены
меньше нуля, и квадратные трехчлены
 все различны.
все различны.
Вначале докажем лемму
ЛЕММА.
Если
 и
и
 для какого-либо
для какого-либо
 ,
то сопряженное число
,
то сопряженное число
 также является корнем многочлена
также является корнем многочлена
 .
.
Доказательство.
Пусть ,
,
 и
– комплексный корень многочлена
.
Тогда
и
– комплексный корень многочлена
.
Тогда
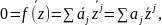
где мы
использовали свойства сопряжения.
Следовательно,
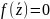 .
Тем самым
-- корень многочлена
.
Тем самым
-- корень многочлена
 .
□
.
□
Доказательство
теоремы. Достаточно доказать, что любой
неприводимый многочлен над полем
действительных чисел либо линейный,
либо квадратичный с отрицательным
дискриминантом. Пусть
 -- неприводимый многочлен с единичным
старшим коэффициентом. В случае
-- неприводимый многочлен с единичным
старшим коэффициентом. В случае
 сразу получаем
сразу получаем
 для некоторого действительного
.
Предположим, что
для некоторого действительного
.
Предположим, что
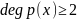 .
Обозначим через
.
Обозначим через
 какой-либо комплексный корень этого
многочлена, существующий по основной
теореме алгебры комплексных чисел. Так
как
какой-либо комплексный корень этого
многочлена, существующий по основной
теореме алгебры комплексных чисел. Так
как
 неприводим, то
неприводим, то
 (см.
теорему Безу). Тогда по лемме,
будет еще одним корнем многочлена
,
отличным от
.
(см.
теорему Безу). Тогда по лемме,
будет еще одним корнем многочлена
,
отличным от
.
Многочлен
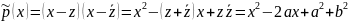 имеет
действительные коэффициенты. Кроме
того,
имеет
действительные коэффициенты. Кроме
того,
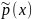 делит
согласно теореме Безу. Так как
неприводим и имеет единичный старший
коэффициент, то получаем равенство
делит
согласно теореме Безу. Так как
неприводим и имеет единичный старший
коэффициент, то получаем равенство
 .
Дискриминант этого многочлена отрицателен,
так как иначе он имел бы вещественные
корни.□
.
Дискриминант этого многочлена отрицателен,
так как иначе он имел бы вещественные
корни.□
ПРИМЕРЫ.
А. Разложим
многочлен
 на неприводимые множители. Среди
делителей константного члена 6 ищем
корни многочлена. Убеждаемся, что 1 и 2
– корни. Тем самым многочлен делится
на
на неприводимые множители. Среди
делителей константного члена 6 ищем
корни многочлена. Убеждаемся, что 1 и 2
– корни. Тем самым многочлен делится
на
 .
Поделив, находим
.
Поделив, находим

--
окончательное разложение над полем
 ,
ибо дискриминант квадратного трехчлена
,
ибо дискриминант квадратного трехчлена
 отрицателен и, следовательно, он над
полем действительных чисел далее не
разложим. Разложение того же многочлена
над полем комплексных чисел получим,
если найдем комплексные корни квадратного
трехчлена
.
Они суть
отрицателен и, следовательно, он над
полем действительных чисел далее не
разложим. Разложение того же многочлена
над полем комплексных чисел получим,
если найдем комплексные корни квадратного
трехчлена
.
Они суть
 .
Тогда
.
Тогда

--
разложение данного многочлена над

Б.
Разложим
 над полями действительных и комплексных
чисел. Так как действительных корней
этот многочлен не имеет, то он разложим
на два квадратных трехчлена с отрицательными
дискриминантами
над полями действительных и комплексных
чисел. Так как действительных корней
этот многочлен не имеет, то он разложим
на два квадратных трехчлена с отрицательными
дискриминантами

Так
как при замене
на
 многочлен не меняется, то при такой
замене квадратный трехчлен
многочлен не меняется, то при такой
замене квадратный трехчлен
 должен переходить в
должен переходить в
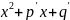 и наоборот. Отсюда
и наоборот. Отсюда
 и
и
 .
Приравнивая коэффициенты при
.
Приравнивая коэффициенты при
 получаем
получаем
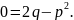 В частности,
В частности,
 .
Тогда из соотношения
.
Тогда из соотношения
 (получается подстановкой
(получается подстановкой
 извлекаем
извлекаем
 ,
и окончательно,
,
и окончательно,
 .
Итак,
.
Итак,

-- разложение над полем действительных чисел.
Для
того, чтобы разложить данный многочлен
над комплексными числами, решим уравнение
 или
или
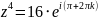 .
Ясно, что
.
Ясно, что
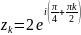 будут корнями. Все различные корни мы
получим при
будут корнями. Все различные корни мы
получим при
 .
Следовательно,
.
Следовательно,


Тогда

-- разложение над комплексными числами. Легко вычислить

и мы получаем другое решение задачи о разложении многочлена над полем действительных чисел.
