Таблица 1.4

Фракции пыли

Размеры частиц на границах фракций, мкм	Фракции, % от общей массы частиц	Размеры частиц на границах фракций, мкм	Фракции, % от общей массы частиц
меньше 1,6 1,6-2,5 2,5-4 4-6,3	2,08 4,61 9,32 18,56	6,3-10 10-16 16-25 25-40	25,2 19,74 12,97 7,52

Таблица 1.5

Фракции пыли с частицами больше или меньше заданного размера

Размер час- тиц, мкм	Общая масса частиц, %		Размер час- тиц, мкм	Общая масса частиц, %
	мельче (D)	крупнее (R)		мельче (D)	крупнее (R)
Min	0	100	10	54,17	45,83
1,6	2,08	97,92	16	72,91	27,09
2,5	5,69	94,31	25	87,48	12,52
4,0	14,01	85,99	max	100	0
6,3	31,57	68,43

Интегральные кривые для частиц с логарифмически нормальным распределением удобно строить в вероятностно-логарифмической системе координат, где они приобретают вид прямых линий (рис. 1.8). Для построения такой системы координат по оси абсцисс в логарифмическом масштабе откладывают значения d_ч, а по оси координат значения D(d_ч) или R(d_ч). Относительные длины отрезков х, соответствующих различным значениям D(d_ч) или R(d_ч), которые для построения в вероятностно-логарифми­ческой системе координат следует откладывать в выбранном масштабе от начала оси абсцисс приведены ниже.

Поскольку в вероятностно-логарифмической системе координат ось абсцисс начинается от точки на оси ординат, соответствующей значению 50%, значения х для D(d_ч) или R(d_ч) больше 50% откладываются вверх от начала оси абсцисс, а меньше 50% — вниз.

Рис. 1.5. Гистограмма распределения по фракциям

Рис. 1.6. Дифференциальная кривая распределения

Кривая «+»

Кривая «–»

Рис. 1.7. Интегральное распределение в линейной системе координат

Построив по результатам дисперсного анализа интегральную функцию распределения частиц по размерам в вероятностно-логариф­мической системе координат, можно (если получившийся график имеет вид прямой линии, свидетельствующий о логарифмически нормальном характере изучаемого распределения) выразить это распределение в виде параметров d_m и lg _ч.

Рис. 1.8. Интегральное распределение в вероятностно-логарифмической системе координат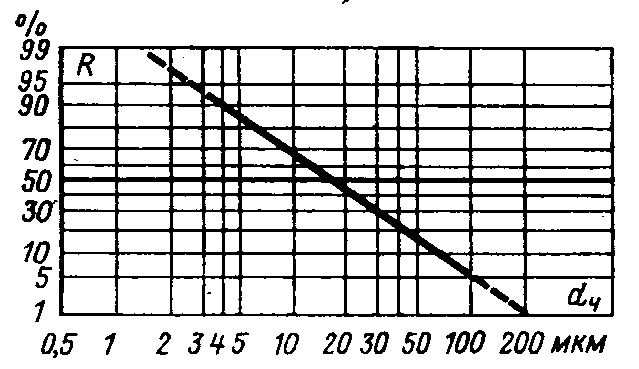

Значению d_m отвечает точка пересечения построенного графика с осью абсцисс, а lg _ч находится из соотношения, которое является свойством интеграла вероятности: lg _ч = lg d_15,9 – lg d_m = lg d_m – lg d_84,1, если строится график функции R(d_ч), или lg _ч = lg d_84,1 – lg d_m = lg d_m – lg d_15,9. Здесь lg d_15,9 и lg d_84,1 — абсциссы точек, ординаты которых имеют значения 84,1 и 15,9.

Дисперсный состав пыли, образующейся при некоторых технологических процессах представлен в табл. 1.7.

ГОСТ 12.2.043-80 подразделяет все пыли на 5 групп в зависимости от дисперсности:

I — очень крупнодисперсная пыль;

II — крупнодисперсная пыль (например, песок для строительных растворов);

III — среднедисперсная пыль (например, цемент);

IV — мелкодисперсная пыль (например, кварц молотый пылевидный);

V — очень мелкодисперсная пыль.

Несмотря на то, что ГОСТ 12.2.043-80 не действует на территории РФ, данная классификация используется при выборе пылеулавливающего оборудования.

Для определения дисперсности пыли используют следующие методы:

— ситовый анализ — разделение частиц на фракции путем пос­ледовательного просеивания навески пыли через лабораторные сита с отверстиями различных размеров. Применяют для исследования пыли, в которой масса частиц мельче 100 мкм составляет не более 10%;

— седиментометрия — разделение навески пыли на фракции путем ее осаждения в жидкой среде (жидкостная седиментация);