
4.3. Технологія побудови двовимірних графіків в MatLab
Система MATLAB володіє широкими можливостями для графічного представлення результатів обчислень і візуалізації даних.
Виведення відображення функції
![]()
у вигляді графіка складається з наступних етапів:
задання вектора значень аргумента x;
обчислення вектора y значень функції y(x);
виклик команди plot для побудови графіка.
Команди для задання вектора x і обчислення функції краще завершувати крапкою з комою, що дозволяє уникнути виведення в командне вікно їх значень:
>> x=0:0.01:1;
>> y=exp(-x).*sin(10*x);
>>plot(x,y)
Для побудови графіка функції в робочому середовищі MATLAB® повинні бути визначені два вектори однакових розмірів, наприклад x та y. Вектор x містить значення аргументів, а y – значення функції цих аргументів.
Команда plot з’єднує точки з координатами (x(i), y(i)) прямими лініями, автоматично масштабуючи осі для найкращого візуального розміщення графіка по осях.
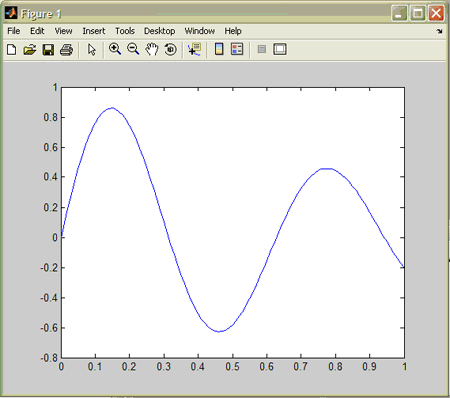
Рис. 2. Графік функції
Якщо ж відображення графічного результату в системі за замовчуванням користувачу не підходить, можна параметри візуалізації задати індивідуально для кожного графіка, або налаштувати їх вже після відображення результату. Використовуючи кнопку DockFigure (справа в стрічці меню вікна) можна вмонтувати графічне вікно в робоче середовище.
Порівняння декількох функцій зручно виконувати, якщо їх графіки відобразити в одній системі координат.
Для побудови графіків функцій і потрібно набрати наступну послідовність команд:
>>x = -1:0.005:-0.3;
>> f = sin(x.^-2);
>> g = sin(1.2*x.^-2);
>>plot(x, f, x, g)
Також з допомогою команди plot можна задати стиль та колір ліній, наприклад:
>>plot(x, t, ‘k-‘, x, g, ‘k:’)
Аргументи ‘k-‘ і ‘k:’ задають стиль і колір першої та другої ліній. Тут k означає чорний колір, а дефіс або двокрапка – неперервну або пунктирну лінію.
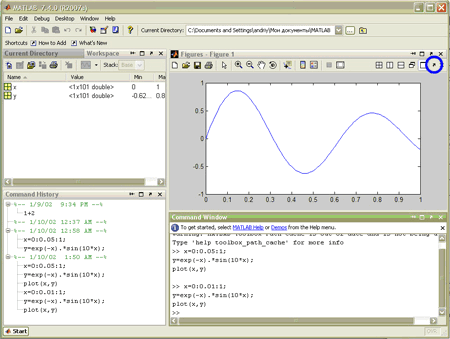
Рис. 3. Розміщення вікна з графіком у середовищі MATLAB
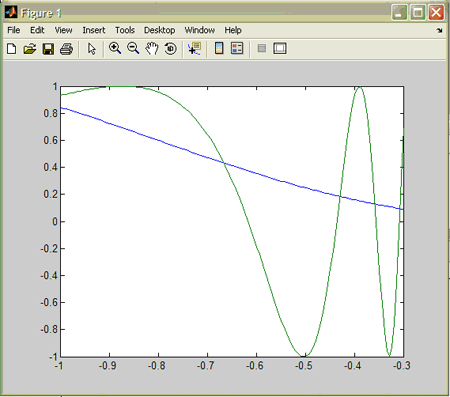
Рис. 4. Два графіка на одних осях
4.4. Технологія побудови тривимірних графіків
Настільки ж просто забезпечуєтьсяпобудоваграфіківскладнихповерхонь. Треба тільки знати, якою командою реалізується той чиіншийграфік. Наприклад, для побудовиграфікаповерхні і їїпроекції у вигляді контурного графіка на площинупідповерхнеюдоситьвикористовуватинаступнікоманди.
» [X.Y]=meshgrid(-5:0.1:5);
» Z=X.*sin(X+Y);
» meshc(X.Y,Z)

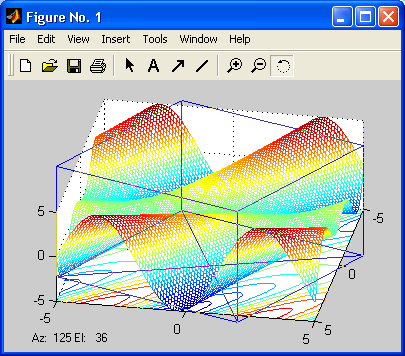
Рис. 5. Вікно з графіками поверхні і її проекції на площину під фігурою
Раніше довелося б вбити багато днів на складання і налагодження потрібної для побудови такого графіка програми. В MATLAB же можна в лічені секунди змінити задану поверхню функцію Z (X, Y) і тут же отримати новий графік поверхні з забарвленням, в даному випадку заданої вектором Z, і з її проекцією на площину XY. На рис. 1 показано також відкрите меню Help (Допомога) вікна тривимірної графіки.
Ми обмежимося цими прикладами побудови графіків як досить простими і типовими. З них випливає важливий висновок - для вирішення тієї чи іншої приватної завдання треба знати відповідні команди і функції. У цьому вам допоможуть як дана книга, так і довідкова система MATLAB.
Крім того, можуть використовуватися такі спеціальні тривимірні структури. Одна з них - структура:
GRID (a.. B, c.. D, listlist) - завдання поверхні над ділянкою координатної площини [a, b] ([c, d] за даними заданим списковій змінної listlist: = [[zll, ... zln], [z21, ... z2n ],...[ zml ... zmn]] з розмірністю nxm.
Ще один тип тривимірної графічної структури це:
MESH (listlist) - завдання тривимірної поверхні за даними облікової змінної listlist, що містить повні координати всіх точок поверхні (завдання останньої можливо при нерівномірній сітці).
4.5. Розв’язання диференційного рівняння


де
А1=0.3, А0=0.5, К=0.4
Рішення за допомогою MATLAB
S=dsolve('D2y-0.3*Dy+0.5*y-exp(-0.4*x)=0','y(0)=0','Dy(0)=9','x')
S =7570/7449*exp(3/20*x)*sin(1/20*191^(1/2)*x)*191^(1/2)-50/39*exp(3/20*x)*cos(1/20*191^(1/2)*x)+50/39*exp(-2/5*x)
4.6. Розв’язання систем лінійних рівнянь

Рішення за допомогою MATLAB
A=[2 -1 1 2; 1 2 3 -1; 2 -3 2 -2; 3 3 -2 4];
b=[5;3;2;5]
x=inv(A)*b
x =
1
0
1
1
4.7.Обчислення похідних за варіантом

Рішення за допомогою MATLAB
syms s
y =Bil[s*(s^3+(s^2)*Bil(s/2))]
diff(y,s)
ans =
Bil(s*(s^3+s^2*Bil(1/2*s)))*(s^3+s^2*Bil(1/2*s)+
s*(3*s^2+2*s*Bil(1/2*s)+1/2*s^2*Bil(1/2*s)))
4.8.Обчислення невизначених та визначених інтегралів


Рішення за допомогою MATLAB
syms s
int(Bil(s*(s^3+(s^2)*Bil(s/2))))
ans = -d^2*Bil(d)+2*Bil(d)+2*Bil(d)*d+2*Bil(1/2*d)+Bil(1/2*d)*d-2/9*Bil(3/2*d)-1/3*Bil(3/2*d)*d


Рішення за допомогою MATLAB
z1 = int(Bil(s*(s^3+(s^2)*Bil(s/2)))+d,d,0,9)
vpa(z1,5)
ans = 104.36
4.9. Проектування моделі автопілоту літака по каналу крена
Коефіцієнти моделі автопілоту літака по каналу крена
Таблиця 1.
№ |
К1 |
К2 |
К3 |
К4 |
К5 |
К6 |
К7 |
9 |
0.1 |
8 |
8 |
11.6 |
1.2 |
1.4 |
1 |

Рис. 6. Система управління моделі автопілоту літака по каналу крена
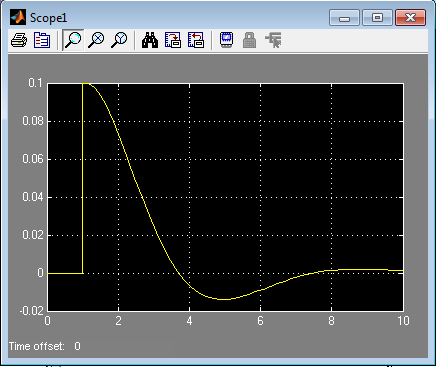
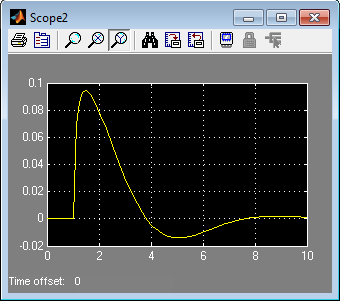

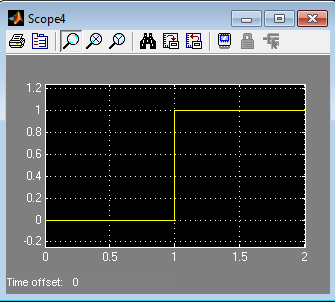
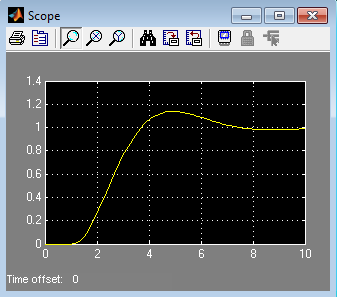
Рис. 7. Графіки роботи моделі автопілоту
