3.3.3Уравнения движения потока жидкости

Уравнение постоянство расхода и неразрывности потока.

Рассмотрим установившееся движение жидкости в русле переменного сечения (Рисунок 2.2.3.1).

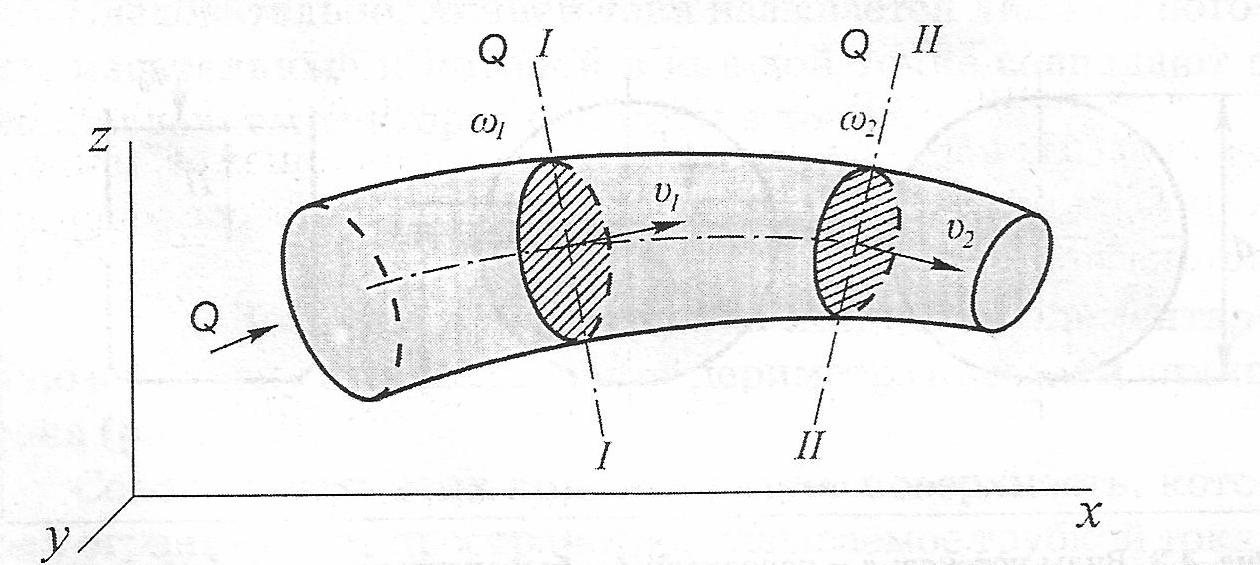
Рисунок 2.2.3.1 - Установившееся движение жидкости в русле переменного сечения

Жидкость несжимаема и в ней невозможно образования пустот. Это условие неразрывности потока жидкости.

Выберем два произвольных сечения I-I и II-II, перпендикулярных к оси потока, и рассмотрим заключенный между ними отсек жидкости. Через сечение I-I за время t в этот отсек войдет масса жидкости m₁, а через сечение II-II за это время выйдет масса жидкости m₂.

Так как жидкость несжимаема, а стенки русла жесткие, то при отсутствии разрыва в потоке и согласно закону сохранения вещества можно записать равенство масс m в сечениях I-I и II-II:

m

(2.2.3.1)

₁ = m₂ = const,

известно, масса определяется как

(2.2.3.2)

где , - плотность жидкости в сечениях I-I и II-II, , - расход жидкости в сечениях I-I и II-II.

Т

(2.2.3.3)

аким образом выражение можно записать в следующем виде:

.

Т

(2.2.3.4)

ак как жидкость несжимаема, то , и выражение можно записать так:

(вдоль потока)

Это уравнение называется уравнением постоянства расхода. Из него следует, что при установившемся движении несжимаемой жидкости расход ее в любом сечении потока постоянен.

И

(2.2.3.5)

з уравнения постоянства потока (вдоль потока) получается другое важное уравнение движения жидкости. Так как расход записывается в виде , то уравнения постоянства расхода можно записать в следующем виде:

(вдоль потока)

которое и называется уравнением неразрывности потока жидкости. Из уравнения неразрывности потока следует, что при установившемся движении несжимаемой жидкости произведение средней скорости на площадь живого сечения потока является величиной постоянной. Из уравнения также можно получить:

(2.2.3.6)

,

т.е. в установившемся потоке жидкости средние скорости движения обратно пропорциональны площадям соответствующих живых сечений.

3.3.4Трубка Пито. Измерение скорости потока

Гидродинамическая трубка Пито предназначена для определения местных скоростей (осредненных во времени) в точках живого сечения безнапорного потока жидкости (Рисунок 2.2.4.1).

Трубка Пито, впервые примененная в 1732 г. французским инженером-гидротехником А. Пито, представляет собой изогнутую под прямым углом трубку, устанавливаемую открытым концом отогнутой части навстречу потоку так, чтобы центр отверстия трубки совпал с точкой потока, в которой определяется скорость движения жидкости. Второй, верхний, конец трубки выводится из потока наружу.

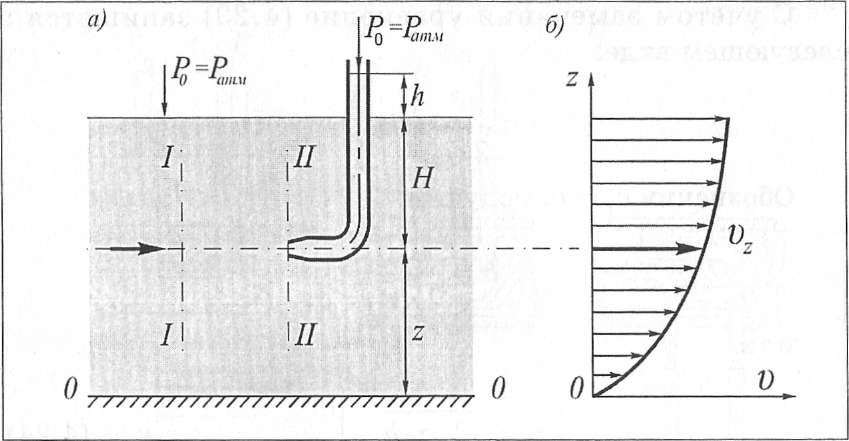
Рисунок 2.2.4.1 - Гидродинамическая трубка Пито (а) и эпюра распределения скоростей (б).

Когда трубку Пито устанавливают навстречу потоку жидкости, в трубку попадают частицы жидкости и уровень воды в трубке увеличивается на высоту h.

Поднятие жидкости на дополнительную высоту в трубке Пито объясняется тем, что движущиеся частицы жидкости, набегая на входной конец трубки со скоростью υ, осуществляют дополнительное давление на неподвижную жидкость в скоростной трубке, для уравновешивания которого жидкость в ней должна подняться на дополнительную высоту, уравновешивающую скоростной напор υ²/(2g)

Зная величину дополнительного подъема жидкости h в трубке Пито, можно из выражения

h

(2.2.4.1)

= υ²/(2g)

н

(2.2.4.2)

айти величину скорости движения потока жидкости:

где h - высота подъема жидкости в трубке Пито по сравнению с уровнем жидкости в пьезометре, g - ускорение свободного падения.

Д

(2.2.4.3)

ействительная скорость в рассматриваемой точке потока будет несколько отличаться от скорости, определяемой выражением (2.2.4.2), за счет того, что жидкость, обтекая носик трубки, вызывает некоторые местные нарушения структуры потока. Поэтому действительная скорость определяется скорректированным выражением

где коэффициент ξ определяется опытным путем при та­рировании трубки.

Перемещая носик трубки по вертикали в сечении потока, определяют скорость жидкости в различных точках взятой вертикали и получают так называемую эпюру распределения скорости по данной вертикали живого сечения потока (Рисунок 2.2.4.1).