3.2.2Основное уравнение гидростатики

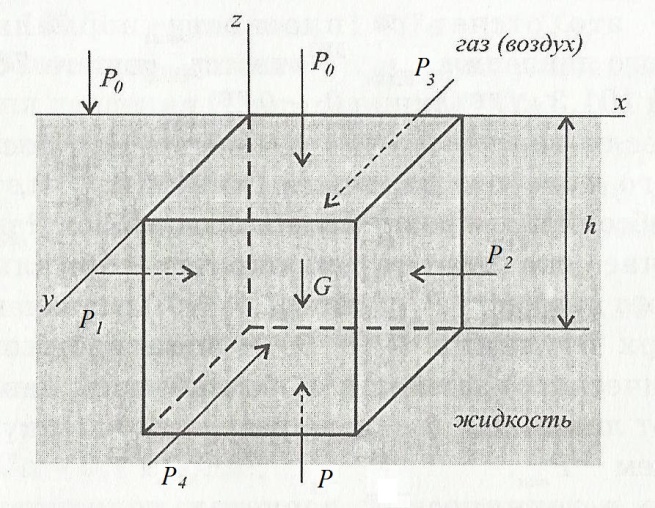
Рисунок 2.1.2.1 - Схема к выводу основного уравнения гидродинамики

Уравнение, определяющее гидростатическое давление в любой точке покоящейся жидкости, является основным уравнением гидростатики.

Рассмотрим выделенный параллелепипед покоящейся жидкости.

У рассматриваемого параллелепипеда имеются четыре боковые грани, на которые со стороны жидкости действуют силы Р₁, Р₂, Р₃ и Р_4, и две горизонтальные грани.

Силы Р₁, Р₂, Р₃ и Р₄ попарно равны между собой (Р₁=Р₂ и Р₃=Р₄), т.е. уравновешиваются между собой и в дальнейшем не учитываются.

На верхнюю горизонтальную грань, совпадающую со свободной поверхностью жидкости, действует поверхностная сила Р₀. В нашем случае, она равняется атмосферному давлению р_а.

На нижнюю горизонтальную грань, расположенную на глубине h, действует сверху вниз массовая сила, т.е. сила тяжести всего параллелепипеда G.

Тот факт, что жидкий параллелепипед не проваливается вниз под действием сил Р₀ и G, свидетельствует о существовании в нижней грани силы P, которая и уравновешивает силы, направленные вниз. Силу P называют силой гидростатического давления и она направлена cверху вниз.

В

(2.1.2.1)

итоге, согласно уравнениям равновесия можно записать

,

где Р – сила гидростатического давления, действующая снизу вверх на нижнюю грань параллелепипеда, расположенную на глубине h от свободной поверхности, Р₀ – поверхностная сила, действующая сверху вниз на верхнюю грань параллелепипеда, G – массовая сила, т.е. сила тяжести всего параллелепипеда жидкости, действующая сверху вниз.

В свою очередь силу G можно представить как

(2.1.2.2)

,

где m – масса жидкости параллелепипеда, g - ускорение свободного падения, – плотность жидкости, V – объем параллелепипеда жидкости, - удельный вес жидкости, , S – площадь горизонтальной грани параллелепипеда, h – глубина расположения нижней грани от свободной поверхности.

О

(2.1.2.3)

бъем параллелепипеда равен

,

П

(2.1.2.4)

одставим величину G в выражение, получим

,

Отнеся каждую составляющую выражения к площади S

(2.1.2.5)

,

И приняв обозначения

(2.1.2.6)

и ,

П

(2.1.2.7)

олучим в окончательном виде, основное уравнение гидростатики

,

где Р_абс – абсолютное гидростатическое давление точек на нижней грани параллелепипеда, Р₀ – поверхностное давление на свободную поверхность, – избыточное или манометрическое гидростатическое давление на нижнюю грань параллелепипеда, расположенную на глубине h от свободной поверхности.

Из уравнения (2.1.2.7) следует, что абсолютное гидростатическое давление Р_абс в любой точке жидкости, находящейся в абсолютном покое, равно сумме поверхностного давления Р₀ и давления вызванного силой тяжести столба жидкости h, расположенного над рассматриваемой точкой.

Основное уравнение гидростатики можно рассмотреть и с другой стороны.

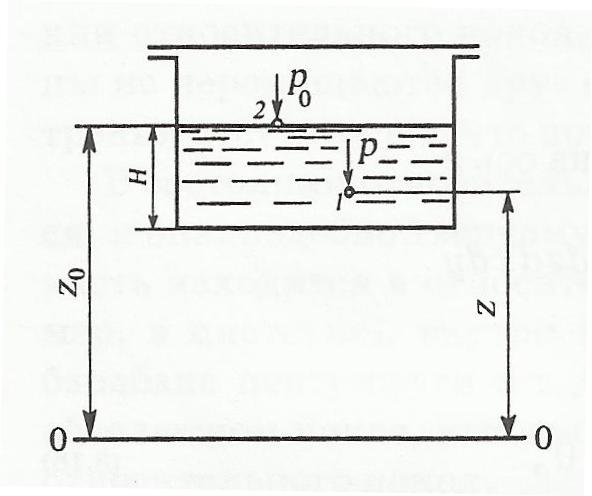
Рисунок 2.1.2.2 - Схема к выводу основного уравнения

Пусть у нас имеется сосуд с покоящейся жидкостью, с высотой столба жидкости H. Выделим в этой жидкости две точки, которые расположены на высотах z и z₀.

Из выше сказанного понимаем, что давление в покоящейся жидкости изменяется только по вертикали, оставаясь одинаковым во всех точках любой горизонтальной плоскости, т.к. изменения давлений вдоль осей х и у равны нулю.

Таким образом:

(2.1.2.8)

А для двух произвольных горизонтальных плоскостей уравнение (2.1.2.8) выражают в виде:

(2.1.2.9)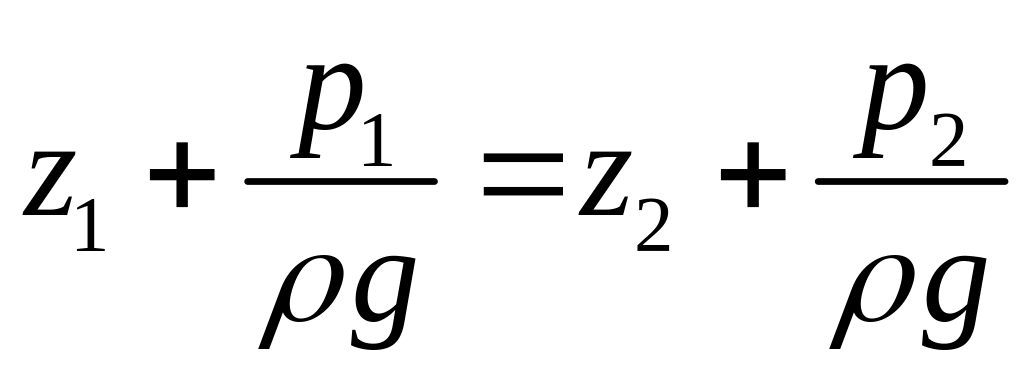

,

где z₁ и z₂ – высоты расположения двух точек внутри покоящейся однородной капельной жидкости, р₁ и р₂ – гидростатическое давление в этих точках.

Уравнение (2.1.2.8) или (2.1.2.9) является основным уравнением гидростатики.

Оно выражает зависимость давление данной точки покоящейся жидкости от рода жидкости (ее плотности) и расстояния точки по вертикали от свободной поверхности.

Член z в уравнении гидростатики (2.1.2.8), представляющий собой высоту расположения данной точки над произвольно выбранной плоскостью сравнения, называется нивелирной или геометрической высотой. Величину называют высотой давления, или пьезометрической высотой.

Согласно основному уравнению гидростатики, для каждой точки покоящейся жидкости сумма нивелирной и пьезометрической высот есть величина постоянная.

Члены основного уравнения гидростатики имеют определенный энергетический смысл. Так, выражение члена до сокращения характеризует удельную энергию, т.е. энергию, приходящуюся на единицу веса жидкости, и называют пьезометрическим напором. Энергетический смысл получает и нивелирная высота, если ее выражение умножить и затем разделить на единицу веса жидкости.

Таким образом, нивелирная высота z, называемая также геометрическим (высотным) напором, характеризует удельную потенциальную энергию положения данной точки над выбранной плоскостью сравнения, а пьезометрический напор – удельную потенциальную энергию состояния в этой точке. Сумма указанных энергий, называемая полным гидростатическим напором, равна общей потенциальной энергии, приходящейся на единицу веса жидкости. Следовательно, основное уравнение гидростатики представляет собой частный случай закона сохранения энергии: удельная потенциальная энергия во всех точках покоящейся жидкости есть величина постоянная.