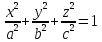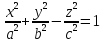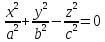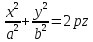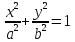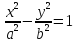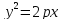Решение системы линейных уравнений ()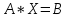

Методом Крамера: вычислить 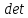исходной матрицы и 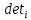матриц, заменив i-ый столбец на матрицу . 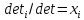Если 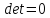, то решений .

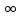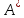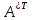С помощью обратной матрицы: вычисляем матрицу из миноров , затем и 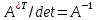(проверка: 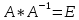). 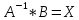( 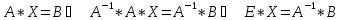или )

Методом Гаусса: привести матрицу 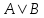к ступенчатому виду. Если 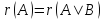, то по теореме Кронекера-Капелли система совместна. Если 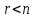, то первые 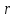переменных – базисные, остальные – свободные.

Векторы

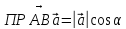
Скалярное произведение векторов – число, равное

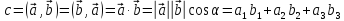
Векторы 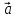и 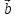ортогональны (перпендикулярны)

Векторное произведение векторов – вектор, длина которого равна 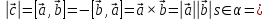определителю матрицы

Смешанное произведение векторов – число, равное определителю матрицы

По модулю равно объему парал., построенного на них.

Векторы 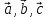компланарны (лежат в 1-й плоскости)

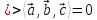
Прямая

Каноническое

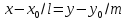
Через 2 точки

Общее уравнение

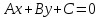
Параметрические у.

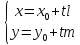
У. в отрезках

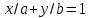
У. с угл. коэф.

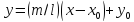
Нормальное

Эллипс

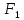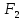Это множество точек плоскости, сумма расстояний от каждой из которых до 2-х заданных точек и есть величина постоянная, большая, чем расстояние между фокусами.

Каноническое уравнение

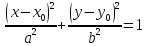
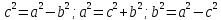
– большая полуось; 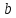– малая полуось; 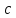– фокальное расстояние.

Вершины:

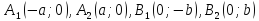
Фокусы: 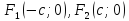или

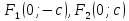
Эксцентриситет 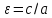характеризует вытянутость.

Директрисы 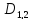: 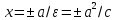– это такая прямая, что для любой точки отношение расстояний до фокуса и до прямой равно эксцентриситету.

Гипербола

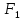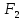Это множество точек плоскости, модуль разности от каждой из которых до 2-х заданных точек и есть величина постоянная, меньшая, чем расстояние между фокусами.

Каноническое уравнение

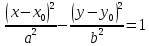
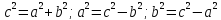
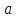– большая полуось; 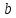– малая полуось; 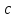– фокальное расстояние.

Вершины: – действительные; – мнимые.

Фокусы: 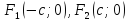или 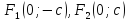; фокусы лежат на действительной оси

Эксцентриситет 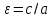характеризует вытянутость.

Директрисы : 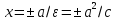– это такая прямая, что для любой точки отношение расстояний до фокуса и до прямой равно эксцентриситету.

Парабола

Каноническое уравнение

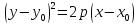
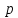– фокальный параметр, равен расстоянию от фокуса до директрисы

Вершина:

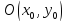
Фокус:

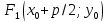
Эксцентриситет 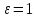характеризует вытянутость.

Директриса :

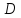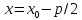
Название	Канонич. уравн.	Вершины	Фокусы	Эксц.	Директрисы
Эллипс	x^2/a^2+y^2/b^2=1	A1 (-a;0), A2 (a;0), B1 (0;-b), B2 (0;b)	F1 (-с;0), F2 (с;0) или F1 (0;-с), F2 (0;с)	ε=c/a	x=±a/ε=±a^2/c
Гипербола	x^2/a^2-y^2/b^2=1	A1 (-a;0), A2 (a;0); B1 (0;-b), B2 (0;b)	F1 (-с;0), F2 (с;0) или F1 (0;-с), F2 (0;с)	ε=c/a	x=±a/ε=±a^2/c
Парабола	y^2=2px^2	O (x_0,y_0 )	F1 (x_0+p/2;y_0 )	ε=1	x=x_0-p/2

Поверхности вращения

Эллипсоид (объёмный овал)
Гиперболоид однополостной
Гиперболоид двуполостной
Конус
Параболоид эллиптический (чаша)
Параболоид параболический (чипс)
Цилиндр эллиптический
Цилиндр гиперболический
Цилиндр параболический