1.2. Типы ошибок измерений
Несовпадение результатов опытов может быть вызвано тремя причинами.
1. Если в ходе эксперимента были допущены грубые отклонения от граничных условий его проведения (неисправность оборудования, невнимательность исполнителя, ошибка в дозировке компонентов смеси и т.п.), то ошибки, возникающие вследствие этого, относят к типу грубых ошибок. При обнаружении грубой ошибки результат следует отбросить, а эксперимент повторить. Внешним признаком грубой ошибки результата измерения является резкое отклонение его числового значения от результатов остальных измерений. Если причина появления ошибки известна, результат немедленно исключается из анализа, а опыт повторяется при тех же граничных условиях. Если причина появления таких результатов не может быть установлена, то следует известными математическими приемами (см. п.1.5 данного пособия) произвести выбраковку результата.
2. Если в контрольной серии опытов при известном значении Y величины Yi смещены относительно Y в одну сторону, то ошибку измерений относят к типу систематических. Причиной появления систематических ошибок чаще всего являются неправильная регулировка прибора, изменение условий проведения эксперимента, если заранее известно влияние этих изменений на конечный результат (температура образца при измерении его удлинения и т.п.). Как только систематические ошибки обнаружены и рассчитаны, их легко учесть в конечном результате, вводя в расчет его значения соответствующие поправки с учетом их знака.
3. Ошибки измерения, остающиеся после учета всех вышеназванных, называются случайными. Случайные ошибки вызываются большим количеством факторов, эффекты действия которых незначительны. Таким образом, случайную ошибку можно рассматривать как суммарный эффект действия неконтролируемых исследователем факторов. Исходя из этого, можно полагать, что результаты параллельных опытов образуют набор случайных величин, анализ точности и достоверности которых осуществляется методами математический статистики и теории вероятности.
1.3. Распределение случайных ошибок измерения
Случайные ошибки измерения характеризуются определенным законом их распределения.
Под распределением случайной величины понимается совокупность всех возможных ее значений и соответствующих им вероятностей.
Соответствие значений случайной величины вероятности ее появления формулируется в виде закона распределения случайной величины. Существование такого закона можно обнаружить, измеряя много раз в неизменных условиях некоторую величину и подсчитывая число результатов измерений, которые попадают в любой выделенный интервал значений измеряемой случайной величины. В качестве закона распределения случайных ошибок чаще всего принимается нормальный закон распределения (закон Гаусса), который при достаточно большом числе повторов проявляется в том, что:
абсолютные отклонения одинаковой величины, но разного знака встречаются одинаково часто;
большие по модулю абсолютные отклонения встречаются реже, чем меньшие, то есть вероятность появления погрешности уменьшается с увеличением модуля этой погрешности.
Функция плотности нормального распределения случайной величины задается двумя параметрами: истинным значением Y и его средним квардатическим отклонением сигма . Квадрат среднего квадратического отклонения получил название дисперсии случайной величины и является количественной характеристикой разброса результатов Yi вокруг истинного значения Y. На рис. 1 изображены кривые плотности нормального распределения при различных значениях дисперсии.
Нормальный закон распределения случайных ошибок хорошо согласуется с опытом и отражает известное свойство симметрии случайных ошибок (ошибки разных знаков встречаются одинаково часто) и свойство их концентрации (малые по абсолютной величине случайные ошибки встречаются чаще, чем большие). Статистика показывает, что уже вероятность выхода ошибки за пределы трехсигмовой величины ничтожно мала (составляет величину 0,0027) и считается, что случайные ошибки измерения ограничены по абсолютной величине значением 3, хотя математическая модель допускает любые их значения.
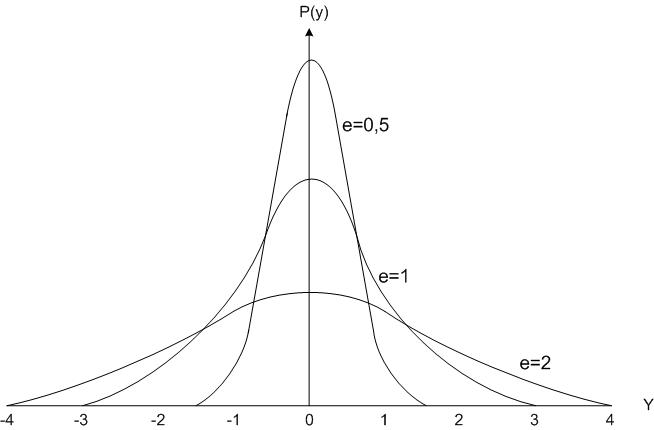
Рис. 1. Кривые плотности нормального распределения