3.2. Графические решения двумерных задач

Рассмотрение графического метода решения задач, обладающего высокой степенью наглядности, позволяет выявить некоторые общие свойства задач линейного программирования, которые указывают на пути их общего решения.

Упражнение №8. Минимизировать функцию Z=–3Х₁–4Х₂ при ограничениях X₁≥10, X₂≥5, Х₁+Х₂≤20,–Х₁+4Х₂≤20.

Графическое решение задачи на рис. 8.

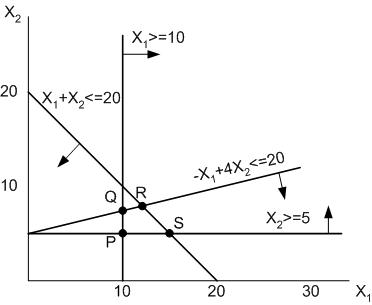
Рис. 8. Область допустимых значений для упражнения № 8

Допустимой областью является четырехугольник PQRS. Функция Z убывает в направлении вектора (3,4). Минимальное значение функции Z= –68 достигается в точке R(12,8). Обратим внимание на то обстоятельство, что и как в упражнении № 7 экстремум достигается в вершине допустимой области.

В некоторых случаях задача может иметь более одного решения.

Упражнение №9. Минимизировать функцию Z= 6Х₁–2Х₂ при ограничениях X₁≥0, X₂≥0, 2Х₁+4Х₂≤9, 3Х₁+Х₂≤6.

Допустимой областью является четырехугольник OABC. Функция Z убывает в направлении вектора (2,6). С учетом этого обстоятельства любая точка на отрезке BC является оптимальным решением.

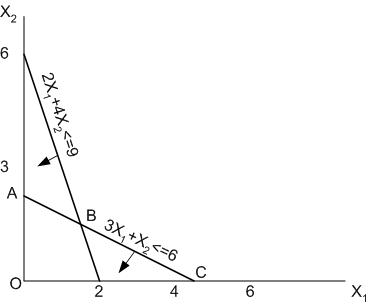
Рис. 9. Область допустимых значений для упражнения № 9

В некоторых случаях оптимальное решение не имеет ограничения.

Упражнение № 10. Максимизировать функцию Z=Х₁+Х₂ при ограничениях X₁≥0, X₂≥0, Х₁-Х₂≥1, Х₂≤2.

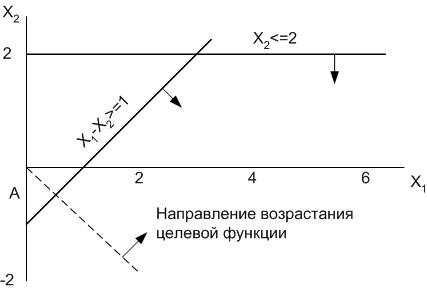
Рис. 10. Область допустимых значений для упражнения № 10

Допустимая область не ограничена в направлении возрастания функции Z. Решение также не ограничено.

В некоторых случаях задача может и не иметь решений, поскольку допустимой области не существует.

Упражнение №11. Минимизировать функцию Z=2Х₁+3Х₂ при ограничениях X₁≥0, X₂≥0, Х₁+Х₂≥10, 3Х₁+5Х₂≤15.

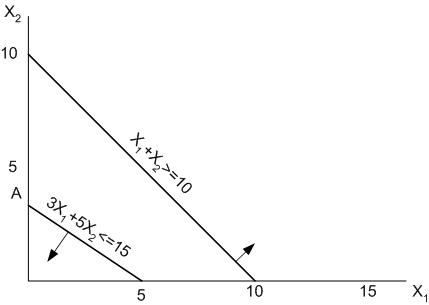
Рис. 11. Графическое решение задачи для упражнения № 11

Из рассмотренных примеров выявляются некоторые характерные особенности оптимальных решений.

1. Допустимая область решения задачи – выпуклый многоугольник, даже в случае, когда решение не имеет ограничения.

2. Оптимальное решение задачи всегда достигается в вершине (вершинах) допустимой области.

Все вышесказанное может иметь обобщения. Сначала покажем, что задачи линейного программирования могут быть приведены к стандартной форме.

3.3. Стандартная форма задач линейного программирования

Все возможные формы задач линейного программирования могут быть сведены к стандартной форме, в которой целевая функция должна быть линейной, а все ограничения должны быть заданы в виде равенств с неотрицательными переменными.

Правила перевода к стандартной форме следующие.

1. Максимизация целевой функции

Z=c₁X₁+c₂X₂+...+c_nX_n

равносильна минимизации функции

Zⁱ= –c₁X₁–c₂X₂–...–c_nX_n.

2. Ограничения в виде неравенств, например X₁+X₂-X₃≤6, могут быть приведены к стандартной форме X₁+X₂-X₃+X₄=6, где новая переменная X₄ неотрицательна.

3) Если некоторая переменная X_k может принимать любые значения, а требуется, чтобы она была неотрицательна, то ее можно привести в виду X_k=X_k*–X_k**, где X_k*≥0, X_k**≥0. Таким образом, приведение задачи к стандартной форме может потребовать дополнительных неотрицательных переменных.

Исходя из вышесказанного, упражнение № 7, который мы рассмотрели ранее, может быть приведен к следующему виду: минимизировать функцию Z= 2X₁–4X₂ при ограничениях

3X₁+4X₂+X₃ =1700,

2X₁+5X₂ +X₄=1600

X_i>=0, i=1,2,...,4.

Задача состоит из двух уравнений с четырьмя неизвестными. Любое неотрицательное решение при этих ограничениях является допустимым. Интересными решениями таких уравнений являются такие, когда два неизвестных приравниваются нулю. Если такое решение единственное, оно называется БАЗИСНЫМ. Если оно также и допустимое – это БАЗИСНОЕ ДОПУСТИМОЕ РЕШЕНИЕ. Для общей задачи линейного программирования с N переменными и M уравнениями (N>M), базисные решения ограничений могут быть получены, если приравнять нулю (N–M) переменных. Эти переменные получили название небазисных переменнных. Остальные переменные образуют БАЗИС.

В рассмотренной задаче возможны 6 комбинаций небазисных переменных (табл. 11).

Таблица 11

№	Значения переменных				Точки многоугольника
	X1	X2	X3	X4
1	0	0	1700	1600	O
2	0	425	0	–525
3	0	320	420	0	A
4	566,7	0	0	466,7	C
5	800	0	–700	0
6	300	200	0	0	B

Только четыре комбинации нулевых небазисных переменных являются допустимыми и именно они соответствуют вершина допустимой области на рис. 7.