Страничная модель памяти

Особенностью этого преобразования является то, что процессор в этом случае оперирует с блоками физической памяти равной длины (4 Кбайт) - страницами. Страницы не имеют непосредственного отношения к логической структуре программы. Страничное преобразование действует только в защищенном режиме и включается установкой в 1 бита PG в регистре CR0.

В страничном преобразовании участвуют два типа структур: каталоги таблиц (Page Directory) и таблицы страниц (Page Table). Эти структуры состоят из 1024 32-битных элементов. Элементы содержат старшие 20 бит физического адреса адресуемых объектов. Элементы таблицы страниц (Page Table Entry - PTE) адресуют страницы, а элементы каталога таблиц (Page Directory Entry - PDE) адресуют таблицы страниц. Старшие 20 бит физического адреса каталога таблиц хранятся в регистре CR3 (Page Directory Base Register - PDBR) (это единственный регистр процессора, который содержит физический адрес памяти). Все структуры выровнены по границе страницы.

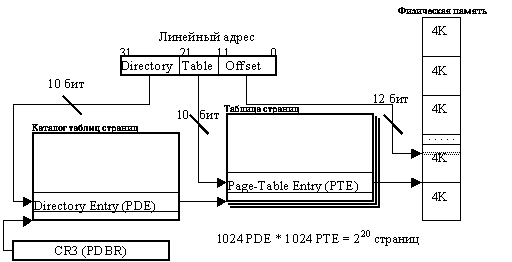
В процессе страничной трансляции адресов полученный линейный адрес разбивается на три части. Старшие десять бит (Directory) линейного адреса являются индексом элемента из каталога таблиц. По этому элементу определяется физический адрес таблицы страниц. Биты 21-12 (Table) линейного адреса выбирают элемент из этой таблицы страниц. Выбранный элемент определяет физический адрес страницы. Младшие 12 бит (Offset) линейного адреса определяют смещение от начала страницы.

Страницы начинаются на границах 4 Кбайт областей памяти, поэтому младшие 12 бит адреса страницы всегда равны нулю. В каталоге таблиц элементы хранят физические адреса таблиц страниц. В таблице страниц элементы хранят физические адреса самих страниц.

Лекция 5. Типы данных. Форматы команд. Форматы и типы данных

В связи с необходимостью решения различных прикладных задач на ЭВМ общего назначения, уже начиная с машин второго поколения отчетливо наметилась тенденция к созданию универсального набора команд. Такой универсальный набор охватывал как разнообразные форматы данных, т.е. количество занимаемых объектом битов, так и различные типы данных, т.е. внутреннюю структуру формата данных.

Рассмотрим наиболее используемые в рамках универсальных ЭВМ форматы и типы данных.

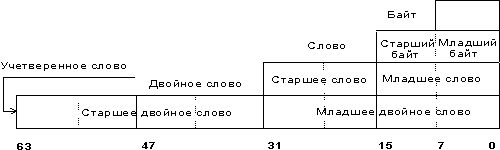
Рис.5.1. Форматы данных

Форматы данных

• байт — восемь последовательно расположенных битов, пронумерованных от 0 до 7, при этом бит 0 является самым младшим значащим битом;

• слово — последовательность из двух байт, имеющих последовательные адреса. Размер слова — 16 бит; биты в слове нумеруются от 0 до 15. Байт, содержащий нулевой бит, называется младшим байтом, а байт, содержащий 15-й бит - старшим байтом. Микропроцессоры Intel имеют важную особенность — младший байт всегда хранится по меньшему адресу. Адресом слова считается адрес его младшего байта. Адрес старшего байта может быть использован для доступа к старшей половине слова.

• двойное слово — последовательность из четырех байт (32 бита), расположенных по последовательным адресам. Нумерация этих бит производится от 0 до 31. Слово, содержащее нулевой бит, называется младшим словом, а слово, содержащее 31-й бит, - старшим словом. Младшее слово хранится по меньшему адресу. Адресом двойного слова считается адрес его младшего слова. Адрес старшего слова может быть использован для доступа к старшей половине двойного слова.

• учетверенное слово — последовательность из восьми байт (64 бита), расположенных по последовательным адресам. Нумерация бит производится от 0 до 63. Двойное слово, содержащее нулевой бит, называется младшим двойным словом, а двойное слово, содержащее 63-й бит, — старшим двойным словом. Младшее двойное слово хранится по меньшему адресу. Адресом учетверенного слова считается адрес его младшего двойного слова. Адрес старшего двойного слова может быть использован для доступа к старшей половине учетверенного слова.

Типы данных

Микропроцессор может обрабатывать числа следующих типов:

• Целый тип без знака;

• Целый тип со знаком;

• Двоично - десятичный тип;

• Типы данных с плавающей точкой.

Рассмотрим сначала целые числа без знака и со знаком.

Целый тип без знака - двоичное значение без знака, размером 8, 16 или 32 бита. Числовой диапазон для этого типа следующий:

байт - от 0 до 255;

слово - от 0 до 65 535;

двойное слово - от 0 до 2³²-1.

Отметим некоторую особенность представления чисел в ПК: числа размером в слово и двойное слово хранятся в памяти в «перевернутом виде». Так у числа размером в слово старшие (левые) 8 битов размещаются во втором байте слова, а младшие (правые) 8 битов – в первом байте. Зачем это сделано? Первые модели ПК были 8-разрядными, в них за раз можно было считать из памяти один байт. Поскольку в этих условиях многозначное число нельзя считать из памяти сразу целиком, то в первую очередь считывался байт с младшими цифрами числа, а для этого надо, чтобы такой байт хранился в памяти первым. По этой причине в первых ПК и появилось «перевернутое» представление чисел. В последующих моделях ради сохранения преемственности, ради того, чтобы ранее составленные программы могли без изменений выполняться на новых ПК, сохранили это «перевернутое» представление чисел.

Целый тип со знаком - двоичное представление со знаком размером 8, 16 или 32 бита. Знак в этом двоичном числе содержится в 7, 15 или 31 бите соответственно.

7 6 5 4 3 2 1 0

Модуль числа

Знаковый разряд

Ноль в этих битах в операндах соответствует положительному числу, а единица - отрицательному. Числовые диапазоны для этого типа данных следующие:

8-разрядное целое - от -128 до +127;

16-разрядное целое - от -32 768 до +32 767;

32-разрядное целое - от -2 ³¹  до +2 ³¹ -1.

В вычислительной технике принято записывать отрицательные числа в так называемом дополнительном коде, который образуется из прямого путем замены всех двоичных нулей единицами и наоборот (обратный код) и прибавления к полученному числу единицы. Это справедливо как для байтовых (8-битовых) чисел, так и для чисел размером в слово или в двойное слово.

доп(x)=

Такой способ образования отрицательных чисел удобен тем, что позволяет выполнять над ними арифметические операции по общим правилам с получением правильного результата. Так, сложение чисел +5 и -5 дает 0; в результате вычитания 3 из 5 получается 2; вычитание -3 из -5 дает -2 и т.д.

Среди команд процессора, выполняющих ту или иную обработку чисел, можно выделить команды, безразличные к знаку числа (например, inc, add, test), команды, предназначенные для обработки чисел без знака (mul, div, ja, jb и др.), а также команды, специально рассчитанные на обработку чисел со знаком (imul, idiv, jg, jl и т.д.). Особенности использования этих команд будут описаны в следующей главе.

Двоично-десятичные числа – специальный вид представления числовой информации, в основу которого положен принцип кодирования каждой десятичной цифры числа группой разрядов из 4-х бит. При этом каждый байт числа содержит 1 или 2 десятичные цифры в так называемом двоично-десятичном коде (BCD – Binary Coded Decimal), Микропроцессор может хранить такие числа в 2-х форматах:

• упакованный формат – в байте 2 десятичные цифры, при этом старшая цифра занимает старшие 4 бита, диапазон представления чисел в одном байте составляет 00-99;

Пример. Десятичное число 8754031 0 8 7 5 4 0 3 1 представимо в упакованном формате BCD-числа следующим образом: 0000 1000 0111 0101 0100 0000 0011 0001

• неупакованный формат - в байте 1 цифра в 4 младших битах. Старшие биты все имеют нулевое значение и называются зоной.

Пример. Десятичное число 5801 0 5 0 8 0 0 0 1 представимо в неупакованном формате BCD-числа следующим образом: 0000 0101 0000 1000 0000 0000 0000 0001

Представление чисел в двоичном коде с плавающей точкой.

Существует два общих формата для хранения значений с плавающей точкой, которые были разработаны для процессоров Intel, а затем были стандартизированы организацией IEEE. Существует стандарт IEEE 754 для представления чисел с одинарной точностью (float) и с двойной точностью (double). Для записи числа в формате с плавающей точкой одинарной точности требуется тридцатидвухбитовое слово. Для записи чисел с двойной точностью требуется шестидесятичетырёхбитовое слово. Чаще всего числа хранятся в нескольких соседних ячейках памяти процессора. Форматы числа в формате с плавающей точкой одинарной точности и числа в формате с плавающей точкой удвоенной точности приведены на рисунке

Для одинарной точности 1 бит используется для знака, 8 бит для экспоненты и 23 бита для мантиссы.

Для двойной точности 1 бит используется для знака, 11 бит для экспоненты и 52 бита для мантиссы.

На рисунке буквой S обозначен знак числа, 0 - это положительное число, 1 - отрицательное число.

Е (e) – экспонента. Экспоненты коротких реальных значений хранятся как 8-разрядные целые числа без знака, с уклоном 127. Например, число 1.101 x 2⁵. Экспонента (5) добавляется к 127 и сумма (132) в бинарном виде = 10100010. Двоичная экспонента - без знака, поэтому она не может быть отрицательной. Максимальное значение экспоненты - 128, которое при добавлении 127 дает 255 - максимальное значение для 8 бит. Примерный диапазон - 1.0 x 2^-127 to 1.0 x 2⁺¹²⁸.

m-мантисса. В десятичной мантиссе после запятой могут присутствовать цифры 1:9, а в двоичной - только 1. Поэтому для хранения единицы после двоичной запятой не выделяется отдельный бит в числе с плавающей точкой. Единица подразумевается, как и двоичная запятая. Кроме того, в формате чисел с плавающей точкой принято, что мантисса всегда больше 1. То есть диапазон значений мантиссы лежит в диапазоне от 1 до 2.

Рассмотрим несколько примеров:

1) Определить число с плавающей точкой, лежащее в четырёх соседних байтах: 11000001 01001000 00000000 00000000

- Знаковый бит, равный 1 показывает, что число отрицательное.

- Экспонента 10000010 в десятичном виде соответствует числу 130. Вычтя число 127 из 130, получим число 3.

- Теперь запишем мантиссу: 1,100 1000 0000 0000 0000 0000

- И, наконец, определим десятичное число: 1100,1b = 12,5d

2) Определить число с плавающей точкой, лежащее в четырёх соседних байтах:

11000011 00110100 00000000 00000000

- Знаковый бит, равный 1 показывает, что число отрицательное.

- Экспонента 10000110 в десятичном виде соответствует числу 134. Вычтя число 127 из 134, получим число 7.

- Теперь запишем мантиссу: 1,011 0100 0000 0000 0000 0000

- И, наконец, определим десятичное число: 10110100b=180d