Вопросы для самопроверки

1. С помощью каких показателей исследуется степень корреляционной связи между атрибутивными признаками?

2. Как располагают числовой материал для исследования связи между атрибутивными признаками?

Задача. Исследуйте степень корреляционной связи между атрибутивными признаками по данным, приведенным в табл. 2.28.

Таблица 2.28

	Число рабочих
	в литейных цехах	на конвейере
Больные Здоровые	241 56 375 189		297 564
	616 245

6. Прогнозирование взаимосвязей экономических

Явлений на основе факторных регрессионных моделей

После построения регрессионной модели, оценки существенности ее параметров

и проверки адекватности модель используется для предсказания значений зависимой переменной при определенных значениях переменных .

Естественно полагать, что действительные значения зависимой переменной не будут совпадать с расчетным (прогнозными), так как сама линия регрессии описывает взаимосвязь лишь в среднем, а отдельные наблюдения рассеяны вокруг нее. Таким образом, первым и наиболее очевидным фактором, во многом определяющим надежность получаемых по уравнению регрессии прогности­ческих оценок, является рассеяние наблюдений вокруг линии регрессии. В качестве меры рассеяния используется дисперсия. Оценка дисперсии отклонений от регрессии определяется по формуле

Важное значение при нахождении прогноза имеет определение доверительных интервалов для значений т.е. границ, в пределах которых с заданной доверительной вероятностью будет находиться значение . Вследствие того, что оценивание параметров осуществляется по выборочным данным, оценки параметров регрессии содержат некоторую погрешность.

Построим вначале доверительный интервал для парной регрессии. Дисперсию переменной определим как сумму дисперсий слагаемых уравнения . Тогда

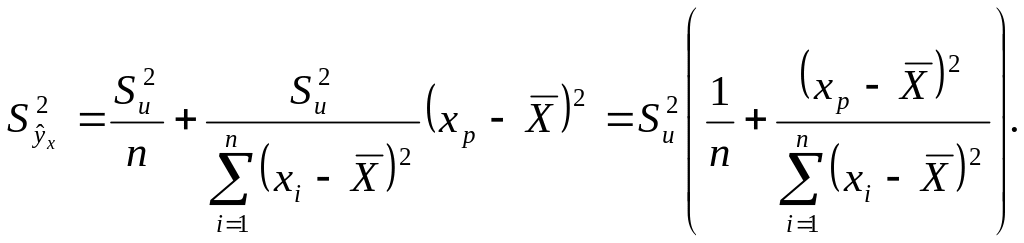
Вычислив дисперсию показателя определим доверительный интервал для расчетного значения :

где - квантиль распределения Стьюдента для уровня значимости и степеней свободы.

Построенные таким образом доверительные интервалы определяют местоположение

линии регрессии, т.е. средних значений но не отдельных возможных значений переменной Y, которые отклоняются от средней.

Если же мы хотим определить доверительные интервалы для отдельных значений зависимой переменной, то при определении дисперсии необходимо учитывать еще рассеяние вокруг линии регрессии, т.е. нужно включить величину в суммарную дисперсию:

.

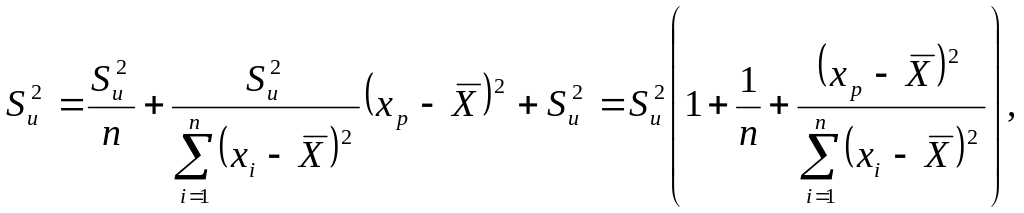
Тогда доверительные интервалы для прогнозов индивидуальных значений Y будут равны

.

В параграфе 2.3 было построено уравнение регрессии . Определим среднее значение выпуска валовой продукции на одного среднегодового работника сельского хозяйства при фондовооруженности, равной 20,541. Получим .

Для построения доверительного интервала прогноза вычислим дисперсию:

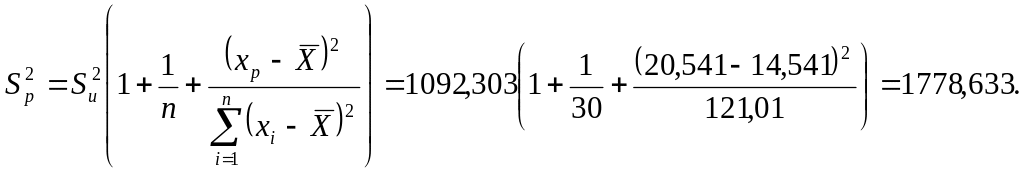
Таким образом, доверительный интервал прогнозируемого выпуска валовой продукции для фондовооруженности, равной 20,541, будет иметь вид

или    (10 036,802;  17 329,198).

Пусть прогнозируемое значение Y определяется по уравнению регрессии с оцененными параметрами

.

Так как - несмещенные оценки некоторых неизвестных параметров соответствующей взаимосвязи, то - одно из возможных значений прогнозируемой величины при заданных значениях X. Поскольку - случайная величина, то и оценка также случайная и имеет дисперсию. Определим ее значение:

.

Использовав теорему о дисперсии суммы зависимых величин (см. [2, § 4.3]), получим

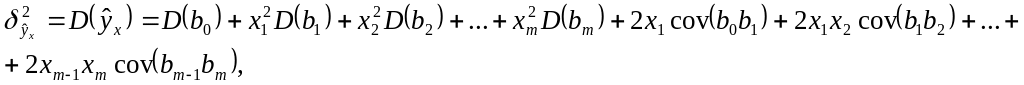или в матричной записи:

где - вектор заданных значений независимых переменных. Так как , то

.

Поскольку значение нам неизвестно, то, подставив ее оценку получим

.

Таким образом, “истинное” среднее значение Y лежит в пределах

.

Доверительный интервал для при более точно можно трактовать следующим образом: в 95 % случаев оценивания параметров регрессии одного уравнения (по выборкам с тем же числом данных) доверительные интервалы будут содержать истинные средние значения Y для заданных . Под прогностическим значением Y можно понимать его математическое ожидание, т.е. XB. Однако более естественно в прогностическое значение Y включить отклонение, т.е. рассматривать XB + U. В этом случае к дисперсии Y необходимо добавить и дисперсию U, т.е. Таким образом, получим

.

Соответственно доверительные интервалы для индивидуальной прогностической

оценки Y равны

.

Пример 2.7. Валовая продукция на одного среднегодового работника сельского хозяйства Y (ден. ед.) по 15 колхозам зависит от двух переменных и , где - энерговооруженность (л.с.); - фондовооруженность одного работника, занятого в сельскохозяйственном производстве (тыс. ден. ед./чел.). Взаимосвязь характеризуется данными, указанными в табл. 2.29.

Т а б л и ц а 2.29

№ п/п	Y
1 10 532 32,339 14,482 2 11 079 28,310 14,397 3 8 698 29,600 12,280 4 7 032 26,095 10,397 5 12 805 33,332 14,888 6 8 854 28,136 12,012 7 10 702 31,287 12,819 8 9 089 29,773 12,626 9 9 332 26,876 13,444 10 11 982 30,187 15,043 11 13 037 36,886 17,627 12 9 643 33,707 14,470 13 8 358 31,712 13,096 14 11 208 28,109 14,449 15 11 471 33,722 16,526
153 822 460,061 208,556

Предположим, что между рассматриваемыми величинами теоретиче­ски существует линейная зависимость:

.

Для оценки параметров воспользуемся методом наименьших квадратов, применив который, будем иметь соответствующую систему нормальных уравнений (2.14), решив

которую, получим

.

Таким образом, .

Естественно, что оценки параметров найденного уравнения регрессии будут отклоняться от истинных значений. Дисперсия уравнения регрессии зависит от дисперсии оценки каждого параметра уравнения. Для того чтобы измерить дисперсии оценок параметров, необходимо найти дисперсию ошибок:

,

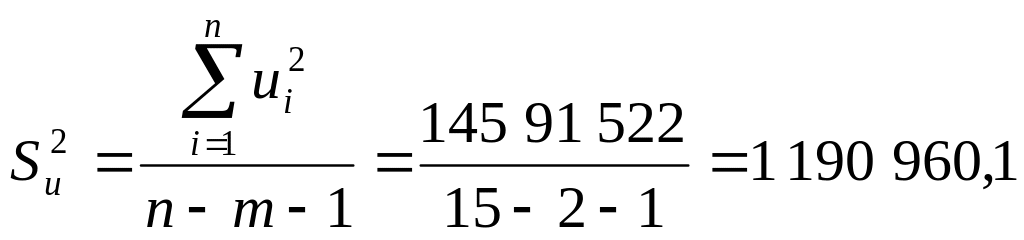а также матрицу :

,

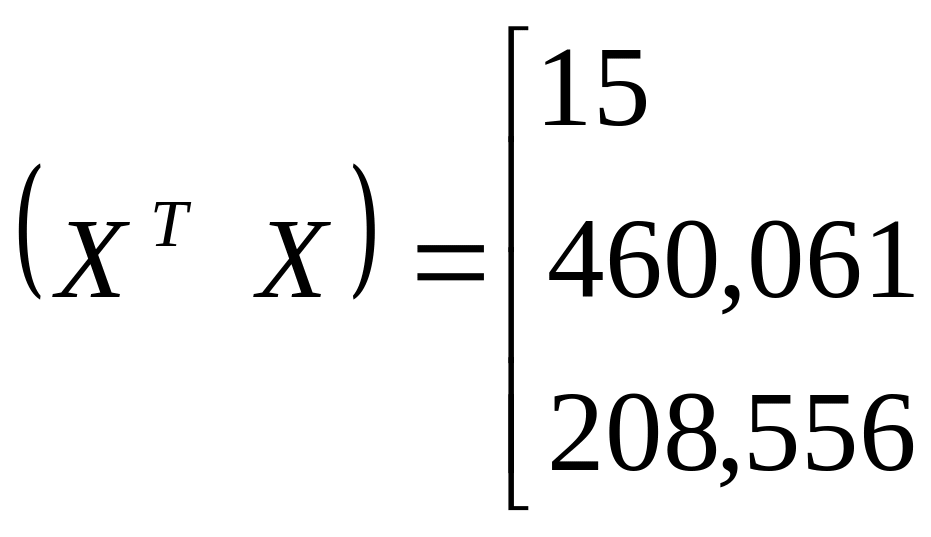
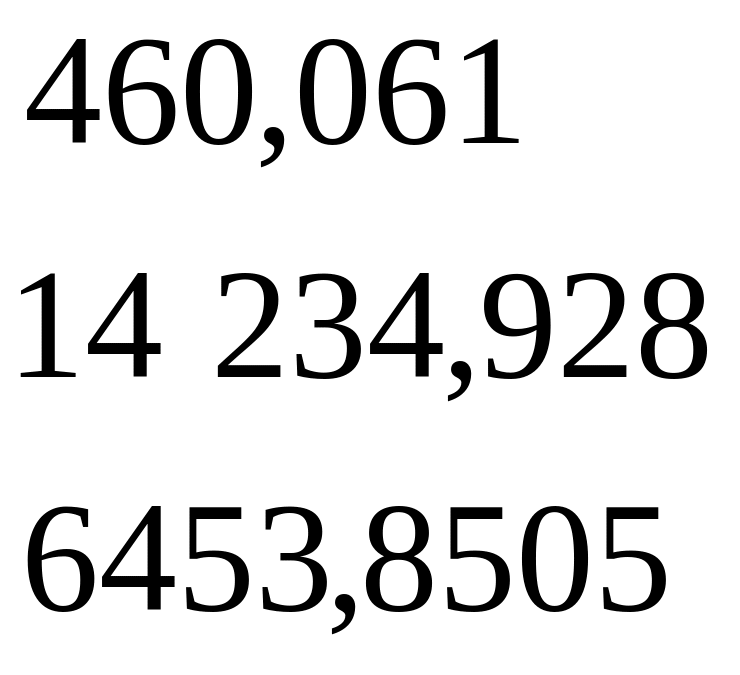
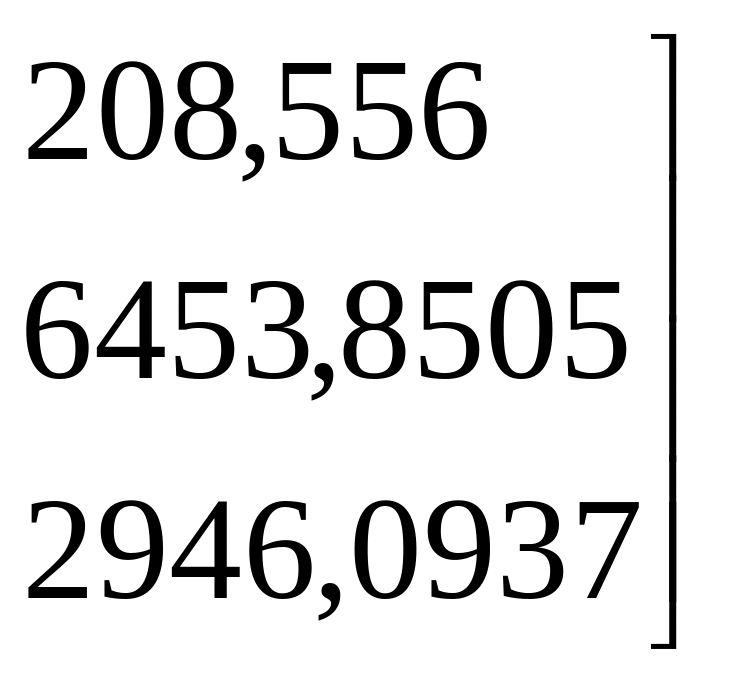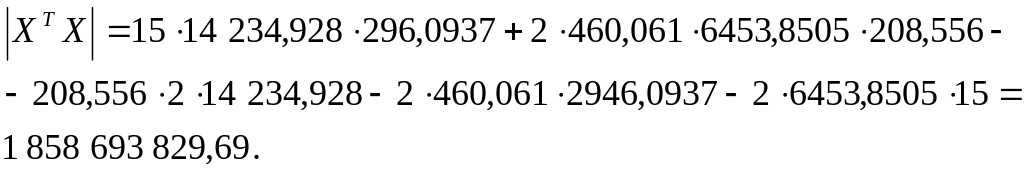
Обратную матрицу найдем как произведение обратного значения определителя на матрицу алгебраических дополнений:

.

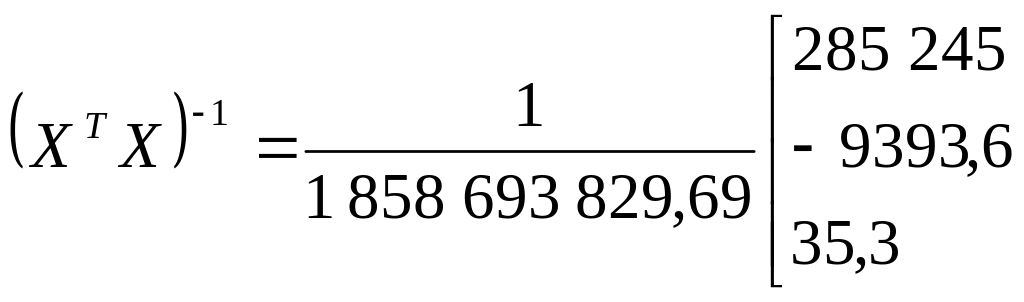
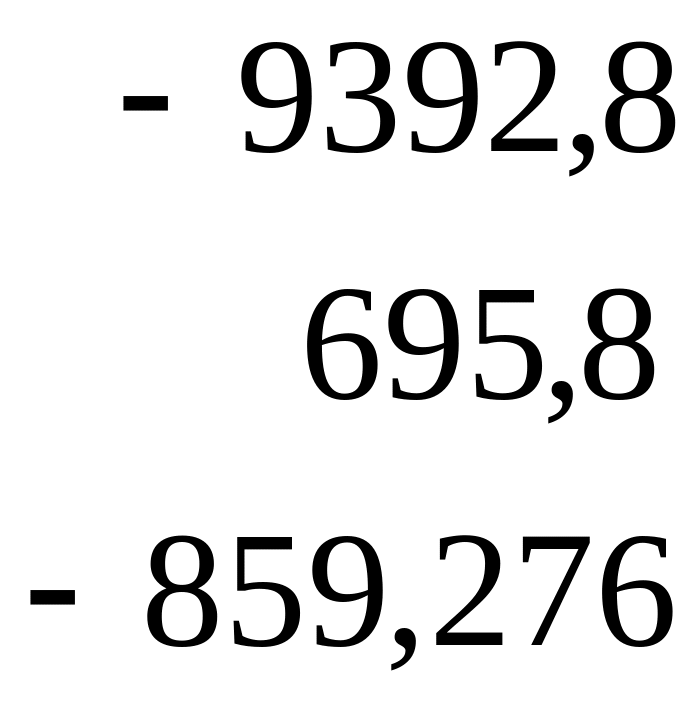
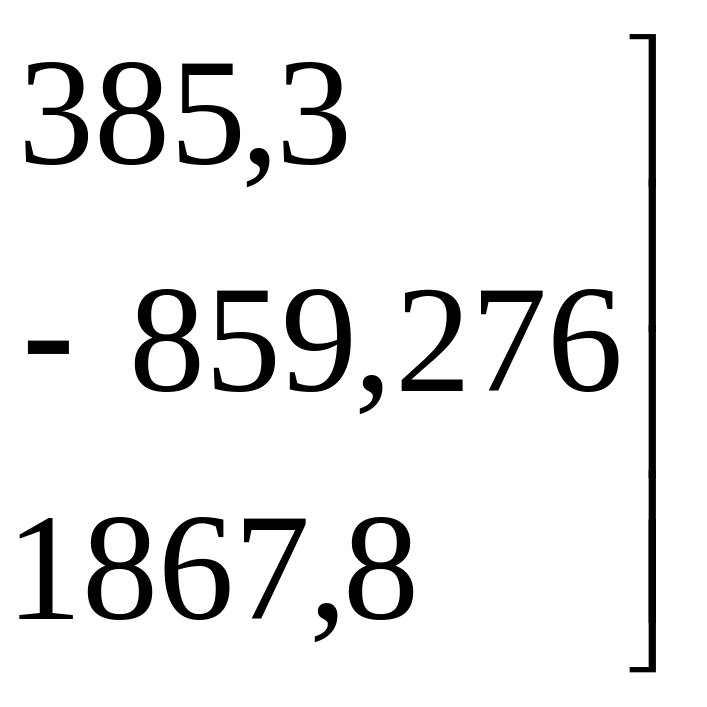Теперь определим значения дисперсий оценок :

(здесь - диагональный элемент матрицы );

;

;

Средние квадратичные ошибки коэффициентов частной регрессии в этом случае будут равны:

Оценим значимость коэффициентов частной регрессии. Для проверки гипотезы , воспользуемся статистикой . Подставив соответствующие значения, получим:

По таблице t-распределения для и при двусторонней критической области находим критическое значение . Поскольку для , коэффициенты регрессии статистически надежны.

Далее определим :

Найдем теперь 95 %-е доверительные интервалы. Для и квантиль . Тогда , или .

Рассчитаем средний квадрат ошибок регрессионной модели:

.

Коэффициент аппроксимации

MAPE .

Данная модель имеет хорошую точность. Оценку адекватности модели сделаем по F-критерию Фишера:

Вектор есть вектор ошибок уравнения регрессии . А произведение . Таким образом, знаменатель

.

Вектор есть вектор значений , вычисленных по уравнению регрессии:

, откуда и

По таблице F-распределения при заданном уровне значимости и и степенях свободы находим . Так как адекватность в целом подтверждается.

Вопросы для самопроверки

1. Как определяется прогноз зависимой переменной по регрессионной модели?

2. Изложите методику построения доверительных интервалов регрессии и прогностической оценки.

Задача. По данным табл. 2.30 вычислите прогностическое значение объема выпуска валовой продукции Y (тыс. ден. ед.) для производительности труда , равной 200 ден. ед./ч, и среднего процента выполнения нормы , равного 101 %.

Т а б л и ц а 2.30

Y				Y
127 4,3 90 129 6,5 100 120 5,1 99 132 6,8 99 125 5,5 103 135 6,9 102 126 6,6 104 135 7,0 103 133 6,2 101 140 7,4 106

10