2.5. Ранговая корреляция

В экономических исследованиях встречаются явления, признакам которых не удается однозначно приписать те или иные абсолютные значения. В таких случаях элементы совокупности располагаются в определенном порядке в соответствии с некоторым признаком, присущим им в неодинаковой мере. Построенный ряд элементов называют упорядоченным, а процесс упорядочения - ранжированием. Каждому члену упорядоченного ряда присваивается ранг или ранговое число (порядковый номер). Например, элементу с наименьшим значением признака приписывается ранг 1, следующему за ним элементу - ранг 2 и т.д. Так происходит сравнение каждого элемента со всеми остальными элементами совокупности. Если элемент обладает не одним, а двум признаками X и Y, то для исследования их влияния друг на друга каждому элементу приписываются два порядковых номера в соответствии с установленным правилом ранжирования. Затем переходят к изучению связи между ранговыми числами путем определения

соответствия между двумя последовательностями порядковых оценок.

Пусть обозначают ранги, соответствующие значениям переменной Y, а - ранги, соответствующие значениям переменной X. Тогда если переменные X и Y имеют различные ранги, то для оценки связи между ранговыми числами, т.е. для измерения тесноты ранговой корреляции, используется коэффициент ранговой корреляции Спирмэна.

,

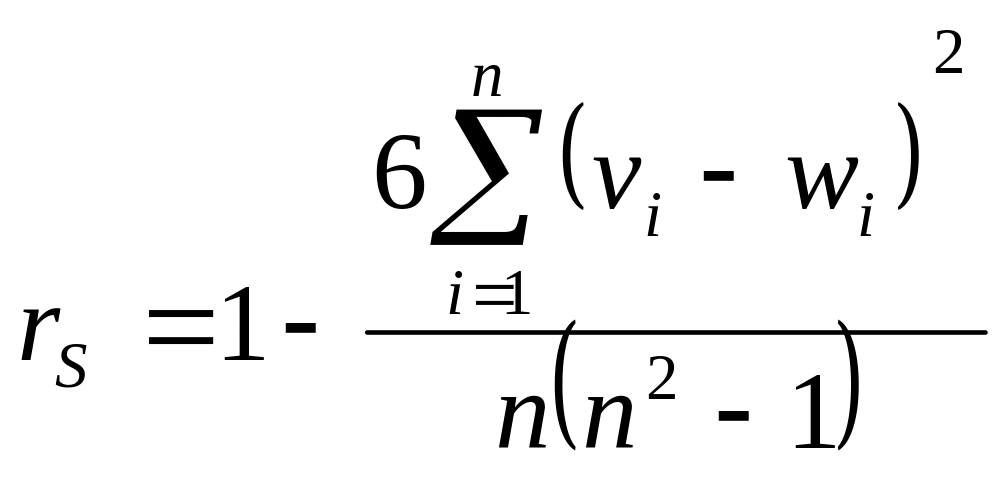где n - объем выборки.

Если же несколько элементов совокупности имеют одинаковые значения одного и того же признака, т.е. обладают свойством отсутствия предпочтений, то каждому такому элементу приписывается ранг, равный среднему арифметическому рангов, если бы они были различимы. Например, если у переменной X третье, четвертое и пятое значения одинаковы по величине, то каждому приписывается ранг, равный среднему арифметическому рангов, если бы они были различимы, т.е. ранг (3 + 4 + 5)/3 = 4. Следующему по величине значению переменной X приписывается ранг 6. Группа элементов, обладающих свойством отсутствия предпочтений, называется связкой, а элементы - связанными. Коэффициент ранговой корреляции Спирмэна при наличии связанных рангов вычисляется по формуле

,

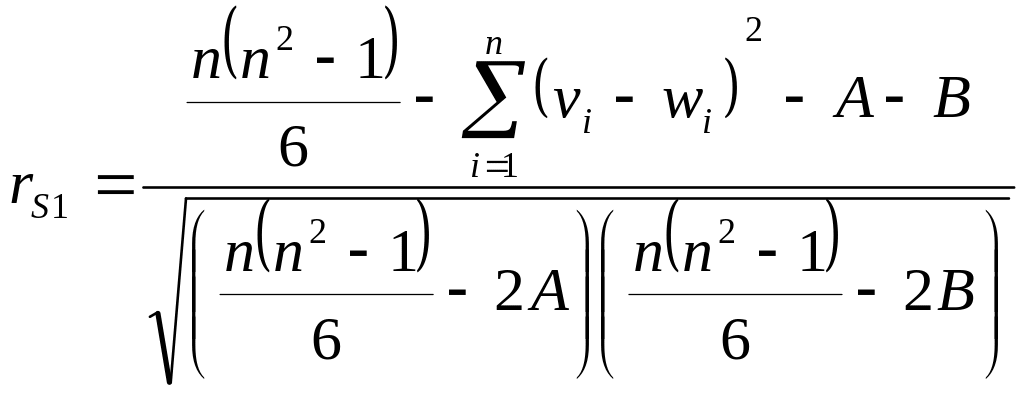где A, B - поправочные коэффициенты для связок в последовательностях v и w рангов соответственно:

; ;

j, k - порядковые номера связок среди рангов v и w; - число одинаковых значений рядов и , принадлежащих одной связке. Например, если имеется одна связка, то , если две, то , и т.д.; если первой связке принадлежат три одинаковых значения, то , если второй связке принадлежат семь одинаковых значений, то , и т.д. Аналогична интерпретация значений для k и .

Коэффициент ранговой корреляции Спирмэна принимает значения внутри интервала . При имеется полная согласованность между элементами двух рядов, т.е. каждый элемент занимает одно и то же место в обоих рядах, что означает полную положительную корреляцию рангов. Если же , то элементы двух последовательностей расположены в обратном порядке и полностью рассогласованы. При корреляция между рангами отсутствует. Достоинство коэффициента ранговой корреляции заключается в том, что он не связан с предположением о нормальности распределения исходных данных. Однако если генеральная совокупность распределена нормально и объем выборки , то коэффициент корреляции связан с коэффициентом ранговой корреляции следующим образом:

.

Другим коэффициентом ранговой корреляции, не связанным с предпосылкой о нормальном распределении изучаемых случайных величин, является  коэффициент  ранговой  корреляции Кендалла,  который можно вычислять по одной из эквивалентных  формул:

или

.

Параметры, входящие в эти формулы, определяют следующим образом. Элементы выборки располагают так, чтобы последовательность рангов одной из переменных представляла собой натуральный ряд чисел 1, 2, 3, .., n, ... Для каждого i-го члена последовательности рангов второй переменной устанавливают числа и отражающие соответственно прямой и обратный порядок расположения последующих рангов. Например, предположим, что ранги образуют натуральный ряд чисел, а . Тогда будет равно числу рангов, которые больше 5, а — числу рангов, которые меньше 5, и т.д. Затем подсчитываем суммы этих чисел и , т.е.

,

и разность полученных сумм . Отметим, что может быть достигнута, когда порядок рангов  в обеих  последовательностях совпадает. Величина изменяется в пределах . Если вычислить и по одной и той же последовательности рангов, то .

Относительно простым показателем степени взаимосвязи двух упорядоченных рядов рангов является индекс Фехнера

,

где v - количество совпадений знаков разностей и ; w - количество несовпадений знаков разностей; - средние арифметические рангов. Если встречаются разности и , равные нулю, то половину из них относят к v, а половину – к w. Значения индекса Фехнера принадлежат промежутку . При между признаками явления корреляция положительная, при - отрицательная, а при связь отсутствует.

Так как индекс Фехнера учитывает только количество совпадений и несовпадений знаков отклонений, то он рекомендуется для приблизительной оценки связи.

Метод  ранговой корреляции предполагает, что функция регрессии, отражающая изучаемую связь между факторами, монотонна.

Ранговую корреляцию применяют: при исследовании зависимости между сортностью продукции, ее сроком службы и производственными затратами; при анкетировании и опросах населения; при обработке результатов психологических и педагогических тестов и т.д. Таким образом, ранговая корреляция используется для изучения связей в тех случаях, когда свойства явления позволяют производить сравнительную оценку, с помощью которой устанавливаются

последовательности рангов.

Пример 2.3. Определим тесноту связи между фондом оплаты труда X (тыс. ден. ед.) и среднемесячной заработной платой Y (тыс. ден. ед.) на предприятиях Министерства жилищного и коммунального хозяйства Республики Беларусь. Данные приведены в табл. 2.22.

Т а б л и ц а 2.22

X	Y		X	Y
16 866,2 1,80 464,33 1,75 16 480,5 1,60 823 1,83 19 786,1 1,60 159,6 1,12 13 060,7 1,45 372,63 1,98 13 763,6 1,50 226,8 1,58 15 639,6 1,59 16,7 2,15 11 483,2 1,39 34,9 1,03 5 928,47 1,70 1 011,9 1,85 2 006,4 2,10 216,9 1,36 1 958,2 1,33 275,87 2,21 859,1 1,38 87,1 3,35 13 615,37 2,31 2 224,6 1,63 137,1 2,32 1 164,8 1,80

Для исследования влияния друг на друга указанных признаков X и Y каждому элементу приписываем два порядковых номера. Значения переменной X располагаем в порядке возрастания, т.е. получаем упорядоченный ряд. Каждому значению признака X присваиваем ранг (числовое число). Первому элементу упорядоченного ряда с наименьшим значением признака присваиваем ранг 1, следующему за ним - ранг 2 и т.д. Соответствующие значения переменной Y при этом располагаются произвольно, но ранжирование их производится согласно установленному правилу - в порядке возрастания. Элементу с наименьшим значением признака Y (1,03) присваиваем ранг 1, следующему за ним по величине (1,12) - ранг 2 и т.д. Полученные ранги значений переменных X и Y укажем в табл. 2.23. Ранги, соответствующие значениям переменной X, обозначим через w, а ранги, соответствующие значениям переменной Y, - через v.

Фонд оплаты труда X, тыс. ден. ед.		Среднемесячная заработная плата Y тыс. ден. ед.		Ранги значений переменных				Число рангов
								распо- ложенных в прямом порядке	распо- ложенных в обрат- ном по- рядке
				X	Y
1		2		3	4	5	6	7	8
- - - - - - - - - - - - - - - - - + + + + + + + + + + + + +	34,9 87,1 137,1 159,6 216,7 216,9 226,9 275,87 372,63 464,33 823 859,1 1 011,9 1 164,8 1 958,2 2 006,4 2 224,6 5 928,47 11 483,2 13 060,7 13 615,37 13 763,6 15 639,6 16 480,5 16 886,2 19 786,1 15 639,6 16 480,5 16 886,2 16 786,1	1,03 3,35 2,32 1,12 2,15 1,36 1,58 2,21 1,98 1,75 1,83 1,38 1,85 1,80 1,33 2,10 1,63 1,70 1,39 1,45 2,31 1,50 1,59 1,6 1,8 1,6 1,59 1,6 1,8 1,6	- + + - + - - + + - + - + + - + - - - - + - - - + - - - + -	1 2 3 4 5 6 7 8 9 10 11 12 131 4 15 16 17 18 19 20 21 22 23 24 25 26 23 24 25 26	1 26 25 2 22 4 9 23 20 15 18 5 19 16,5 3 21 13 14 6 7 24 8 10 11,5 16,5 11,5 10 11,5 16,5 11,5	0 24 22 -2 17 -2 2 15 11 5 7 -7 6 2,5 -12 5 -4 -4 13 -13 3 -14 -13 -12,5 -8,5 -14,5 -13 -12,5 -8,5 -14,5	0 576 484 4 289 4 4 225 121 25 49 49 36 6,25 144 25 16 16 169 169 9 196 169 156,25 72,25 210,25 169 156,25 72,25 210,25	25 0 0 23 2 19 14 1 2 6 3 13 2 2 11 1 3 2 7 6 0 4 3 1 0 0 3 1 0 0	0 24 23 0 19 1 5 17 15 10 12 1 11 9 0 9 6 6 0 0 5 0 0 0 1 0 0 0 1 0
 138 883,67		45,71		351	351		3 224,0	P=150	Q=165

Так как у переменной Y одиннадцатое и двенадцатое значения одинаковы по величине, т.е. являются связанными, каждому из них присваивается ранг, равный 0,5 (11 + 12) = 11,5. Следующему по величине значению (1,63) присваивается ранг 13. У переменной Y шестнадцатое и семнадцатое значения также одинаковы по величине. Каждому связанному значению присваивается ранг, равный 0,5 (16 + 17) = 16,5. Следующему по величине значению (1,83) присваивается ранг 18 и т.д.

Далее от корреляции признаков переменных X и Y переходим к изучению связи между ранговыми числами с помощью коэффициента ранговой корреляции Спирмэна, который вычисляем по формуле (2.33). Прежде чем применить формулу (2.33), вычислим поправочный коэффициент A для связок в последовательности рангов v. Так как в этой последовательности имеются две связки, то j= 1.2. Тогда

где , т.е. первой и второй связкам принадлежат по два одинаковых значения. В этом примере B = 0, так как связок в последовательности рангов w нет.

Коэффициент ранговой корреляции Спирмэна

.

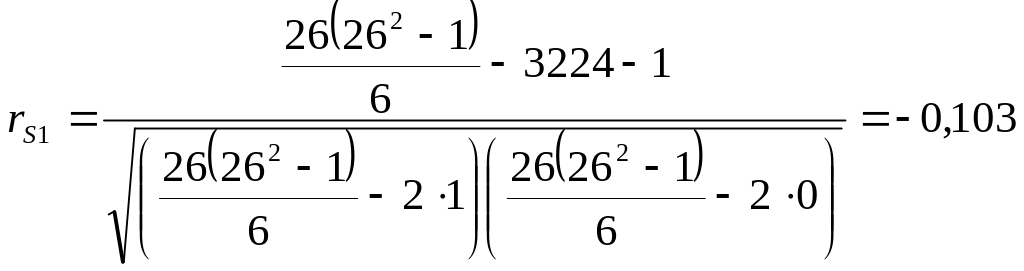Значение свидетельствует о слабой отрицательной связи между фондом оплаты труда и среднемесячной заработной платой на предприятиях Министерства жилищного коммунального хозяйства Республики Беларусь.

Вычислим теперь коэффициент ранговой корреляции Кендалла , также не связанный с предположением о нормальности генеральной совокупности. Результаты промежуточных вычислений приведены в табл. 2.23 (столбцы 7 и 8). Числа и находим, используя последовательность рангов , так как последовательность рангов образует натуральный ряд чисел. За первым числом этой последовательности находится 25 рангов, которые больше 1, и нет ни одного ранга меньше 1. За вторым числом нет ни одного ранга больше 26 и имеется 24 ранга, которые меньше 26, и т.д. Так определяются значения чисел и .

По данным табл. 2.23 получаем значение коэффициента Кендалла:

,

которое подтверждает слабую отрицательную связь между изучаемыми переменными.

Вычислим далее для переменных X и Y средние значения:

и определим знаки отклонений и . Каждая пара наблюдений будет характеризоваться совпадающими или несовпадающими знаками (++; - -; + -; - +). Первая пара наблюдений (34,9; 1,03) характеризуется знаками (- -); вторая пара (87,1; 3,35) - знаками (- +) и т.д. Из табл. 2.23 следует, что количество совпадений знаков v = 10, а количество несовпадений знаков w = 16. Тогда индекс Фехнера

.

Он также подтверждает слабую отрицательную корреляцию между фондом оплаты труда и среднемесячной заработной платой.

Вопросы для самопроверки

1. В каких случаях применяются коэффициенты ранговой корреляции?

2. Как присваиваются ранги значениям признаков X и Y при вычислении коэффициента Спирмэна?

3. Изложите процедуру вычисления коэффициента Кендалла и индекса Фехнера.

Задача. По данным, приведенным в табл. 2.24, вычислите показатели взаимосвязи средней выработки продукции в единицу времени Y (изделий в час) и коэффициентом механизации работ X(%).

Т а б л и ц а 2.24

X	Y		X	Y		X	Y
53 27 72 29 84 40 61 20 75 32 87 41 65 25 78 35 89 42 67 26 80 35 92 44 70 33 81 40