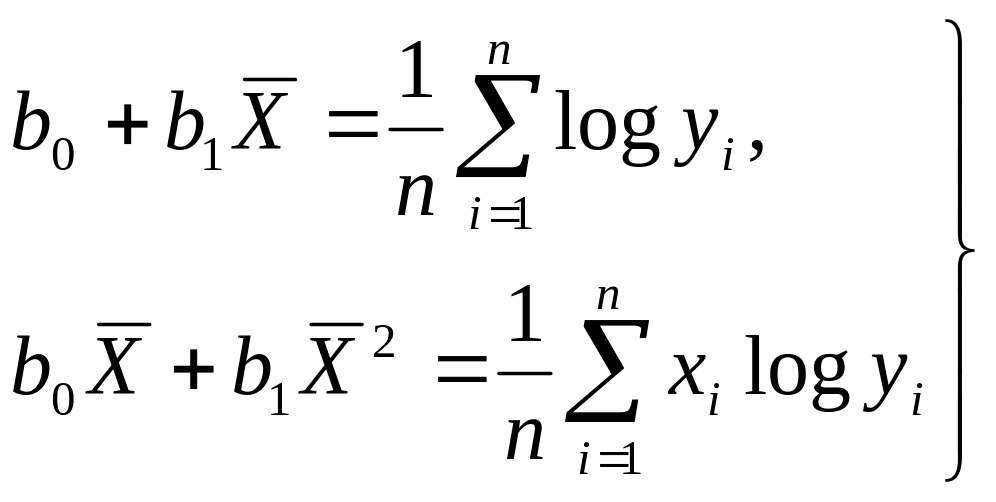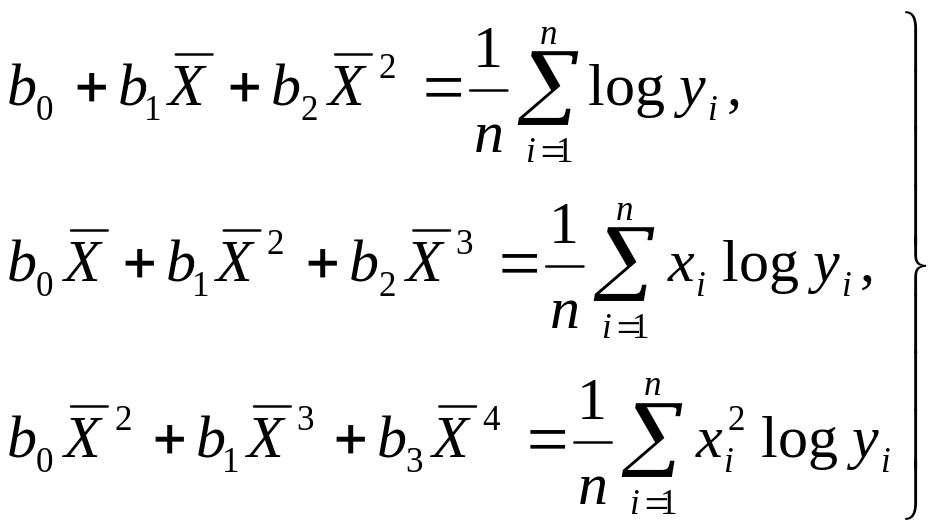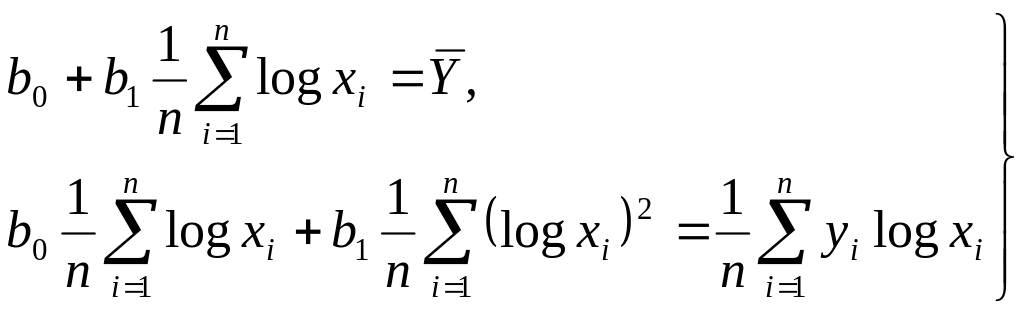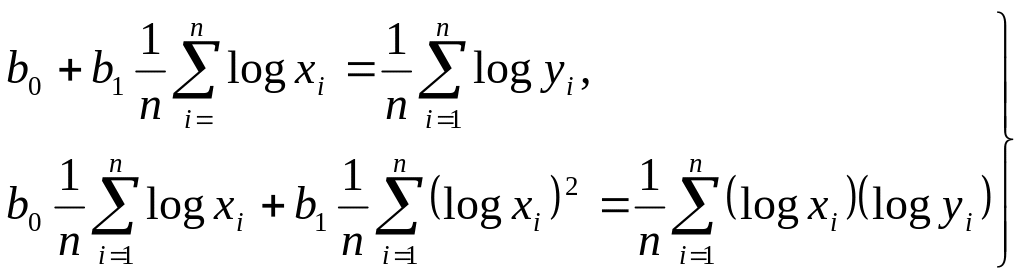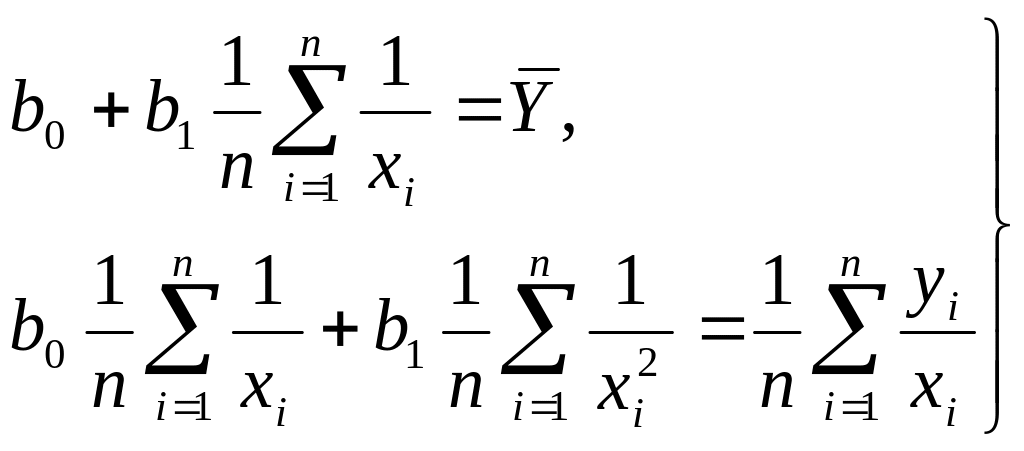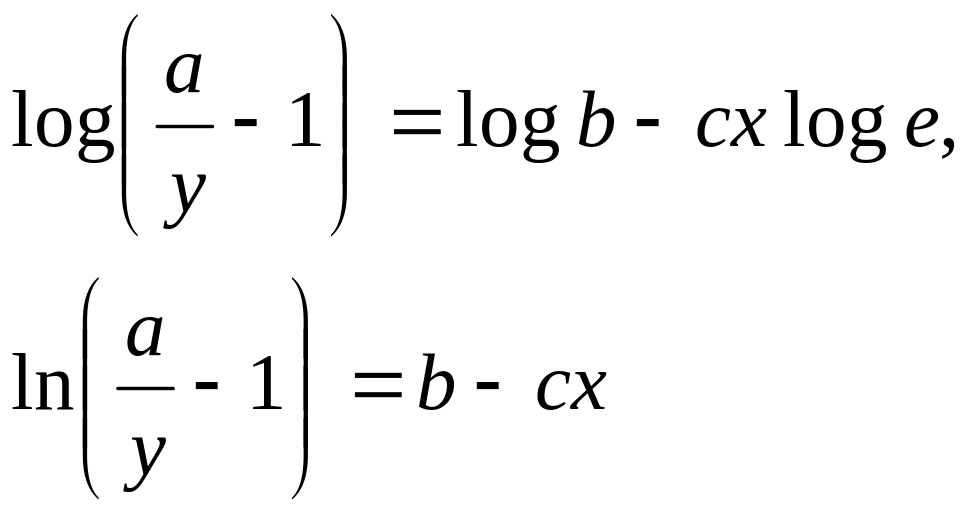2.3. Однофакторные регрессионные модели

Выбор формы однофакторной регрессионной модели. Для более углубленного исследования связей и взаимозависимости экономических явлений статистические методы, изученные в § 2.1, 2.2, дополняются функциями регрессии, которые выражают количественное соотношение между явлением-результатом и явлениями-причинами. Форма связи между экономическими явлениями выражается аналитическим уравнением, на основании которого определяются величины признака (явления), зависящие от фактора или факторов, принимаемых во внимание. При этом нужно определить такое математическое уравнение, которое наилучшим образом описывало бы характер исследуемого экономического процесса. Установление формы связи зависит от характера взаимосвязи исследуемых явлений и определяется тои наукой, к которой относятся изучаемые явления. Если изучается связь между факторным и результативным признаками, то форму этой связи можно определить из расположения точек на корреляционном поле или из корреляционной таблицы, в которой вычисляются средние результативного признака для каждой группы факторного признака:

,

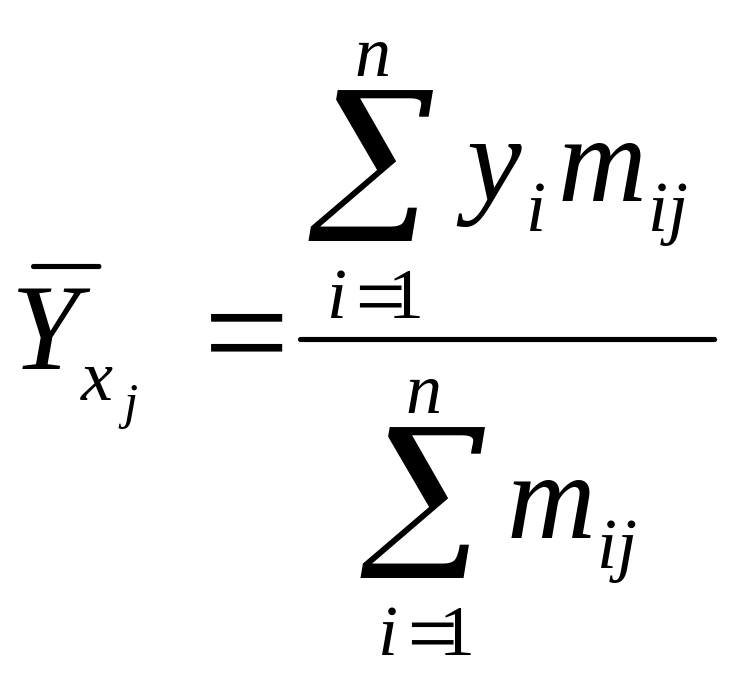где – значения середины интервалов ряда распределения Y; – частоты парных значений и .

Для определения вида функции регрессии, соответствующей реальной форме зависимости, используется метод дисперсионного анализа, который позволяет оценивать линейность регрессии. Покажем, как реализуется метод дисперсионного анализа для случая линейной формы связи. Для этого предположим, что между исследуемыми признаками существует линейная зависимость .

Сгруппируем всю совокупность наблюдений в виде таблицы:

,

где каждая строка соответствует определенному значению фактора X.

Для определения параметров и нужно минимизировать сумму

которую представим в виде

где – эмпирическая линия регрессии. Это разложение приводит к дисперсиям:

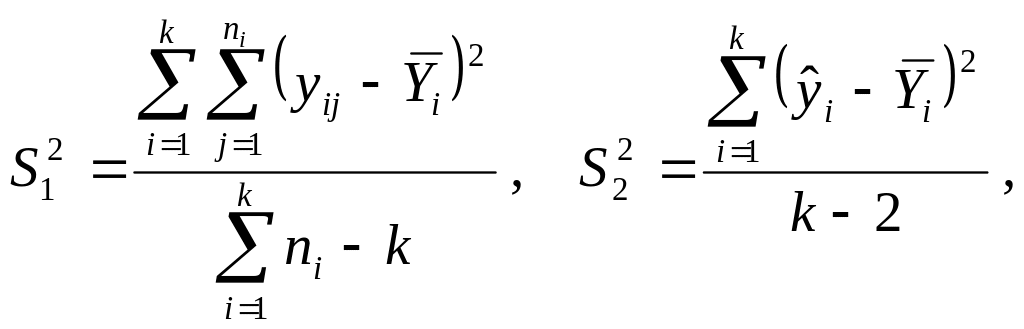
Дисперсии – это вариации значений признака соответственно в пределах групп наблюдений и около линии регрессии; – вариации эмпирических коэффициентов по отношению к теоретическим.

Для проверки гипотезы линейности связи между исследуемыми признаками составляется F -отношение:

,

которое подчиняется распределению Фишера – Снедекора с и степенями свободы. И если вычисленное F-отношение меньше табличного для заданного уровня доверия, то гипотеза о линейности связи подтверждается.

Смысл изложенного ясен. Если регрессия прямолинейная, то отклонения от нее следует считать случайными. Случайной при такой зависимости будет и та часть отклонений, которая приходится на различия между теоретической и эмпирической линиями регрессии. Теоретическая регрессия представляет то предельное положение, к которому стремится эмпирическая регрессия при увеличении числа наблюдений. Расхождение между ними обусловливается тем, что в эмпирической линии регрессии оказывается непогашенной некоторая часть случайных колебаний. Но это верно лишь тогда, когда теоретическая регрессия в виде прямой действительно правильно выражает форму связи. Если же это не так, то и отклонения эмпирической линии регрессии от теоретической прямой регрессии должны уже рассматриваться не как случайные, а как закономерное отражение кривизны регрессии. Сравнение этих отклонений с чисто случайной их величиной и должно дать ответ на поставленный вопрос о линейной регрессии.

Основные предпосылки применения метода наименьших квадратов в аппроксимации связей признаков социально-экономических явлений. Так как при построении регрессионной модели мы не можем охватить весь комплекс причин и учесть случайность, присущую в тои или иной степени причинному действию и определяемому им следствию, то в выражение функции регрессии необходимо ввести аддитивную составляющую – возмущающую переменную U, дающую суммарный эффект от воздействия всех неучтенных факторов и случайностей. Эмпирические значения Y можно вследствие этого представить в виде . Для нахождения параметров расчетных значений Y должны выполняться некоторые предпосылки (предположения). Эти предпосылки имеют общий характер, т.е. они не определяются объемом выборки и числом включенных в анализ переменных.

Наиболее существенными предположениями являются следующие.

1. Полагаем, что для фиксированных значений переменных математическое ожидание возмущающей переменной равно нулю: . Следовательно, средний уровень значений переменной Y определяется только функцией регрессии и возмущающая переменная не коррелирует со значениями регрессии:

.

2. Дисперсия случайной переменной U должна быть для всех одинакова и постоянна: . Это свойство возмущающей переменной U называется гомоскедастичностью.

3. Значения случайной переменной U попарно независимы в вероятностном смысле: для .

4. Число наблюдений должно превышать число параметров (n > m), иначе невозможна оценка этих параметров. Между факторными переменными не должно существовать строгой линейной зависимости, т.е. должна отсутствовать мультиколлинеарность между факторными переменными. При простой линейной регрессии это предположение сводится к условию .

5. Переменные факторы не должны коррелировать с возмущающей переменной U , т.е. . Это значит, что рассматриваемая односторонняя зависимость переменной Y от

переменных , а взаимосвязь отсутствует.

6. Возмущающая переменная распределена нормально. Предполагается, что переменная U не оказывает существенного влияния на переменную Y и представляет собой суммарный эффект от большего числа незначительных некоррелированных влияющих факторов.

Метод наименьших квадратов – один из наиболее распространенных методов оценивания неизвестных параметров регрессии по эмпирическим данным. Существуют и другие методы оценок параметров регрессии. Отметим, что при одних и тех же предположениях и одной и тои же функции регрессии различные способы оценивания приводят к разным оценкам параметров регрессии.

Задача регрессионного анализа состоит в нахождении истинных значений параметров, т.е. в определении соотношения между X и Y в генеральной совокупности. С помощью регрессионного анализа находят оценки параметров регрессии, наиболее хорошо согласующиеся с опытными данными. Разность между значениями параметров регрессии и их оценками возникающая за счет оценивания на основе имеющихся в распоряжении данных, называется ошибкой оценки. При выборе метода оценивания регрессии пытаются найти такие оценки параметров регрессии, относительно которых с достаточно большей вероятностью можно утверждать, что они незначительно отличаются от истинного значения параметра или что они являются несмещенными, состоятельными и эффективными.

Состоятельность – важнейшее и минимально необходимое требование, предъявляемое к оценкам.

Если выполняются предпосылки 1 – 6, то оценки параметров регрессии, полученные методом наименьших квадратов, являются состоятельными, несмещенными и эффективными. Оценки, полученные методом наименьших квадратов, обладают наименьшей дисперсией. В этом смысле они представляют собой наилучшие линейные несмещенные оценки параметров теоретической регрессии.

Построение регрессионной прямой методом наименьших квадратов. Если, исходя из профессионально-теоретических соображений в сочетании с исследованием расположения точек на корреляционном поле или других соображений, предполагают линейный характер зависимости усредненных значений результативного признака, то эту зависимость выражают с помощью функции линейной регрессии, которая служит оценкой линейной функциональной связи между результативным и факторным признаками:

.

На результативный признак оказывает влияние и ряд других факторов. Чтобы элиминировать (сгладить) влияние этих факторов, нужно произвести выравнивание фактических величин Y на основании предположения, что между X и Y существует функциональная зависимость. При этом фактические значения Y заменяются значениями, вычисленными па формуле

. (2.3)

Так как все факторы, кроме фактора X, рассматриваются как постоянные средние величины и выражены параметрами и , то и сглаженные величины Y представляют собой средние . Неизвестные параметры и входящие в уравнение (2.3), определяются методом наименьших квадратов:

.

Величина S является функцией параметров и . Тогда, в силу необходимого условия экстремума, частные производные S по и должны быть равны нулю:

.

Выполнив преобразования и решив систему нормальных уравнений, получим:

,

.

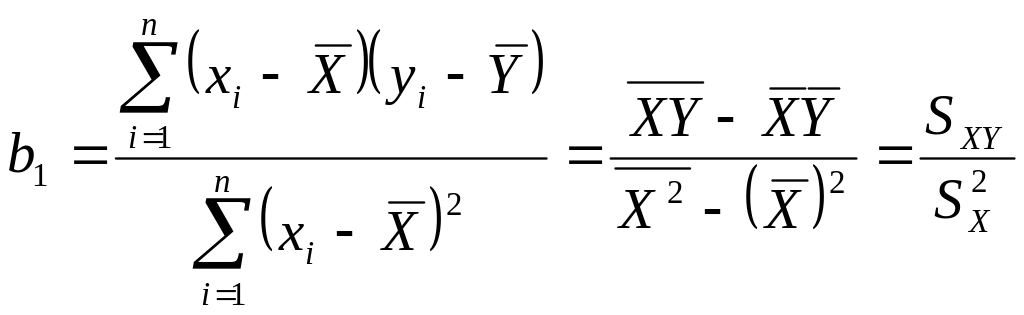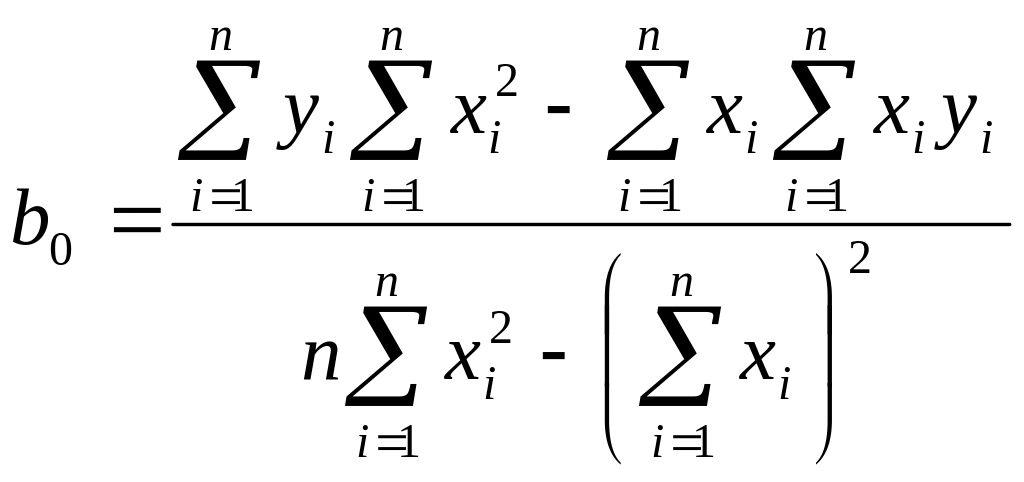Параметр называется коэффициентом регрессии. Он характеризует угол наклона эмпирической регрессии к оси Ox: (рис. 2.3).

Коэффициент регрессии является мерой зависимости переменной Y от переменной X, т.е. указывает, как в среднем изменяется значение переменной Y при изменении переменной X на одну единицу. Знак коэффициента регрессии определяет направление этого изменения.

Отыскание значений коэффициента регрессии представляет большей практический интерес, если ставится вопрос о прогнозе изменений какого-либо показателя в связи с изменением того или иного условия. В частности, коэффициент регрессии используется для определения эластичности спроса и потребления.

В общем случае коэффициент эластичности представляет собой процентное изменение результативного признака при изменении факторного признака на один процент. Он вычисляется по формуле

,

где – коэффициент регрессии; – средние значения соответственно факторного и результативного признаков.

Например, коэффициент эластичности потребления выражает процентное изменение потребления или спроса на данный товар при изменении известных условий (дохода, цены и т.д.) на один процент.

Параметры и прямой регрессии – не безразмерные величины. Постоянная регрессии имеет размерность признака Y. Размерность коэффициента регрессии представляет собой отношение размерности результативного признака к размерности факторного признака.

После вычисления оценок параметров регрессии и , а также средних значений по формуле вычисляем остатки

которые используются в качестве характеристики точности оценки регрессии или степени согласованности расчетных значений регрессии и наблюдаемых значений переменной Y. Для характеристики меры разброса фактических данных вокруг значений регрессии вычисляют дисперсию остатков:

.

Геометрический смысл параметров прямой регрессии следует из рис. 2.2.

Используя дисперсию остатков, можно указать среднюю квадратичную ошибку коэффициента регрессии:

.

Как уже отмечалось, функция регрессии указывает, в какой степени изменяются значения результативного признака в соответствии с изменением факторного признака. Однако этого недостаточно для глубокого изучения их взаимосвязи. Нужно измерить еще интенсивность между изучаемыми факторами. Оценки, полученные с помощью уравнения регрессии, имеют точность тем большую, чем интенсивнее корреляция.

Измерение интенсивности корреляционной связи. Мы рассмотрели, как определяется форма связи между факторным и результативным признаками. Изучим теперь показатели интенсивности этой связи.

Вычислив дисперсию результативного признака и воспользовавшись отклонениями величины от средней величины , получим показатель общей дисперсии , характеризующей вариацию признака Y. Вычислим дисперсию для каждого отдельного значения признака и воспользовавшись отклонениями данных значений от значений, рассчитанных по уравнению линии регрессии, получим условную дисперсию . Она меньше дисперсии .

В качестве показателя интенсивности связи примем нормированное выражение разности этих дисперсий

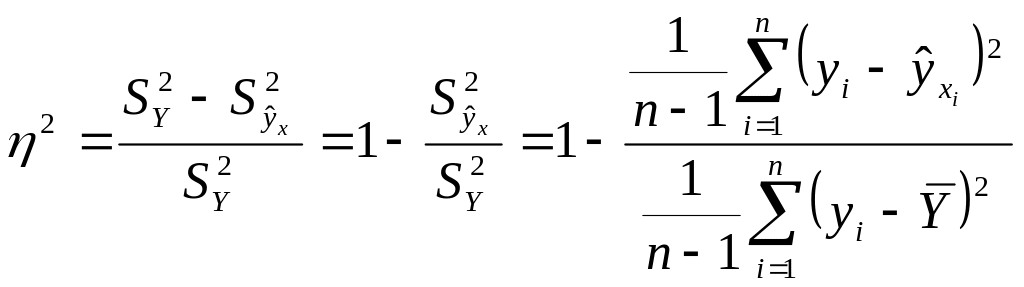
или

. (2.4)

Этот показатель называется корреляционным отношением. При этом чем больше нормированная разность тем теснее связь, т.е. тем теснее фактические данные примыкают к линии регрессии. При функциональной связи все значения Y лежали бы на линии регрессии.

Средняя квадратичная ошибка корреляционного отношения

.

Корреляционное отношение можно вычислять также и по формуле

,

где дисперсия

определяет вариацию величины только вследствие изменения величин т.е. определяет отклонение средних величин , найденных для каждого значения , от общей средней – общая дисперсия признака Y. Таким образом, корреляционное отношение выражает ту часть вариации, которую данный факторный признак составляет в общем действии всех условий вариации коррелируемого с ним другого признака. Но это и определяет тесноту связи, в которой находится признак Y с признаком X.

Корреляционное отношение используется для оценки интенсивности как прямолинейной, так и криволинейной формы связи. Однако оно применяется обычно при криволинейной связи. При прямолинейной связи общим показателем интенсивности является линейный коэффициент корреляции (просто коэффициент корреляции)

.

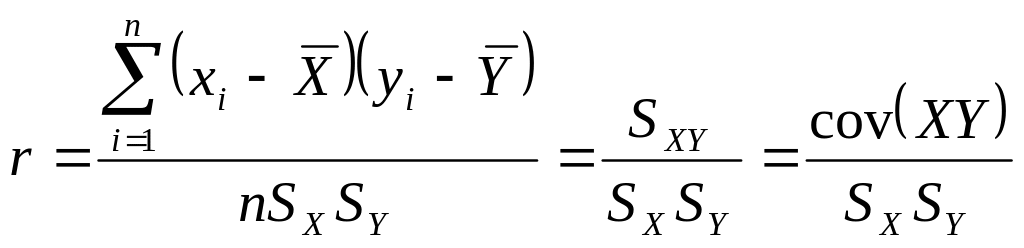Коэффициент корреляции, так же как и корреляционное отношение, является безразмерной величиной, так как сравниваются не индивидуальные отклонения, а нормированные отклонения и . Среднее произведение нормированных отклонений и дает коэффициент корреляции.

Степень интенсивности корреляционной связи можно определить из табл. 2.15.

Т а б л и ц а 2.15

Корреляционная зависимость	Значение коэффициента корреляции
Слабая Умеренная Заметная Тесная Весьма тесная	0,1 < r < 0,3, -0,3 < r < -0,1 0,3 < r < 0,5, -0,5 < r < -0,3 0,5 < r < 0,7, -0,7 < r < -0,5 0,7 < r < 0,9, -0,9 < r < -0,7 0,9 < r < 0,99, -0,99 < r < -0,9

Отметим, что коэффициент корреляции не отражает направление зависимости, т.е. он является функцией, симметричной относительно X и Y.

Средняя квадратичная ошибка коэффициента корреляции определяется по формуле

.

Наряду с коэффициентом корреляции и корреляционным отношением в математической статистике применяется коэффициент детерминации, отражающий, в какой мере функция регрессии определяется факторными признаками, содержащимися в ней.

Для определения коэффициента детерминации дисперсию, характеризующую рассеяние наблюдаемых значений переменной около ее среднего, разложим на две составляющие:

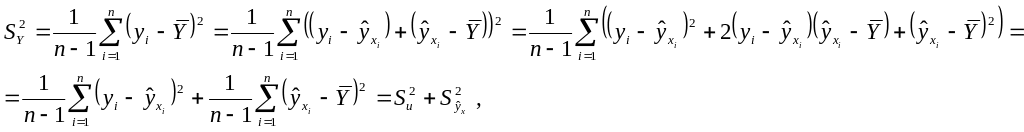
где , так как прямая регрессии проходит через среднюю точку корреляционного поля.

Дисперсия представляет собой ту часть общей дисперсии которая обусловлена случайностью и изменчивостью прочих неучтенных факторов и не объясняется функцией регрессии. Из равенства

видно, что чем меньше , тем меньше эмпирические значения отклоняются от значений регрессии . Вторая составляющая общей дисперсии является дисперсией значений регрессии . Рассеяние значений регрессии определяется значением коэффициента регрессии, следовательно, дисперсия обусловлена влиянием факторного признака. Поэтому чем больше по сравнению с , тем больше общая дисперсия формируется за счет влияния факторного признака и, следовательно, связь между двумя переменными и X более интенсивная. Тогда в качестве показателя интенсивности связи (или оценки доли влияния переменной X на ) используется отношение

,

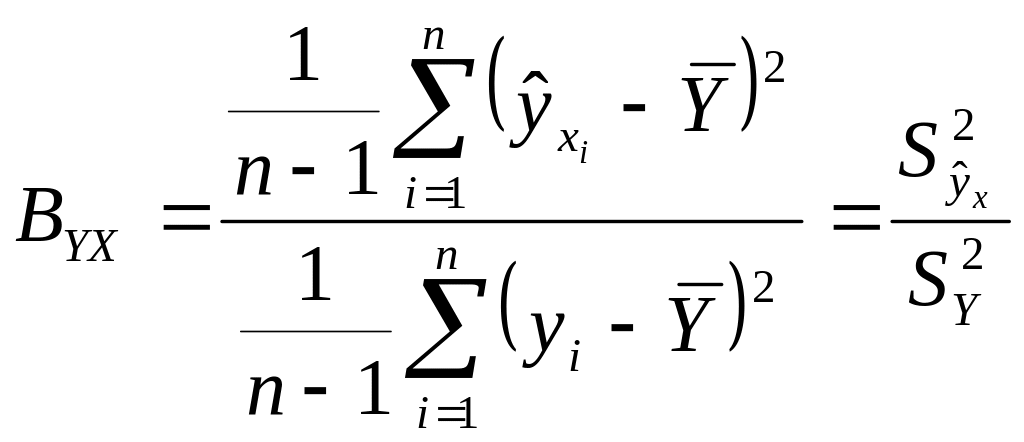которое указывает, какая часть общего рассеяния значений Y обусловлена изменчивостью переменной X, и называется коэффициентом детерминации. Чем большую долю в общей дисперсии составляет , тем лучше выбранная функция регрессии соответствует эмпирическим данным.

Коэффициент детерминации заключен в пределах от 0 до 1 . Если , то все эмпирические значения лежат на регрессионной прямой, т.е. и . В этом случае переменные X и Y связаны линейной функцией. Если , то , а «остаточная» дисперсия равна общей дисперсии , т.е. . В этом случае линия регрессии параллельна оси абсцисс и, следовательно, ни о какой статистической линейной зависимости не может быть речи.

Таким образом, чем больше коэффициент детерминации приближается к единице, тем лучше определена регрессия.

Коэффициент детерминации – величина безразмерная. Она не зависит от единиц измерения признаков X и Y и не изменяется при преобразовании переменных.

Подставляя выражения

в формулу , получаем:

,

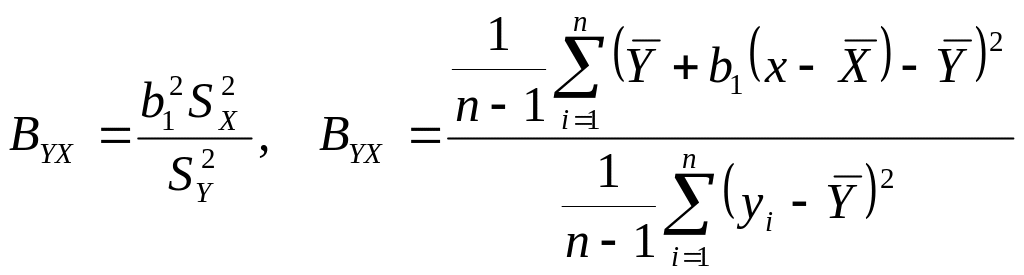откуда, так как

,

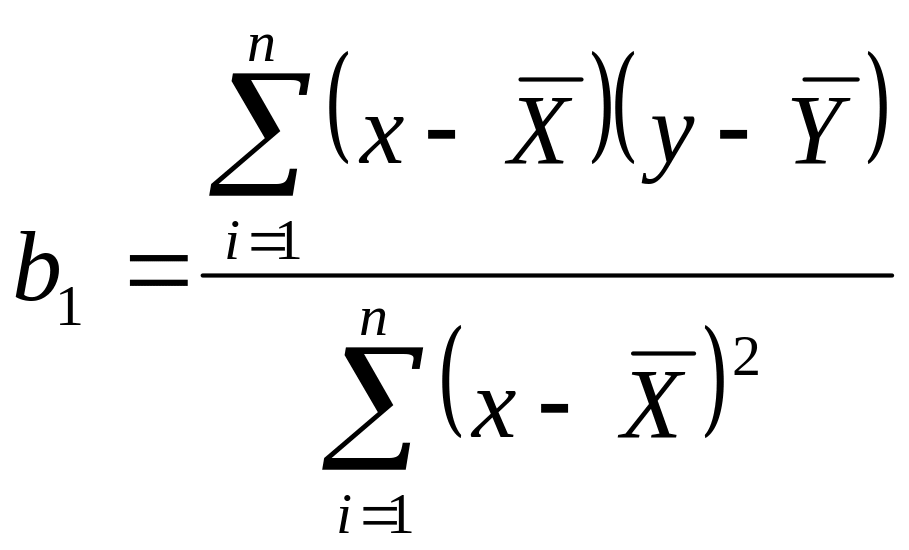выводим формулу коэффициента детерминации, удобную для вычисления:

.

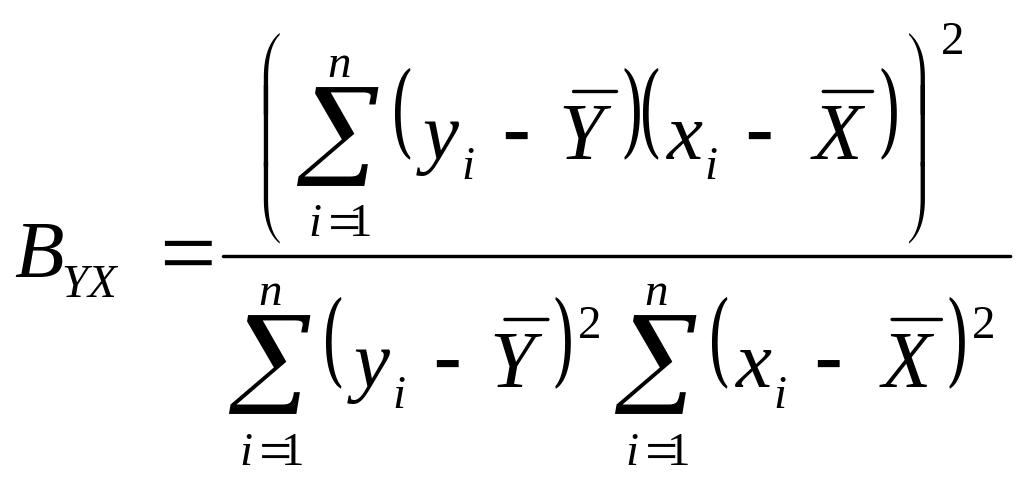Укажем соотношения между коэффициентами корреляции, регрессии и детерминации при однофакторной линейной регрессии:

,

или .

Нелинейная регрессия и корреляция. Подбор функции регрессии должен производиться с применением теории конкретной науки, на базе которой формулируется задача измерения связи между явлениями. При этом следует использовать методы выявления наличия связи. Односторонняя стохастическая зависимость может быть выражена с помощью функций, отличных от линейных.

Различают два класса нелинейных регрессий. К первому классу относятся функции, нелинейные относительно факторного признака, но линейные относительно параметров, входящих в данные функции. Для оценок параметров таких функций применяется метод наименьших квадратов, следовательно, остаются в силе все исходные предпосылки линейного регрессионного анализа. Второй класс регрессий характеризуется нелинейностью факторного признака, входящего в уравнение регрессии.

Т а б л и ц а 2.16

Функция	Нормальные уравнения
1	2
1.
2.
3.
4.
5.	Такие же, как и для функции 2 при замене
6.
7.	Такие же, как для функции 1 при замене
8.	Такие же, как для функции 2 при замене
9.
10.
11.	Такие же, как для функции 1 при замене

Функции, наиболее часто встречающиеся в однофакторных регрессионных моделях, представлены в табл. 2.16 (квазилинейные функции) и 2.17 (нелинейные функции второго класса), где даны также нормальные уравнения для определения входящих в них параметров и преобразованные функции (для нелинейных функций второго класса).

Т а б л и ц а 2.17

Название функции	Аналитическое выражение	Преобразование
Степенная
Показательная
Показательно-степенная
Экологическая
Логистическая
Частный случаи логической функции
Гомперца
Иррациональная
Гиперболическая
Обратная квадратному трехчлену
Дробно-рациональная
Джонсона
Модифицированная экспоненциальная
Торнквиста: 1-го типа
2-го типа
3-го типа

В табл. 2.16 и 2.17 указаны классы регрессий, характеризующихся нелинейностью относительно переменной X или относительно оцениваемых параметров. Квазилинейные функции (см. табл. 2.16) линейны относительно искомых параметров, т.е. их можно представить в виде

, (2.5)

где , – функции переменной X. Они не содержат параметров. Например, или и т.д. Поэтому к функции (2.5) можно применить метод наименьших квадратов. Получим систему нормальных уравнений:

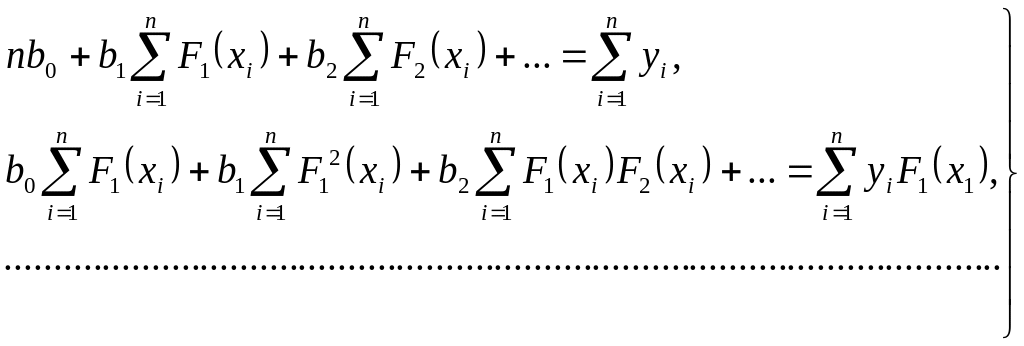
Правило составления нормальных уравнений системы состоит в следующем: первое уравнение системы получается суммированием функций по из уравнения (2.5), остальные уравнения – последовательным умножением функции регрессии (2.5) соответственно на и последующим суммированием полученных результатов по .

Для получения оценок параметров функций из табл. 2.17 их предварительно подвергают преобразованиям, главное назначение которых – линеаризация рассматриваемых зависимостей по оцениваемым параметрам. Параметры регрессии исходных функций находят путем обратных преобразований. Например, путем логарифмического преобразования можно перейти от зависимости показательного типа к линейной .

Применяя метод наименьших квадратов к функции , где , получаем значения и . Потенцируя полученные значения, находим оценки параметров исходной функции. К этому вопросу мы еще вернемся в гл. 3.

Для оценки интенсивности нелинейной связи используется корреляционное отношение (2.4) или индекс корреляции который вычисляется по формуле

.

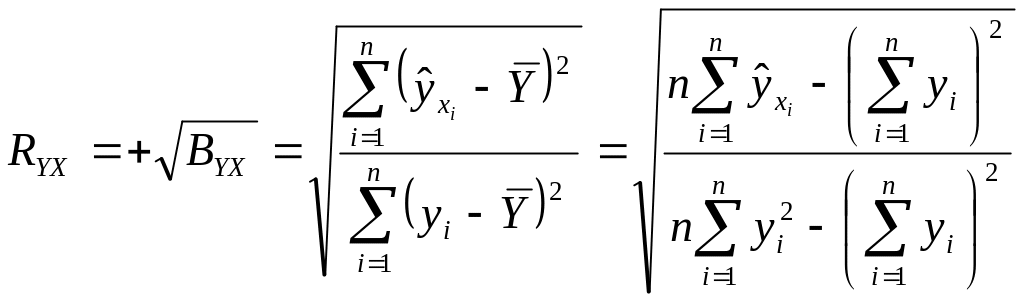Индекс корреляции принимает значения в интервале . Если , т.е. для всех , то мы располагаем функциональной зависимостью. Если же , т.е. для всех , , то связь в этом случае отсутствует. Чем больше значение индекса корреляции приближается к единице, тем сильнее наблюдаемая связь.

Различные уравнения регрессии, служащие для оценки уровня величин исследуемых зависимых переменных, представляют большей практический интерес, например в планировании. Оценки, полученные в уравнении регрессии, достаточно точно воспроизводят линию реальной эволюции явлений, если не слишком отдаляться от эмпирических данных. Экстраполяция допускается только тогда, когда доказана полная аналогия условий, места, времени и однородности явлений, к которым относятся оценки.

Проверка существенности оценок параметров регрессии, коэффициентов корреляции и детерминации. Мы отмечали, что оценки параметров регрессии являются случайными величинами с определенными распределениями вероятностей. При выполнении предположений 1 – 6, указанных выше, оценки параметров регрессии и распределены нормально с математическим ожиданием , и дисперсией . Отсюда следует, что величина имеет стандартное нормальное распределение. Значения распределений оценок параметров регрессии позволяют производить оценку значимости соответствующих статистических характеристик. При практических исследованиях проверка значимости основывается на выборочных наблюдениях. Как всякая статистическая характеристика, параметры уравнения регрессии являются величинами случайными, т.е. их значения случайно рассеиваются вокруг одноименных параметров генеральной совокупности (истинных значений параметров теоретической регрессии). Если значения оценок параметров эмпирической регрессии попадают в зону рассеяния, обусловленную случайным характером самых показателей, это не является доказательством отсутствия регрессионной связи. Можно только утверждать, что исходные данные не отрицают отсутствия связи между переменными. Но если значения оценок параметров регрессии будут лежать вне этой зоны рассеяния, то можно считать, что между переменными существует статистически значимая связь. Используемый для решения этой задачи критерий значимости основан на распределении различных статистик.

Практически проверка значимости начинается с формулировки нулевой гипотезы состоящей в том, что между параметром выборки и параметром генеральной совокупности нет существенного различия. Альтернативная гипотеза утверждает, что между этими параметрами имеется существенное различие. Затем устанавливается уровень значимости , выражающий вероятность того, что нулевая гипотеза отвергается в то время, когда она в действительности верна. При проверке существенности параметров корреляционно-регрессионной связи выборочную характеристику, вычисленную по результатам наблюдений, сравнивают с соответствующим критическим значением. При этом следует различать одностороннюю и двустороннюю критические области. Форма задания критической области зависит от постановки задачи. Если требуется оценить абсолютную величину расхождения между параметрами выборки и генеральной совокупности, то используется двусторонняя критическая область. Если же требуется установить, что один из параметров строго больше или меньше другого, то используется односторонняя критическая область. Уровень значимости при использовании односторонней критической области меньше, чем при использовании двусторонней. В случае симметричного распределения выборочной характеристики уровень значимости двусторонней критической области равен , а односторонней . Более подробное теоретическое обоснование проверки статистических гипотез можно найти в пособии (2, § 8.1).

Рассмотрим критерии значимости для параметров корреляционно-регрессионного анализа. Для оценки каждого параметра регрессии выдвинем следующие гипотезы:

– переменная X не оказывает существенного влияния на зависимую переменную Y;

– переменная X оказывает существенное влияние на зависимую переменную Y.

При такой альтернативной гипотезе используется двусторонняя критическая область. Если же альтернативная гипотеза формулируется в виде : , т.е. имеется значимая положительная (отрицательная) зависимость переменной Y от переменной X, то используется односторонняя критическая область. Ясно, что при такой формулировке альтернативной гипотезы на основании экономических соображений должен быть априори известен знак параметра регрессии.

Для проверки гипотезы используется статистика

, (2.6)

а гипотезы – статистика

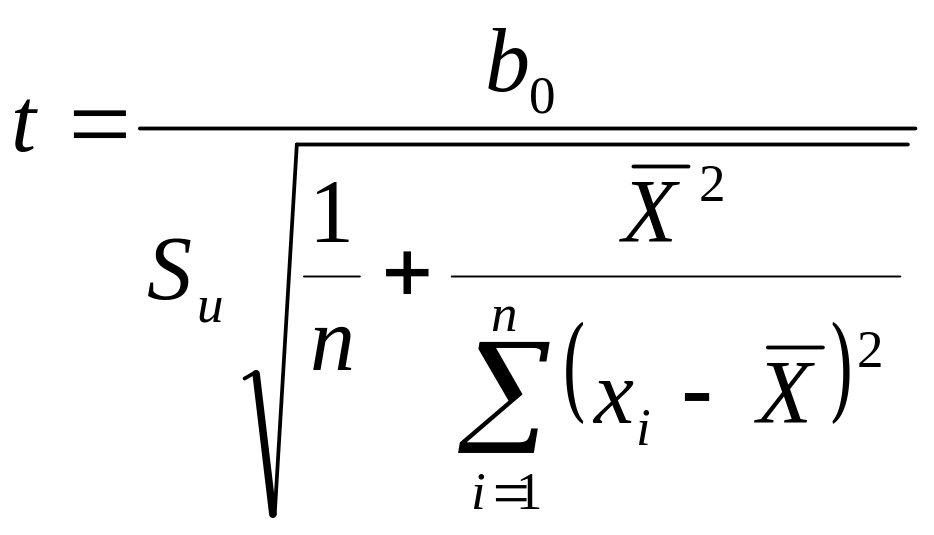, (2.7)

подчиняющиеся распределению Стьюдента с степенями свободы.

Проверяя значимость коэффициента парной корреляции, устанавливают наличие или отсутствие корреляционной связи между исследуемыми экономическими явлениями. При этом выдвигаются следующие гипотезы:

– между переменными X и Y отсутствует значимая корреляционная связь;

– между переменными Y и X имеется существенная корреляционная связь.

Из альтернативной гипотезы следует, что нужно воспользоваться двусторонней критической областью.

Для проверки гипотезы по результатам выборки используется статистика

, (2.8)

распределенная по закону Стьюдента с степенями свободы.

Вычисленные по результатам выборки статистики (2.6) – (2.8) сравниваются с критическим значением, определенным по таблице распределения Стьюдента при заданном уровне значимости и степенях свободы. Если , то нулевая гипотеза отвергается, т.е. корреляционно-регрессионная связь между переменными Y и X значима; если же , то гипотеза об отсутствии связи не вызывает возражений.

Значимость коэффициента корреляции можно определить, если воспользоваться критическими значениями коэффициента корреляции

.

Существуют подробные таблицы критических значений коэффициента корреляции. При этом, если , можно утверждать, что связь между переменными существенная; если же , то нет причин на основании выборки отклонить нулевую гипотезу об отсутствии связи.

В случае, если при формулировке гипотезы нельзя предположить, что коэффициент корреляции генеральной совокупности и, следовательно, нельзя положить , применяют z – преобразование Фишера

к статистике t и получают статистику

,

которая имеет t-распределение с степенями свободы. Процедура проверки значимости проводится далее аналогично предыдущей.

Иногда возникает необходимость проверки гипотезы об отличии друг от друга двух коэффициентов корреляции. При этом предполагается, что рассматриваются одни и те же признаки однородных совокупностей: данные представляют собой результаты независимых испытаний и применяются коэффициенты корреляции одного типа (коэффициенты парной или частной корреляции при исключении одинакового количества переменных). Объемы двух выборок могут быть различны. Нулевая гипотеза формируется в виде (коэффициенты корреляции двух рассматриваемых совокупностей равны). Альтернативная гипотеза состоит в том, что . Для проверки нулевой гипотезы используется статистика

,

где – значения z-преобразования Фишера коэффициентов корреляции и ; – объемы выборок.

Если ( = 0,05 или = 0,01), то гипотеза отвергается. В противном случае, т.е. при , гипотеза принимается. В случае принятия гипотезы величина

после преобразования

tank

может служить свободной оценкой коэффициента корреляции . Затем проверяется гипотеза состоящая в том, что , с помощью статистики

имеющей нормальное распределение.

Для проверки значимости коэффициента детерминации выдвигаются следующие гипотезы:

– переменная X, включенная в регрессию, не оказывает существенного влияния на зависимую переменную;

– выборочный коэффициент детерминации существенно больше коэффициента детерминации генеральной совокупности .

В этом случае для проверки гипотезы следует использовать одностороннюю критическую область. Для оценки значимости парного коэффициента детерминации используется статистика

,

имеющая F-распределение Фишера с и степенями свободы.

Значение статистики, вычисленное по результатам выборки, сравнивается с критическим значением , найденным по таблице F-распределения Фишера при заданном уровне значимости и соответствующем числе степеней свободы. Если , то вычисленный коэффициент парной детерминации значимо (с вероятностью ) отличается от нуля.

Оценка адекватности регрессионной модели. Для подтверждения факта непротиворечивости формы зависимости опытным данным либо опровержения предложенного вида зависимости как не соответствующей этим данным разработаны различные статистические критерии.

Проверим линейность регрессии, используя следующий прием.

Пусть – групповое среднее, соответствующее -му значению переменной X, вычисляемое по формуле

,

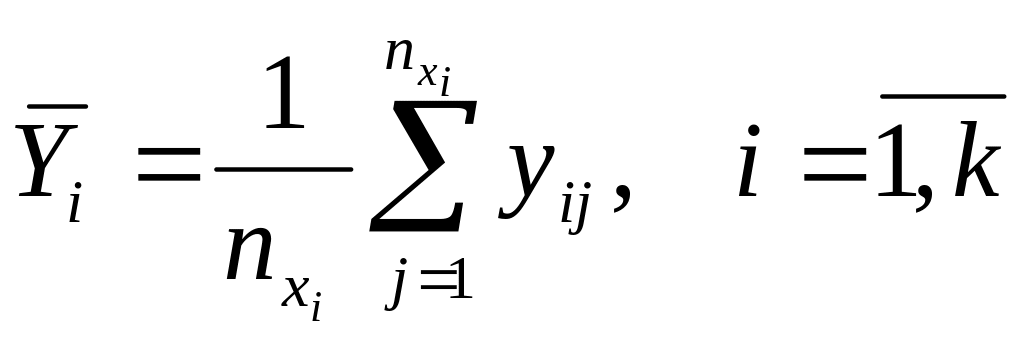где – число значений переменной Y, относящихся к .

Как отмечалось, сумма

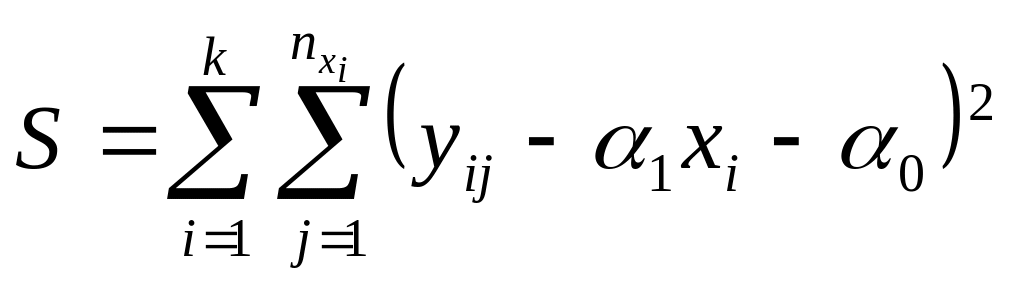
представляется в виде четырех слагаемых: . Тогда если в генеральной совокупности существует линейная регрессия и условные распределения переменной Y хотя бы приблизительно нормальны, то отношение средних квадратов отклонений

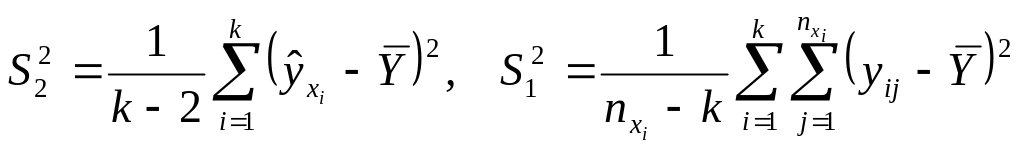(2.9)

имеет F-распределение с и степенями свободы. Значение F, вычисленное для корреляционной таблицы по формуле (2.9), сравнивается с критическим , найденным по таблице при заданном уровне значимости и степенях свободы. Если , то линейная регрессионная зависимость не противоречит опытным данным. В противном случае, т.е. при , гипотеза о линейной зависимости между переменными несостоятельна.

Для проверки статистической адекватности уравнения регрессии обычно используют три метода:

1) проводят анализ дисперсии зависимой переменной Y;

2) определяют стандартную ошибку по формуле

;

3) вычисляют среднюю абсолютную процентную ошибку аппроксимации:

.

Анализ дисперсии зависимой переменной состоит в том, что сумма представляется в виде суммы двух слагаемых:

.

Затем составляется отношение средних значений этих сумм:

,

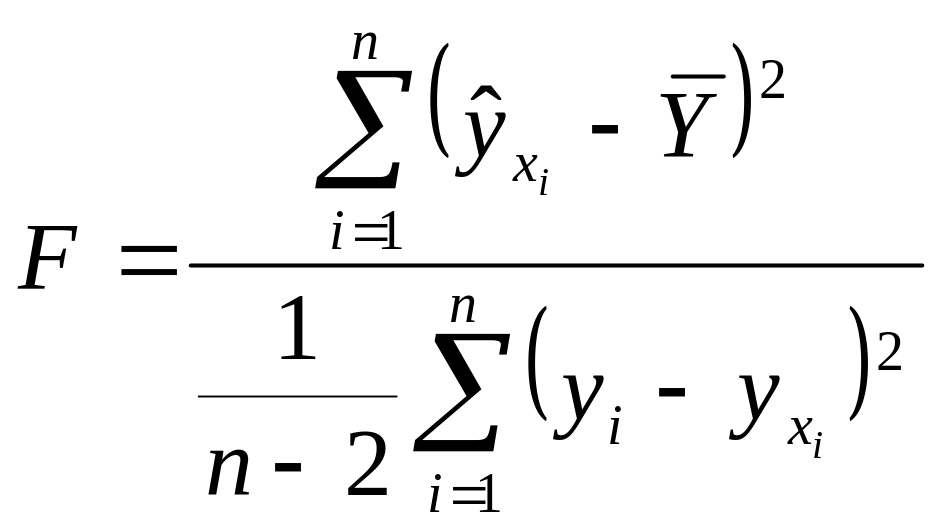которое используется в качестве статистики для проверки гипотезы , состоящей в том, что . Эта выборочная статистика характеризуется F-распределением с и степенями свободы. По таблице F-распределения для заданного уровня значимости и числа степеней свободы и находим квантиль , с которым сравниваем . Если , то уравнение регрессии признается значимым, т.е. доля вариации, отнесенная за счет уравнения регрессии, больше, чем за счет случайных неучтенных факторов. Считается, что уравнение регрессии адекватно изучаемому экономическому процессу, если в 4 раза больше квантиля F-распределения.

Построенное уравнение регрессии можно использовать для прогнозирования значений зависимой переменной по значениям переменной X. Ясно, что действительные значения Y рассеяны вокруг линии регрессии. Первым и наиболее очевидным фактором, во многом определяющим надежность получаемых по уравнению регрессии прогностических оценок, является рассеяние наблюдений вокруг линии регрессии. В качестве меры рассеяния принимается величина

.

Она является выборочной оценкой дисперсии случайных чисел , содержащихся в теоретической модели . Ясно, что чем меньше , тем модель будет более адекватной изучаемому экономическому явлению.

Средняя абсолютная процентная ошибка характеризует в процентах среднее отклонений значений зависимой переменной Y от уравнения регрессии. Модель считается адекватной, если не превосходит 20%.

Чтобы иметь полную уверенность в адекватности модели, нужно выполнить проверку случайности остатков . Методика проверки случайности изложена в § 3.8.

Построение однофакторной регрессионной модели. Исследуем зависимость выпуска валовой продукции на одного среднегодового работника сельского хозяйства (Y , день. ед.) от фондовооруженности одного работника, занятого в сельскохозяйственном производстве (X, тыс. ден. ед. на человека), по данным 30 колхозов Республики Беларусь (табл. 2.18). Из экономических соображений фондовооруженность выбрана в качестве факторного признака.

Т а б л и ц а 2.18

X	Y		X	Y		X	Y
14,482 14,397 12,280 10,397 14,888 12,012 12,819 12,626 13,444 15,043	10532 11079 8698 7032 12805 8854 10702 9089 9332 11982		17,627 14,470 13,096 14,449 16,526 14,389 16,479 14,678 15,995 11,472	13037 9643 8358 11208 11471 12258 13558 10722 10535 9956		13,837 14,153 15,957 16,804 13,752 13,795 15,420 18,342 13,642 19,856	9903 11050 9886 11423 9145 8307 10625 11791 8744 11776

Предположим линейную связь между переменными. Прямую регрессии построим, используя ПЭВМ (программа АРМС). Оцениваемую линейную корреляционную связь можно представить в виде эмпирического уравнения регрессии:

.

Проверим значимость коэффициента регрессии . Для этого выдвинем гипотезу состоящую в том, что переменная X не оказывает существенного влияния на зависимую переменную Y, против гипотезы . Статистика

.

По таблице t-распределения для уровня значимости = 0,05 и степеней свободы находим критическое значение статистики: (при двусторонней критической области). Так как , то переменная X оказывает существенное влияние на Y.

В рассматриваемом примере коэффициент регрессии показывает, что валовая продукция в среднем возрастает на 541,4 ден. ед., если фондовооруженность увеличивается на 1 тыс. ден. ед. . Итак, коэффициент регрессии отражает влияние изменения уровня фондовооруженности на объем выпуска валовой продукции.

Оценим интенсивность связи между фондовооруженностью и объемом выпуска валовой продукции, используя коэффициент корреляции. Так как коэффициент линейной корреляции , между изучаемыми факторами существует тесная корреляционная связь.

Проверим значимость коэффициента корреляции, выдвинув нулевую гипотезу : различие между r и незначимо, и альтернативную гипотезу : различие между r и значимо. Вычисленную по результатам выборки статистику

сравним с критическим значением, определенным по таблице распределения Стьюдента при заданном уровне значимости и степенях свободы: (воспользовались двусторонней критической областью). Так как , то гипотеза отвергается на уровне значимости 0,05. С вероятностью можно утверждать, что между фондовооруженностью и объемом выпуска валовой продукции существует тесная корреляционная зависимость.

Исследуем адекватность построенной однофакторной модели изучаемому экономическому процессу. Вычисленное по результатам выборки F-отношение равно . Сравниваем его с квантилем табличного F-распределения, определенного при уровне значимости и и степенях свободы: . Так как , то уравнение регрессии с вероятностью признается значимым.

Используем остатки в качестве характеристики степени согласованности расчетных значений регрессии и наблюдаемых значений переменной Y.

Подставив в полученное уравнение регрессии значения из табл. 2.18, вычислим значения регрессии и остатки .

Стандартная ошибка остатков рассматривается как стандартная ошибка оценки регрессии в связи с интерпретацией возмущающей переменной U как результата ошибки спецификации функции регрессии. Находим несмещенную оценку дисперсии возмущающего воздействий :

,

.

Из значений остатков следует, что необходимо прежде всего проанализировать деятельность колхозов с номерами 26, 4, 13, 23, 29, 30, 5, 16, 17 и 7, показатели которых отличаются большими отклонениями в ту и другую стороны от значений, предсказанных по уравнению регрессии. В колхозах, для которых обнаружены отрицательные отклонения фактических значений от расчетных, следовало бы уделить особое внимание экономической и организационной работе.

Среднеабсолютная процентная ошибка, вычисленная для данных рассматриваемого примера,

,

что значительно меньше 20%.

Для определения того, какая часть полного рассеяния значений Y обусловлена изменчивостью переменной X, вычислим коэффициент детерминации. Так как , делаем вывод, что только 50,6% общей дисперсии объема выпуска валовой продукции в рассматриваемых колхозах обусловлено вариацией фондовооруженности. Это значит, что в регрессионную модель нужно вводить дополнительные факторы, оказывающие влияние на объем выпуска валовой продукции. Коэффициент неопределенности , или 49,4%. Следовательно, 49,4% общей дисперсии нельзя объяснить зависимостью объема выпуска валовой продукции от фондовооруженности.

Таким образом, из анализа всех показателей адекватности модели следует, что уравнение регрессии статистически значимо, но в построенную модель следует ввести еще ряд факторов, влияющих на объем выпуска валовой продукции.

Вопросы для самопроверки.

1. Как производится выбор формы однофакторной регрессионной модели?

2. Укажите основные предпосылки применения метода наименьших квадратов для нахождения оценок параметров модели.

3. Объясните экономический смысл уравнения регрессии, коэффициентов регрессии, коэффициентов эластичности.

4. Как вычисляется средняя ошибка уравнения регрессии?

5. С помощью какого показателя измеряется интенсивность корреляционной связи?

6. Изложите процедуру проверки значимости параметров регрессионной модели.

Задача. Построите регрессионную модель, характеризующую связь между темпом роста выпуска валовой продукции и темпом роста производительности труда по отраслям промышленности. Соответствующие данные приведены в табл. 2.19.

Т а б л и ц а 2.19

Отрасль	Среднегодовой темп роста, %
	валовой продукции	производительность труда
Энергетика Черная металлургия Машиностроение и металлообработка Химическая Строительные материалы Лесозаготовительная и деревообрабатывающая Бумажно-целлюлозная Текстильная Пищевая Полиграфическая	17,5 14,6 19,8 22,5 15,6 21,1 21,6 9,3 8,9 14,0	11,9 8,1 13,2 4,3 10,4 7,7 5,8 5,7 5,6 8,4