Диагностическая контрольная работа

по алгебре и началам анализа

«Производная функции. Приложения производной»

Вариант 1

Запишите вариант правильного ответа заданий уровня А

^{А1. Найдите производную функции y=9 - 9x8 - x5}

а)9x-x9- x6

б)9x-72x7-5x4

в)-72x7-6x4

г)-17x7-6x4

А2. Найдите производную функции y=(4-3x)⁵ .

а)20(4-3x)4

б)5(4-3x)4

в)-15(4-3x)4

г)-5(4-3x)4

А3. Укажите функцию, являющуюся первообразной для функции f(x)= , при x>0.

а)-

б)

в)2lnx

г)ln2x

А4. Найдите производную функции f(x)=xcos x.

а) cos x

б) -sin x

в) cos x+x·sin x

г)cos x-x·sin x

А5. Найдите значение производной функции f(x)=3x²-6lnx в точке x₀=1.

а) 6

б) 0

в) 3

г) -3

А6. Найдите значение производной функции f(x)=x² sin x в точке x₀= .

а)-

б)

в)-2

г)2

А7. Найдите угловой коэффициент касательной к графику функции

f(x)= x³-2x+7 в точке с абсциссой x₀=3.

а) 7

б) 18.75

в) 10

г) -1

А8. Найдите тангенс угла наклона касательной к графику функции y=x⁴+sin x в точке с абсциссой равной 2.

а)32+cos2

б)32-cos2

в)16ln2+cos2

г)2cosx-

А9. Значение функции y=x³-2x²-4x-1 в точке минимума равняется

а)-

б)2

в)-9

г)-

А10. Найдите наименьшее значение функции y= -x²-3x-1 на отрезке [-3;1].

а) -3

б)

в) -10

г) -12

А11. Найдите площадь фигуры, ограниченной линиями x=0, x= , y=0, y=cos x.

а)

б)

в)1-

г)

А12. Сколько экстремумов имеет функция у= - +5х -1?

а) 2

б) 0

в) 1

г) 3

Запишите решение заданий уровня в с полным обоснованием

В1. Точка движется по координатной прямой согласно закону х(t)=-5+7t-е , где х(t) – координата точки в момент времени t. Найдите скорость точки при t=3.

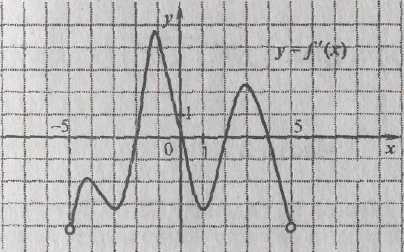
В2. Функция у=f(x) задана на промежутке (-5;5). График ее производной

у= (х)изображен на рисунке. Определите наибольшее из тех значений х , при которых функция имеет минимум.

В3. Для функции f(х)= +х +х найдите первообразную, график которой проходит через точку (1;3).

Запишите решение заданий уровня С с полным обоснованием

С1. К графику функции f (х)=х -4х проведена касательная в точке М(1;-3). Найдите абсциссу точки пересечения касательной с осью Ох.

С2. Число 18 представьте в виде двух положительных слагаемых таких, что сумма их квадратов принимает наименьшее значение.

Диагностическая контрольная работа

по алгебре и началам анализа

«Производная функции. Приложения производной»

Вариант 2

Запишите вариант правильного ответа заданий уровня А

А1. Найдите производную функции f(x)=sin x-cos x.

а) cos x-sin x

б) cos x+sin x

в) -cos x-sin x

г) sin x-cos x

А2. Найдите производную функции y=(-2x+3)⁸

а) -16(-2x+3)7

б) -24(-2x+3)7

в) 8(-2x+3)7

г) -8(-2x+3)7

А3. Укажите функцию, являющуюся первообразной для функции f(x)=x²-10x.

а) -5x2

б) x3-10x2

в) -10x2

г) 2x-10

А4. Найдите значение (2), если f(x)=lnx- .

а) -ln2

б) 0

в) -

г)

А5. Найдите производную функции g(x)= .

а) -

б)

в)

г)

А6. Найдите производную функции y=3x²cos x.

а) -6xsin x

б) 6xcos x-3x2sin x

в) x3cos x+3x2sin x

г) 6xcos x+3x2sin x

А7. Найдите угловой коэффициент касательной к графику функции

f(x)=x³-3x²-11 в точке с абсциссой x₀=2.

а) 0

б) -11

в) -15

г) -26

А8. Найдите тангенс угла наклона касательной к графику функции y=3lnx в точке с абсциссой равной 3.

а) 3ln3

б)

в) 1

г) 3

А9. Значение функции y= - -3x-2 в точке минимума равняется

а) -

б) -

в) -2

г) 3

А10. Сколько экстремумов имеет функция у=- - +5х -1?

а) 2

б) 3

в) 1

г) 4

А11. Найдите площадь фигуры, ограниченной графиком функции у=х -4х+5, прямыми х=1, х=4 и осью абсцисс.

а)

б) 6

в) 18

г) 48

А12. Найдите наибольшее значение функции у=2cosх-14.

а) -16

б) 2

в) -14

г) -12

Запишите решение заданий уровня в с полным обоснованием

В1. Наблюдение за космическим телом показало, что расстояние S(в километрах) между ним и Землей измеряется по закону S(t)=1,8·10 +0,5·10 , где t – время в секундах от момента начала наблюдения. Через сколько секунд после начала наблюдения скорость удаления тела от Земли составит 10 км/с?

В2. Функция у=f(х) определена на промежутке (-8;5). График ее производной изображен на рисунке. Найдите промежутки возрастания функции у=f(х). В ответе укажите наибольшую из длин этих промежутков.

В3. Для функции у=cosx+sinx+ найдите первообразную, график которой проходит через точку ( ;4).

Запишите решение заданий уровня С с полным обоснованием

С1. Найдите производную функции f(x)=sin(2 ) в точке х =-1 .

С2. Число 24 представьте в виде суммы двух положительных слагаемых, таких, что произведение их квадратов принимает наибольшее значение.

Диагностическая контрольная работа

по алгебре и началам анализа

«Производная функции. Приложения производной»

Вариант 3

Запишите вариант правильного ответа заданий уровня А

А1. На рисунке изображен график функции у=f(x). Укажите число точек экстремумов.

а) 1 б) 2 в) 3 г) 4

А2. Укажите производную функции у= х⁴ - .

а) 4х-

б) 4х3-

в) 4х3+

г) 4х+

А3. Найдите f ' (16), если f(x)=8 -3.

а) 3 б) 2 в) -1 г) 1

А4. Найдите производную функции у=3х²cosx.

а) y'= - 6x sinx б) y'=6xcosx -3x²sinx

в) y'=x³cosx+3x²sinx г) y'=6xcosx+3x²sinx

А5. Найдите минимум функции у=х³-3х+2.

а)-1 б) 0 в) 1 г) 4

А6.Укажите, какая из функций убывает на всей координатной прямой.

а) у=х³+х б) у=х³-х в) у= -х³-х г) у= -х²+1

А7. Найдите производную функции у=(-3+6х)^7.

а) y'=42(-3+6x)⁶ б) y'= -21(-3+6x)⁶ в) y'= 7(-3+6x)⁶ г) y'= -7(-3+6x)⁶

А8.Укажите число точек экстремума функции у=4х-х⁴.

а) 0 б) 1 в) 2 г) 3

А9. Найдите угловой коэффициент касательной, проведенной к графику функции f(x)=4х³-6х²+9 через его точку с абсциссой х₀=1.

а)1 б) 2 в) 0 г) -1

А10. Найдите момент остановки тела, движущегося по закону S(t)=t²-6t-16.

а) 8 б) -2 в) -3 г) 3

А11. Найдите наименьшее значение функции у=2х³-6х на отрезке [0;2].

а) -6 б) -4 в) -2 г) 0.

А12. Найдите тангенс угла наклона касательной, проведенной к графику функции у= - в его точке с абсциссой х₀= -2.

а) 1 б) 2 в) 0 г) -1.

Запишите решение заданий уровня В с полным обоснованием

В1. Найдите значение производной функции f(x)= в точке х₀=2007.

В2. Найдите максимум функции f(x)= .

В3. Напишите уравнение касательной к графику функции f(x)=х²+2х, параллельной прямой у=4х-5. В ответе укажите площадь треугольника, образованного этой касательной и осями координат.

Запишите решение заданий уровня С с полным обоснованием

С1. Рассматриваются всевозможные прямоугольные параллелепипеды, объем каждого из которых равен 32 см³, а одна из боковых граней является квадратом. Найдите среди них параллелепипед с наименьшим периметром основания. В ответе укажите этот периметр.

С2. При каких значениях b прямая у=bx является касательной к параболе

f(x)= х²-2х+4?

Диагностическая контрольная работа

по алгебре и началам анализа

«Производная функции. Приложения производной»

Вариант 4

Запишите вариант правильного ответа заданий уровня А

А1. На рисунке изображен график функции у=f(x). Укажите число промежутков возрастания функции.

а) 1 б) 2 в) 3 г) 0

А2. Укажите производную функции у= 2х³+ .

а) 2х2-

б) 6х2-

в) 6х2+

г) 6х-

А3. Найдите f '(4), если f(x)=4 -5.

а) 3 б) 2 в) -1 г) 1

А4. Найдите производную функции у=(х+3)sinx.

а) y'=(x+3)cosx б) y'=( +3x)cosx в) y'=cosx г) y'=sinx+(x+3)cosx

А5. Найдите точку максимума функции у=х³-3х+2.

а)-1 б) 0 в) 1 г) 4

А6.Укажите, какая из функций возрастает на всей координатной прямой.

а) у=х³+х б) у=х³-х в) у=-х³+х г) у= х²+1

А7. Найдите производную функции у=(4-3х)^5.

а) y'=20(4-3х)⁴ б) y'= 5(4-3х)⁴ в) y'= -15(4-3х)⁴ г) y'= -5(4-3х)⁴

А8.Укажите число точек экстремума функции у= 0,2х⁵- х³.

а) 0 б) 1 в) 2 г) 3

А9. Найдите угловой коэффициент касательной , проведенной к графику функции f(x)= х³-2х+7 в точке с абсциссой х₀=3.

а)7 б) 10 в) 0 г) -1

А10. Найдите момент остановки тела, движущегося по закону S(t)=t²-5t-14.

а) 7 б) -2 в) -2,5 г) 2,5

А11. Найдите наибольшее значение функции у=х³-3х на отрезке [-3;0].

а) -9 б) 4 в) 2 г) 9

А12. Найдите тангенс угла наклона касательной, проведенной к графику функции у = -0,5х² в его точке с абсциссой х₀= -3.

а) -3 б) -4,5 в) 3 г) 0

Запишите решение заданий уровня В с полным обоснованием

В1. Найдите значение производной функции f(x)= в точке х₀=2006.

В2. Найдите минимум функции f(x)= .

В3. Укажите точку графика функции f(x)=х²+4х, в которой касательная параллельна прямой у-2х +5=0. В ответе запишите сумму координат этой точки.

Запишите решение заданий уровня С с полным обоснованием

С1. Рассматриваются всевозможные прямоугольные параллелепипеды, объем каждого из которых равен 4 см ³ , а одна из боковых граней является квадратом. Найдите среди них параллелепипед с наименьшим периметром основания. В ответе укажите этот периметр.

С2. При каком значении а прямая у= -10х+а является касательной к параболе

f(x)=3 х²-4х-2?

Диагностическая контрольная работа

по алгебре и началам анализа

«Производная функции. Приложения производной»

Вариант 5

Запишите вариант правильного ответа заданий уровня А

А1. Укажите производную функции y = sin x – 2x²

а) cos x + 4х б) cos x – 4x в) - cos x – 4x г) - cos x + 4x

A2. найдите производную функции y = 2x³+4x²+2x - 1

а) 6x²+12x+1 б) 6x²+8x+2 в) - 6x²+8x+2 г) 6x²+8x-1

A3. Найдите производную функции y = 1- tg x

а) 1/ cos²x б) - 1/ cos²x в) 1/ sin²x; г) – ctg x

A4. Найдите значение производной функции y = х ⁴(x³-3) в точке с абсциссой x₀= - 1.

а) 13 б) 19 в) – 13 г) – 19

А5. Найдите угловой коэффициент касательной к графику функций

у = 3х + 2cos х в точке с абсциссой x₀= 0.

а) 1 б) 2 в) 3 г) 0

А6. Укажите при каких значения х производная функции

у = (3х² + 1)( 3х² - 1) равна 0

а) ± б) 2 в) ± г) 0

А7. Прямолинейное движение точки описывается законом S = t⁵ – t³ (м). Найдите ее скорость в момент времени t = 2с.

а) 58; б) 68; в) 86; г) 66.

А8. Найдите скорость изменения функции у = 9,5х -3 в произвольной точке х

а) 0

б) 9,5

в)

г) 3

А9. Найдите наименьшее значение функции у = х⁴ - 8х³ + 10х² + 1 на промежутке [1; 6].

а) -124 б) 124 в) 24 г) -144

А10. Укажите промежутки убывания функции

а) ( - ∞; - 1,5)U( -1,5; + ∞) б) ( - ∞; - 1,5)U( 1,5; + ∞)

в) ( - 1,5; -1,5] г) ( - 1,5; -1,5)

А11. Составьте уравнение касательной к графику функции f (x) = x³ в точке с абсциссой x₀= 1

а) у = 3х + 2 б) у = 3х – 4 в) у = 3х – 2; г) у = - 3х + 2.

А12. Найдите все значения х, при которых выполняется неравенство

f`´ (x) ≥ 0, если известно, что f(х) = 6х² – х³

а) ( - ∞; 0]U[ 4; -∞) б) (0; 4] в) (0; 4) г) [0;4]