1. Пусть значения переданных информационных символов (ис) равны

; (19).

Тогда напряжения на входах РУ1 (рис. 1) в момент окончания символьного интервала длительностью будут, соответственно, равны в (11) и (14)

; ;

; .

Используя (14),(18),(19),(6) и (7) получим соответствующие напряжения на входах РУ1

;

;

;

. (20)

При дальнейших преобразованиях интегралов в (20), получим интегралы

и , которые после использования равенства (17) будут равны

; (21)

Получим напряжения на соответствующих входах РУ1 из выражения (20), используя (21).

На 1-м входе ; на 2-м входе ;

на 3-м входе ; на 4-м входе - (22),

где .

Принимая во внимание, что на интервале интегрирования импульс равен 1(В), получим

. (23)

Так как - гауссовская флуктуационная помеха типа белого шума, то из (23) следует, что - гауссовская случайная величина. Вероятностные параметры случайной величины будут определены позднее.

Случайная величина в (22) является причиной ошибок, иногда происходящих в работе РУ1. Чем больше будет дисперсия случайной величины , тем чаще будут происходить ошибки.

При при правильных решениях РУ1 наибольшие напряжения будут формироваться, соответственно, на 1-м, 2-м,3-м или 4-м входах РУ1.

Если значение символа по (19), тогда наибольшее напряжение при правильном решении будет на 1-м входе РУ1 и поэтому будут выполняться три неравенства в соответствии с (22)

> ;

> ;

> . (24), преобразуем (24) к виду

; ; . (25).

После элементарных преобразований из (25) получим

; ; (26),

где - энергия сигнала .

Используя (6), получим .

Имея в виду на интервале интегрирования, и , тогда .

Используя (17), получим .

Окончательно, имеем

(27).

Подставляя (27) в (26), получим

; ; (28).

Если одновременно будут выполняться все три неравенства (28), то РУ1 вынесет правильное решение о том, что в соответствии с (19) значение ИС будет равно .

Если хотя бы одно из неравенств (28) выполняться не будет, тогда демодулятор примет ошибочное решение. На рис. 4 штриховкой обозначены те области на оси , на которых выполняются соответствующие неравенства из системы (28).

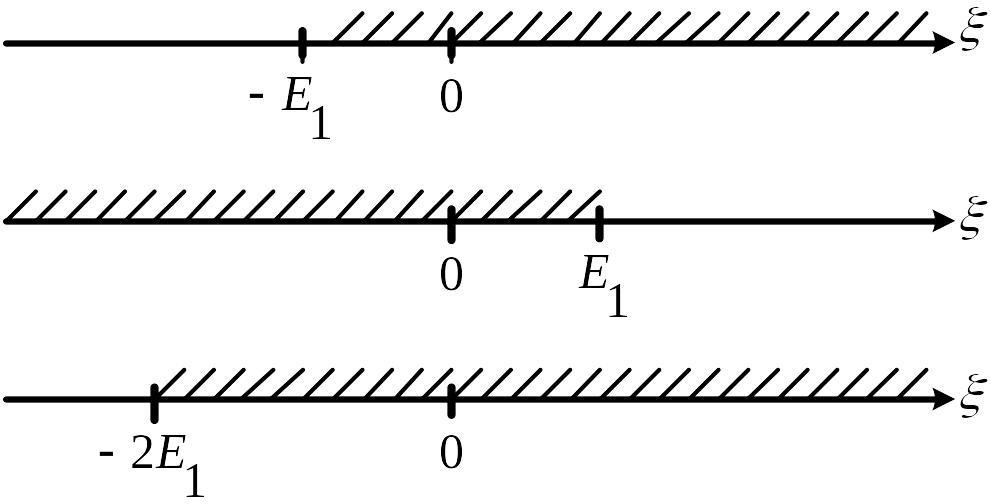
Рис. 4 Интервал , на котором одновременно выполняются неравенства (28).

На рис. 4 определяем, что случайная величина будет удовлетворять неравенству

(29),

если одновременно выполняются три неравенства из (28).

Отсюда следует, что вероятность выполнения неравенства (29) равна вероятности правильного решения , которое принимает РУ1 при передаче значения ИС равного . Вероятность невыполнения неравенства (29) равна вероятности ошибочного решения . Чтобы найти численные значения и , необходимо определить плотность вероятности , которая характеризует случайную величину равной выражению (23). Интегралу (23) соответствует линейный оператор, воздействующий на гауссовский случайный процесс в составе подынтегральной функции. Известно, что воздействие любого линейного оператора на гауссовский процесс сохраняет гауссовское свойство, то есть - гауссовская случайная величина. Поскольку - гауссовская плотность вероятности, то ее характеризуют два параметра – математическое ожидание и дисперсия . Определим эти параметры

(30), Так как математическое ожидание белого шума , а - центрированная случайная величина, поэтому ее дисперсия определяется

. Делаем замену правой частью (23). Получим

, где - корреляционная функция белого шума , то есть ;

- заданная односторонняя спектральная плотность мощности белого шума; - дельта функция.

Таким образом, .

Используя фильтрующее свойство - функции, а также (17) и , получим . Используя (27) будем иметь

(31).

Одномерную плотность вероятности (рис. 5), имея в виду (30) и (31), можно представить в виде

(32).

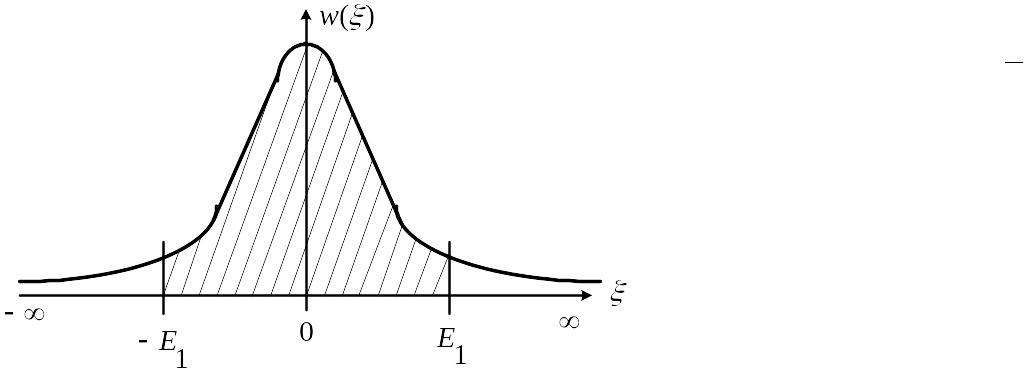
Рис. 5 График , где заштрихованная площадь

есть вероятность правильного решения при значении .

Вероятность правильного решения

= (33),

есть вероятность выполнения неравенства (29) и равна величине заштрихованной площади (рис. 5).

Используя (32), получим = = .

Произведем замену на переменную интегрирования по формуле

, откуда , при , а при .

В результате получим интеграл

(34).

В математических справочниках [6] можно найти специальную функцию, которая называется «интегралом вероятности» или функцией Крампа, ее аргументом является верхний предел интеграла

(35), Эта функция табулирована. Сравним (34) и (35), получим

(36)

Используя (31) можно написать

(37).

Вероятность ошибочного решения, принимаемого РУ1 будет равна

(38).