«П4 к блоку фмс».
На рис 1 изображен блок ФМС. С выхода кодера (К) формируются реализации случайного сигнала (процесса) и поступают на вход блока ФМС. В [7] сигнал, с выхода сверточного кодера, представляет собой случайную последовательность однополярных прямоугольных импульсов с амплитудой 1В и предполагается, что этот сигнал преобразуется в последовательность биполярных прямоугольных импульсов, где
– символ
«1» передается импульсом положительной
полярности с амплитудой
(может быть обозначено
)
и длительностью
,
где
-
бинарный интервал.
-
символ «0» передается импульсом
отрицательной полярности. Параметр
(или
)
может принимать любые значения, например,
.
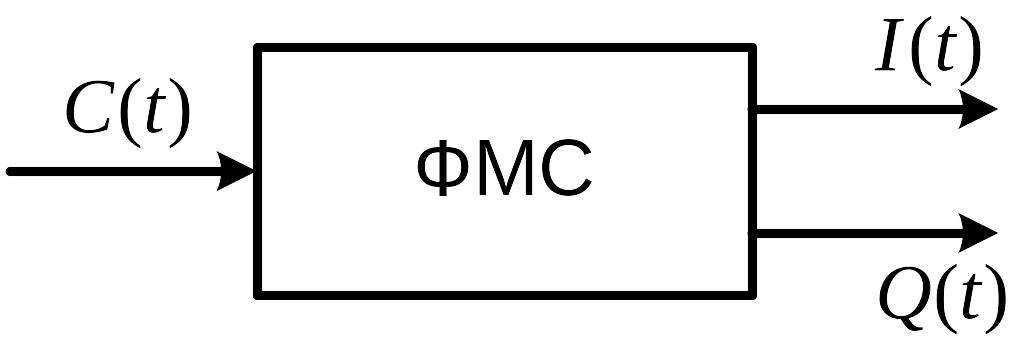
Рис. 1 Формирователь модулирующих символов (ФМС).
Блок ФМС имеет два выхода, на которых формируются выходные
сигналы и .
Фрагмент возможной реализации случайного процесса , соответствующий заданной последовательности двоичных (бинарных) информационных символов - 1 0 1 1 0 , поступающих с выхода кодера (К) представлен на рис. 2б.
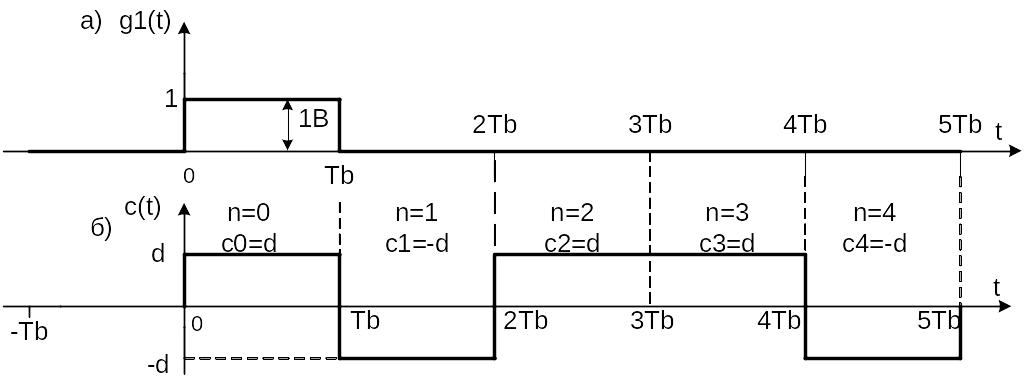
Рис. 2
Импульс
и
фрагмент реализации
.
Реализацию случайного процесса
(1)
можно представить в следующей аналитической форме
(2),
где - прямоугольный импульс длительностью (рис. 2а),
при
(3).
-
прямоугольный импульс такой же формы,
как
,
но сдвинутый вправо относительно
импульса
на величину
,
если
или влево, если
;
-
численный коэффициент, являющийся
реализацией случайной величины
на
- интервале
.
Величина
принимает два дискретных значения
и
с вероятностью 0,5 каждое, то есть
.
Если
в заданной реализации
на
- интервале передается информационный
символ «1», то
,
если передается символ «0», то
(рис. 2б).
Параметр является величиной безразмерной, принимающей заданное численное значение.
Связь
между входным и выходными сигналами
блока ФМС характеризует сигнальное
созвездие для заданного вида модуляции.
Сигнальное созвездие строится в
декартовой системе координат
и
.
Каждой точке (звезде) сигнального
созвездия будут соответствовать
численные значения координат
и
.
Существуют разные формы сигнальных
созвездий, но наибольшее практическое
применение получили созвездия квадратной
формы. Примером таких созвездий являются
КАМ-16, КАМ-64, КФМ-4 и другие, где цифры 16,
64 и 4 показывают количество точек в
созвездии.
Аббревиатура КАМ и КФМ, соответственно, означает - «квадратурная» амплитудная модуляция и «квадратурная» фазовая модуляция *).
Слово
«квадратурная» показывает, что в состав
сигнала КАМ или КФМ входит сумма двух
сигналов, один из которых зависит от
множителя
,
а другой от множителя
.
Благодаря этим множителям сигналы
обладают свойством взаимной ортогональности.
Про такие сигналы говорят, что они
находятся в «квадратуре».
Количество
точек на квадратном созвездии можно
представить в виде
,
где
=2,4,6,8,
- четное число, то есть задать возможные
- битовые блоки или символы.
На каждой координатной оси
и
точкам сигнального созвездия соответствует
возможных амплитуд дискретных координатных
значений (уровней), которые определяются
для каждого значения
из выражения
(4),
где возможное количество бит в - битовом блоке (символе).
--------------------------------------------------------------------------------------------
*) В иностранной литературе виды модуляции КАМ-16, КАМ-64, КФМ4 соответственно, обозначают:
QAM - Quadrature Amplitude Modulation,
QPSK – Quadrature Phase Shift Keying.
Расстояние
между соседними дискретными значениями
равно
,
где
-
заданная величина (в частности может
быть
).
Каждой точке сигнального созвездия
соответствует блок из
двоичных ИС, которые поступают на вход
блока ФМС.
Примеры: