
- •Введение: объект, модель. Модели с одной переменной
- •Основные определения и обозначения
- •Исследование моделей с одной переменной
- •Пусть дано:
- •Этапы качественного исследования дифференциального уравнения
- •Поиск ss
- •Определение типа ss
- •Обозначение поведения системы вне ss
- •Параллели между биологическими и математическими понятиями
- •Физическое описание объекта
- •Множество и система
- •Характеристика системы
- •Эволюция системы
- •Равновесие
- •Абстрактное описание объекта. Фазовое пространство
- •Некоторые базовые математические обозначения
- •Фазовое пространство
- •Инвариантные множества
- •Устойчивость
- •Фазовый портрет
- •Топология
- •Мультистационарные системы
- •Иерархия времен
- •Характерные времена некоторых процессов
- •Модели с иерархией времен
- •Характерные времена в модели
- •Теорема Тихонова
- •Применение
- •Пространственно-распределенные системы
- •Некоторые базовые математические обозначения. Частная производная.
- •Диффузия
- •Уравнение реакции-диффузии
- •Точечная функция
- •Диффузионный член. Уравнение кппf.
Характерные времена в модели
Итак, задача, которую решают при построении
модели, определяет, в частности,
характерное время
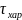 и характерный пространственный масштаб
и характерный пространственный масштаб
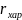 модели.
модели.
Определение
Переменными называют характеристики
объекта, которые меняются за времена
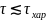 .
.
Определение
Параметрами называют характеристики
объекта, которые меняются за времена
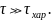
Что же делать с переменными, которые
меняются за
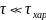 ?
На этот вопрос отвечает теорема
Тихонова.
?
На этот вопрос отвечает теорема
Тихонова.
Определение Быстрые переменные – переменные, меняющиеся за времена много меньшие, чем характерное время, рассматриваемое в модели - .
Определение
Медленные переменные – переменные,
меняющиеся за
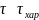 .
.
Теорема Тихонова
Пусть дана модель с двумя переменными
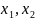 :
:
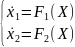
Пусть характерные времена изменения
переменных:
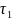 для
для
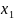 и
и
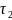 для
для
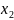 ,
причем
,
причем
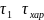 ,
а
,
а
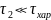 (т.е.
меняется много быстрее, чем интересующие
нас процессы).
(т.е.
меняется много быстрее, чем интересующие
нас процессы).
Построим фазовое пространство (рис.
4-2). На
-изоклинах
скорость изменения одной из переменных
равна нулю. Вне
-изоклин
по условию
меняется много быстрее, чем
(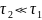 )
если начальное
состояние системы (изображающая точка
)
если начальное
состояние системы (изображающая точка
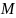 )
лежит вне изоклин, то эволюцию системы
можно условно разделить на две фазы:
)
лежит вне изоклин, то эволюцию системы
можно условно разделить на две фазы:
Быстрое достижение -изоклины за
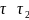 (
(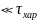 ).
При этом
почти не успевает измениться;
достигает квазистационарного состояния
).
При этом
почти не успевает измениться;
достигает квазистационарного состояния
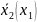 .
.Медленное движение вдоль -изоклины за
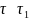 в сторону устойчивого ss. При этом для
любого
«мгновенно» устанавливается
квазистационарное значение
.
в сторону устойчивого ss. При этом для
любого
«мгновенно» устанавливается
квазистационарное значение
.
Рисунок 4-2. Фазовое пространство системы с иерархией времен

Возвращаемся к уравнениям.
означает, что вне изоклин
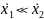
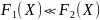 .
.
Определение
Малый параметр - мера отличия
масштабов времени изменения переменных:
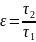 (
(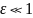 ).
).
Переобозначим:
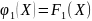 ,
,
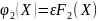 .
Тогда исходная система уравнений примет
вид:
.
Тогда исходная система уравнений примет
вид:
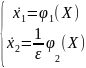 или
или
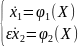
При этом, в отличие от
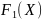 и
и
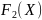 ,
по порядку величины
,
по порядку величины
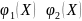 .
Различие в характерных временах изменения
переменных выразилось в малом параметре
.
.
Различие в характерных временах изменения
переменных выразилось в малом параметре
.
Определение Полная система уравнений – исходная система.
Определение Вырожденная система уравнений (здесь - основное уравнение) - подсистема уравнений, не содержащих малый параметр (т.е. с характерными временами изменения переменных порядка ).
Определение Присоединенная система уравнений – подсистема уравнений, содержащих малый параметр (т.е. уравнений для быстрых переменных).
Теорема
При выполнении ряда условий (единственность
решений, непрерывность функций
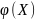 и т.д.)
решение полной системы
уравнений
стремится
к решению системы
и т.д.)
решение полной системы
уравнений
стремится
к решению системы
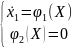 при
при
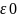 .
Конец
теоремы
.
Конец
теоремы
Это означает, что эволюцию системы допустимо разбить на два этапа (см. рис.4-2) в меру малости :
Достижение изоклины идет не при строго неизменных медленных переменных, а под углом
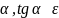 ;
;Движение вдоль изоклины идет не строго по ней, а в ее -полуокресности – с той стороны, куда направлено векторное поле скорости эволюции системы в этой области фазового пространства.
Рисунок 4-3. Фазовое пространство системы с иерархией времен

Применение
В физ.химии и химической кинетике есть ряд методов, разработанных независимо от теоремы Тихонова, но фактически являющихся ее частными следствиями, например:
Модель Михаэлиса–Ментен;
Метод квазистационарных концентраций Боденштейна-Семенова.
