5. Фазовый портрет

Определение Фазовый портрет системы – совокупность всех фазовых траекторий системы.

На практике (это следует из теоремы Коши) для изображения фазового портрета системы достаточно обозначить инвариантные множества и типичные фазовые траектории вне их.

Определение -изоклина – множество точек в фазовом пространстве, в которых .

В частности, наиболее употребима -изоклина – множество точек в фазовом пространстве, в которых .

Системы с несколькими переменными в подавляющем большинстве случаев неинтегрируемы, и их исследование возможно лишь на качественном уровне. При этом принципы качественного исследования системы остаются теми же, что и для систем с одной переменной:

1. Поиск инвариантных множеств. В простейшем случае – поиск ss.

2. Поиск -изоклин – для того чтобы «наметить» общие направления эволюции системы в разных областях фазового пространства и разделить его на бассейны притяжения.

3. Определение типа инвариантных множеств.

4. Построение векторного поля скоростей в фазовом пространстве (Обозначение направления (и, желательно, скорости) эволюции системы вне инвариантных множеств).

6. Топология

Определение Топология - раздел математики, изучающий в самом общем виде явление непрерывности, в частности свойства пространства, которые остаются неизменными при непрерывных деформациях (например, связность, ориентируемость).

В отличие от геометрии, в топологии не рассматриваются метрические свойства объектов (например, расстояние между парой точек).

Основное значение при исследовании любой динамической системы имеет топологическая структура ее фазового портрета (или, что то же, топологическая структура ее векторного поля в фазовом пространстве).

Топологическая структура фазового портрета системы включает в себя наличие и устойчивость инвариантных множеств.

Определение Бифуркация – изменение топологической структуры фазового портрета системы при изменении параметров .

Определение Система структурно устойчива, если топологическая структура ее фазового портрета остается неизменной при «малом шевелении» ее параметров.

Определение Система структурно неустойчива, если «малое шевеление» ее параметров ведет к изменению топологической структуры ее фазового портрета.

4. Мультистационарные системы

In discussion of zero-none genotypic phenomena M. Delbruck proposed in 1949 (Delbruck, 1949) the possibility of bi-stable states in genetic systems. He argued that such situations could be formed based on known physics and chemistry principles. A few years later such phenomena were clearly observed experimentally (Novick and Weiner, 1957). Subsequently an innovative and concrete molecular biological mechanism was proposed and further tested experimentally (Jacob and Monod, 1961). Nowadays there exists an extensive quantitative and predictive study of such genetic switch systems (Zhu et al., 2004, 2007; Ptashne, 2004).

Кауфман

5. Иерархия времен

   1. Характерные времена некоторых процессов

Рисунок 4-1. [из Г.Ю. Ризниченко, 2002]

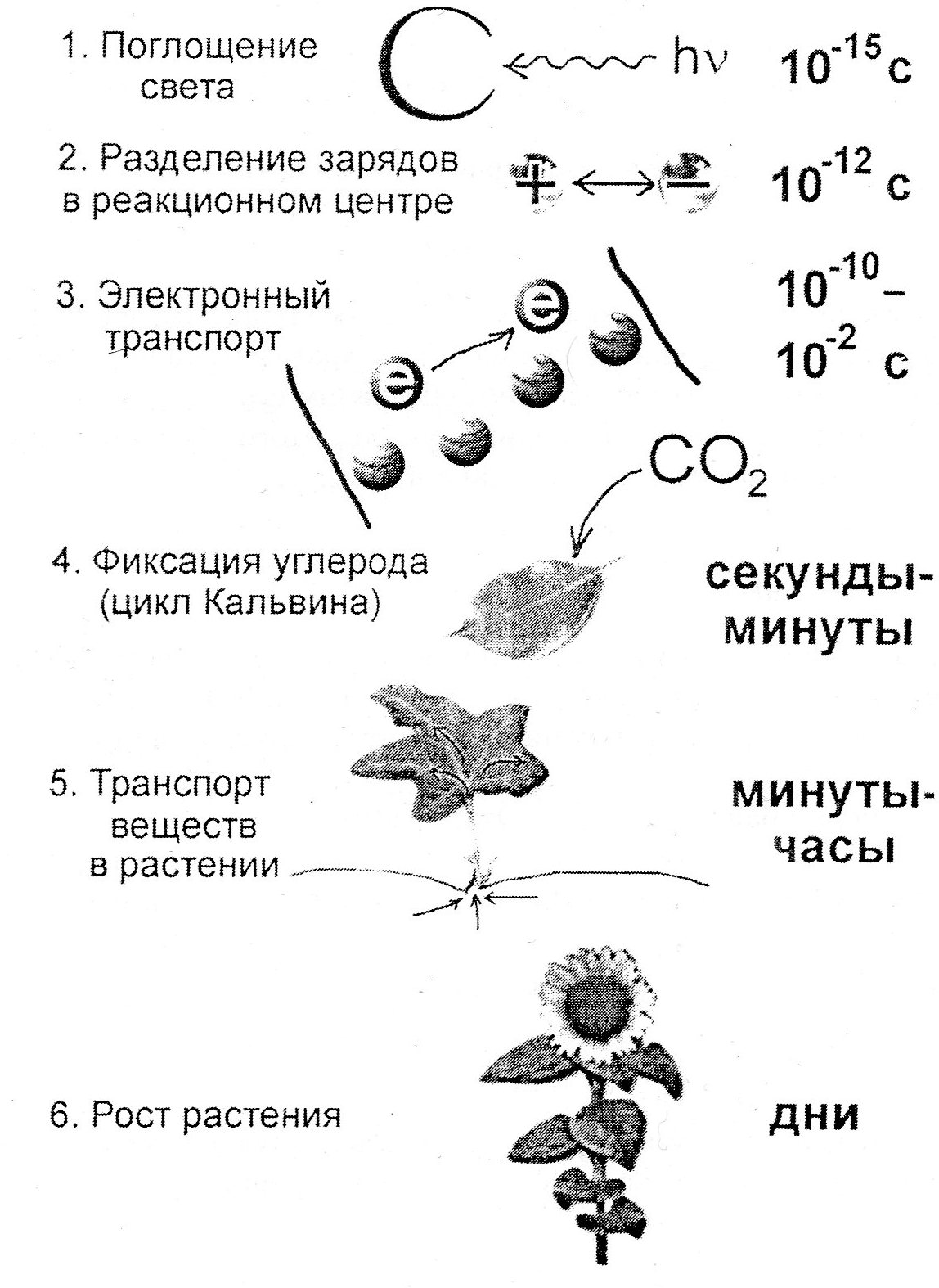
2. Модели с иерархией времен

Не существует идеальных моделей. Любая модель ограничена, основана на допущениях и многое не учитывает. Мало того, чем больше модель учитывает, тем более она сложна и менее решаема. Ценность модели – в способности решить большие задачи малыми средствами.

Ограничения, возникающие при построении любой модели:

1. Выбор системы ( неучет или неполный учет окружения);

2. Выбор характеристик системы, важных для модели ( неучет остальных свойств объекта);

3. Выбор характерного времени – т.е. того временнóго масштаба, в течение которого предполагается наблюдать систему;

4. Выбор характерного пространственного масштаба.