
- •Введение: объект, модель. Модели с одной переменной
- •Основные определения и обозначения
- •Исследование моделей с одной переменной
- •Пусть дано:
- •Этапы качественного исследования дифференциального уравнения
- •Поиск ss
- •Определение типа ss
- •Обозначение поведения системы вне ss
- •Параллели между биологическими и математическими понятиями
- •Физическое описание объекта
- •Множество и система
- •Характеристика системы
- •Эволюция системы
- •Равновесие
- •Абстрактное описание объекта. Фазовое пространство
- •Некоторые базовые математические обозначения
- •Фазовое пространство
- •Инвариантные множества
- •Устойчивость
- •Фазовый портрет
- •Топология
- •Мультистационарные системы
- •Иерархия времен
- •Характерные времена некоторых процессов
- •Модели с иерархией времен
- •Характерные времена в модели
- •Теорема Тихонова
- •Применение
- •Пространственно-распределенные системы
- •Некоторые базовые математические обозначения. Частная производная.
- •Диффузия
- •Уравнение реакции-диффузии
- •Точечная функция
- •Диффузионный член. Уравнение кппf.
Инвариантные множества
Помимо особых точек в фазовом пространстве могут быть и другие специфические множества точек.
Определение Инвариантное множество – ограниченное множество точек, принадлежащее фазовому пространству и отображающееся само на себя в ходе эволюции системы. (Ограниченное множество, из которого изображающая точка не выходит, если она хотя бы раз туда попала).
Типы инвариантных множеств:
Особые точки
Предельные циклы
Определение Предельный цикл – замкнутая фазовая траектория ненулевой длины.
Странные аттракторы – особый тип множеств, инвариантных в неком расширенном смысле, к которому мы вернемся позже.
Устойчивость
Вернемся теперь к понятиям устойчивость/неустойчивость и дадим им определения.
Пусть нас интересует некое (не обязательно
стационарное) состояние системы, которое
мы назовем «стандартным» -
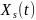 .
.
Определение
Стандартное состояние
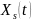 устойчиво по Ляпунову, если
устойчиво по Ляпунову, если
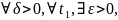 такое что, если только в начальный момент
времени состояние системы
такое что, если только в начальный момент
времени состояние системы
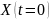 принадлежит
принадлежит
 -окрестности
-окрестности
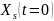 ,
то состояние системы
будет принадлежать
,
то состояние системы
будет принадлежать
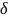 -окрестности
-окрестности
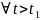 .
.
Рисунок 3-3. Устойчивость стандартного состояния.

Определение
Стандартное состояние
асимптотически устойчиво, если оно
устойчиво по Ляпунову, и при этом
зависит от
,
при чем
 (в пределе
-окрестность
«сужается» до нуля).
(в пределе
-окрестность
«сужается» до нуля).
Определение Стандартное состояние неустойчиво, если оно не является устойчивым по Ляпунову.
В частности, если
 ,
получаем классическое определение
устойчивости стационарных состояний.
,
получаем классическое определение
устойчивости стационарных состояний.
Исторически сложилось, что устойчивость/неустойчивость нестационарных стандартных состояний называется орбитальной.
Понятия устойчивость/неустойчивость можно расширить от стандартных состояний до произвольной области фазового пространства.
Определение -окрестность области - объединение -окрестностей всех точек, принадлежащих .
Определение
Область фазового пространства
устойчива по Ляпунову, если
такое что, если только в начальный момент
времени состояние системы
принадлежит
-окрестности
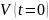 ,
то состояние системы
будет принадлежать
-окрестности
,
то состояние системы
будет принадлежать
-окрестности
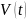 .
.
Аналогично определяются асимптотическая устойчивость и неустойчивость .
Наибольший практический смысл это определение имеет для исследования т.н. странных аттракторов – областей в фазовом пространстве со всюду неустойчивыми фазовыми траекториями внутри них, являющимися инвариантными множествами при рассмотрении их в целом (как области фазового пространства), причем устойчивыми по Ляпунову.
Определение Аттрактор (притягивающее множество) – инвариантное множество, устойчивое по Ляпунову.
Типы аттракторов:
Устойчивые особые точки
Устойчивые предельные циклы
Странные аттракторы
Определение Бассейн притяжения аттрактора – область фазового пространства (диссипативной динамической системы), из которой изображающая точка попадает на аттрактор.
Типы неустойчивых инвариантных множеств:
Неустойчивые особые точки
Неустойчивые предельные циклы
Границы бассейнов притяжения (в том числе сепаратрисы)
