3. Абстрактное описание объекта. Фазовое пространство

   1. Некоторые базовые математические обозначения

Обозначение - множество элементов

Определение Вектор – линейно упорядоченное множество (т.е. множество, в котором каждый элемент имеет свой порядковый номер).

Обозначения: - «вектор-строка»; - «вектор-столбец».

Примеры:

• вектор пространственных координат – упорядоченная тройка чисел ;

• вектор концентраций химических реагентов в однородной системе (где концентрации не зависят от пространственных координат, и каждая из них может быть задана одним числом) – .

Операция Транспонирование вектора – преобразование вектор-столбец  вектор-строка и наоборот.

Обозначение: . , если и наоборот.

Определение Функция векторного аргумента – функция, значение которой зависит от всех компонент вектора : .

Примеры:

• концентрация химического реагента в неоднородной системе, зависящая от пространственных координат – ;

• плотность жидкости в неоднородной среде - .

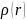Определение Вектор-функция – функция, значениями которой являются векторы: вектор-функция скалярного аргумента .

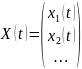Вектор-функция может зависеть от одного или нескольких аргументов – как скалярных, так и векторных.

Примеры:

• вектор-функция скалярного аргумента - пространственное положение частицы в зависимости от времени: , где - пространственные координаты;

• вектор-функция векторного аргумента 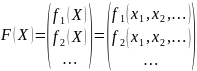- распределение скорости ветра в пространстве (скорость и направление ветра в разных точках пространства): ;

• вектор-функция нескольких аргументов с параметрами - распределение скорости ветра в пространстве в зависимости от времени, при заданных значений температуры и среднего давления: , – параметры.

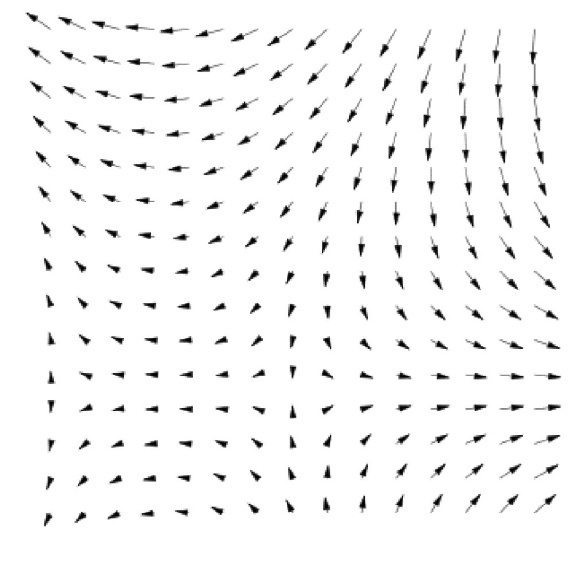
Определение Векторное поле — это отображение (функция), которое каждой точке рассматриваемого пространства ставит в соответствие вектор (эквивалентно вектор-функции векторного аргумента ).

Рисунок 3-1. Векторное поле.

Примеры:

• распределение скорости ветра в пространстве (поле скоростей частиц движущейся среды);

• поле электрической напряженности;

• Векторное поле скоростей автомобилей на Таганской площади.

Операция Дифференцирование вектор-функции – независимое дифференцирование всех ее компонентов: ; .

Пример: если – координаты частицы, то – скорость ее движения (в векторной форме – т.е. с указанием направления).

Запись уравнений эволюции системы

эквивалентна заданию системы дифференциальных уравнений:

2. Фазовое пространство

Пусть «нас интересует» некий объект (система), который, в рамках решаемой задачи, однозначно описывается вектором переменных 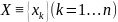и вектором параметров .

Состояние системы при заданном однозначно задается вектором значений .

Построим пространство , где по k-й оси будем откладывать значение k-й переменной 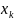(k-й компоненты ). Т.к. переменных n, пространство получится n-мерное. Состояние системы (при заданном ) будет (взаимно однозначно) соответствовать точке в этом пространстве. Такое пространство называют фазовым.

Определение Фазовое пространство – пространство, на котором представлено множество всех состояний системы, так, что каждому возможному состоянию системы соответствует точка фазового пространства.

Определение Изображающая точка – точка в фазовом пространстве, соответствующая состоянию системы в данный (любой) момент времени.

Определение Фазовая траектория – множество изображающих точек в последовательные моменты времени в течение всего времени эволюции системы (траектория движения изображающей точки в фазовом пространстве, соответствующая эволюции системы).

Рисунок 3-2. Фазовое пространство для системы с двумя переменными . 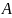– изображающая точка.

Определение Особые точки (неподвижные точки) – точки в фазовом пространстве, в которых 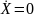(т.е. ).

Определение Регулярные точки – точки в фазовом пространстве, в которых не все .

Важнейшую роль в теории дифференциальных уравнений играет т.н. теорема Коши о существовании и единственности решения:

Теорема Для системы уравнений

при достаточно мягких условиях на вид функций

существует единственное решение в период 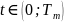, если начальное состояние системы соответствует регулярной точке.

(Максимальный «отрезок времени» в течение которого это выполняется - - определяется видом ).

Теорема Коши автоматически исключает пересечение фазовых траекторий в любой регулярной точке. Конец теоремы