
- •Введение: объект, модель. Модели с одной переменной
- •Основные определения и обозначения
- •Исследование моделей с одной переменной
- •Пусть дано:
- •Этапы качественного исследования дифференциального уравнения
- •Поиск ss
- •Определение типа ss
- •Обозначение поведения системы вне ss
- •Параллели между биологическими и математическими понятиями
- •Физическое описание объекта
- •Множество и система
- •Характеристика системы
- •Эволюция системы
- •Равновесие
- •Абстрактное описание объекта. Фазовое пространство
- •Некоторые базовые математические обозначения
- •Фазовое пространство
- •Инвариантные множества
- •Устойчивость
- •Фазовый портрет
- •Топология
- •Мультистационарные системы
- •Иерархия времен
- •Характерные времена некоторых процессов
- •Модели с иерархией времен
- •Характерные времена в модели
- •Теорема Тихонова
- •Применение
- •Пространственно-распределенные системы
- •Некоторые базовые математические обозначения. Частная производная.
- •Диффузия
- •Уравнение реакции-диффузии
- •Точечная функция
- •Диффузионный член. Уравнение кппf.
Характеристика системы
Определение свойств объекта, интересующих нас в данном случае (например: в задаче о расширении газа важно знать p, V, T, теплоемкость, но неважны положения отдельных молекул газа).
Введение меры - количественное выражение этих свойств (любое свойство любого объекта доступно для объективного исследования только если его можно выразить количественно).
Определение Переменные - свойства объекта, меняющиеся за период наблюдения.
Определение Параметры - свойства объекта, не меняющиеся за период наблюдения или меняющиеся пренебрежимо мало.
Предварительные обозначения
- множество переменных системы,
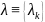 - множество параметров системы.
- множество параметров системы.
 и
однозначно описывают объект (в рамках
используемой модели / подхода).
и
однозначно описывают объект (в рамках
используемой модели / подхода).
Определение Состоянием объекта назовем полную (в рамках используемого подхода) совокупность его свойств ( и ).
Состояние объекта меняется во времени, и задача max для исследователя – понять причины этой эволюции и предсказать ее.
Эволюция системы
Для предсказания эволюции системы
строят математические модели. Конечная
цель любой модели – получить в явном
виде зависимость
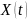 при заданном
.
Модель может строиться с использованием
различных математических подходов.
при заданном
.
Модель может строиться с использованием
различных математических подходов.
Нас будут интересовать модели с использованием дифференциальных уравнений – уравнений эволюции системы.
Предварительное обозначение Общий вид уравнений эволюции для произвольной системы:
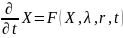
Здесь
– переменные системы,
- параметры,
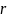 – вектор пространственных координат,
– вектор пространственных координат,
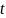 - время
- время
Модели (вне зависимости от математического подхода) могут быть условно двух типов:
Описательные – вид
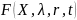 получают «подгонкой» под эмпирические
результаты
получают «подгонкой» под эмпирические
результатыТеоретические - вид - логическое следствие неких общих базовых принципов
Механика
Механический подход предполагает распознавание «истинной» природы изменения системы – законов взаимодействия «элементарных» частиц материи.
Рассмотрим механическую систему из N частиц (материальных точек).
Переменные:
 (координаты частиц),
(координаты частиц),
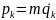 (импульсы),
(импульсы),
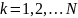 (если импульсы и координаты даны в
векторной форме), или
(если импульсы и координаты даны в
векторной форме), или
 (если импульсы и координаты даны по
компонентам).
(если импульсы и координаты даны по
компонентам).
Законы эволюции системы – законы Ньютона:

(Для простоты оставлены только гравитационные взаимодействия).
Интегрируя эти уравнения и зная начальные
условия –
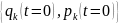 ,
можно вычислить
,
можно вычислить
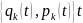 ,
т.е. как прошлое, так и будущее системы.
Т.о. эволюция механической системы
полностью детерминирована и однозначно
определена как в прошлом, так и в будущем.
,
т.е. как прошлое, так и будущее системы.
Т.о. эволюция механической системы
полностью детерминирована и однозначно
определена как в прошлом, так и в будущем.
Кинетика
Почти все реальные системы состоят из
огромного числа частиц (12 г углерода
содержат
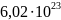 атомов в такой
системе
атомов в такой
системе
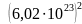 парных взаимодействий
парных взаимодействий
 ).
Очевидно, поиск индивидуальных траекторий
частиц невозможен (даже в классическом
- неквантовом – подходе). Поэтому для
описания реальных систем приходится
вводить усредненные статистические
характеристики системы:
).
Очевидно, поиск индивидуальных траекторий
частиц невозможен (даже в классическом
- неквантовом – подходе). Поэтому для
описания реальных систем приходится
вводить усредненные статистические
характеристики системы:
Переменные –
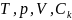 (концентрация различных веществ) и т.д.
(концентрация различных веществ) и т.д.
Параметры – теплоемкость, химическое сродство, константы скорости реакций, константы диффузии и т.д.
Уравнения эволюции для такой системы основаны не на фундаментальных физических взаимодействиях, а на эмпирических или статистических закономерностях:
Закон действующих масс
Уравнение теплопроводности
Уравнение диффузии
и т.д.
Термодинамика
В рамках термодинамического подхода систему также описывают с помощью интегральных и статистических величин. Принципиальное отличие от кинетического подхода – в использовании т.н. функций состояния, которые позволяют, несмотря на статистический подход, пользоваться фундаментальными физическими принципами.
Определение Функцией состояния системы назовем любую функцию, заданную на множестве возможных состояний системы и однозначно определяемую для любого состояния ( функция состояния зависит только от текущего состояния системы, но не от ее истории).
Функции состояния
Энергия E – способность системы совершать работу. Одна из наиболее фундаментальных физических величин. Не только однозначно определяется для любого состояния системы, но и в значительной степени определяет ее эволюцию.
Примеры:
Классическая механика:
 (H – гамильтониан – оператор
полной энергии)
(H – гамильтониан – оператор
полной энергии)Квантовая механика:
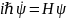 (
( – гамильтониан,
– гамильтониан,
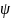 – волновая функция)
– волновая функция)
Первое начало термодинамики:
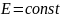 – закон сохранения энергии
– закон сохранения энергии
Энтропия S Мы рассмотрим только статистическое (больцмановское) определение энтропии:

Здесь
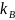 – константа Больцмана,
– константа Больцмана,
 – число микросостояний, соответствующих
данному макросостоянию системы).
– число микросостояний, соответствующих
данному макросостоянию системы).
Определение Микросостояние системы – состояние системы, полностью определенное на языке механики, т.е. задаваемое всей совокупностью механических переменных (импульсами и координатами всех частиц).
Для реальной системы невозможно определить ее микросостояние (в квантовой механике это вообще строго запрещено).
Определение Макросостояние системы – состояние системы, задаваемое совокупностью используемых макроскопических (статистических) переменных ( и т.д.).
Любое макросостояние может быть реализовано большим количеством микросостояний.
В статистическом смысле S – «вероятность» данного макросостояния.
Второе начало термодинамики:
 (для изолированной системы)
Система
не может спонтанно перейти в менее
вероятное макросостояние без взаимодействия
с окружающей средой.
(для изолированной системы)
Система
не может спонтанно перейти в менее
вероятное макросостояние без взаимодействия
с окружающей средой.
