1. Введение: объект, модель. Модели с одной переменной

   1. Основные определения и обозначения

Логические обозначения

– следовательно

– равносильно

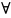– каждый, для каждого, для всех

– существует

Переменные, параметры

Определение Переменные - свойства объекта, меняющиеся за период наблюдения.

Определение Параметры - свойства объекта, не меняющиеся за период наблюдения или меняющиеся пренебрежимо мало.

Обозначения

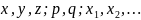– переменные

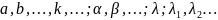– параметры

Изменение переменных

– время; характерные времена протекания каких-либо процессов (изменения переменных)

– скорость изменения (производная по времени)

– ускорение изменения (вторая производная по времени)

Определение Уравнение эволюции – математически выраженная закономерность изменения переменной величины:

или ( – переменная, 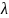– параметр)

Стационарные состояния

Определение Стационарное состояние – состояние объекта (системы), в котором переменные остаются неизменными: ( )

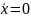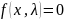Обозначения

ss = stationary state – стационарное состояние

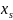(или , или ) – стационарное значение

Определение Флуктуация – отклонение значения переменной от заданного (выбранного) значения

На практике флуктуациями называют небольшие случайные отклонения, шум.

В реальных системах флуктуации постоянно существуют за счет неконтролируемых взаимодействий.

В моделях флуктуации используют для «тестирования» стационарных (или нестационарных, но заранее выбранных) состояний системы на предмет их «стабильности» (устойчивости): придают переменной некоторое отклонение и смотрят, вернётся ли она в исходное состояние.

Предварительные определения

ss устойчиво по Ляпунову – если возникшие (наложенные извне) флуктуации со временем не увеличиваются (состояние системы остается в некой окрестности исходного)

ss асимптотически устойчиво – если возникшие (наложенные извне) флуктуации со временем «затихают» (система в точности возвращается в исходное состояние)

ss неустойчиво – если возникшие (наложенные извне) флуктуации со временем возрастают (в результате незначительной начальной флуктуации система теряет исходное стационарное состояние и переходит в новое состояние)

2. Исследование моделей с одной переменной

   1. Пусть дано:

• Система (объект) с одной переменной и одним параметром (или набором параметров)

• Уравнение эволюции:

Цель любого исследования системы – выяснить, как будет меняться с течением времени в зависимости от наперед заданного значения (т.е. получить в явном виде ).

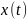В простых моделях эта цель достигается прямым интегрированием:  

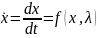
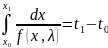
Но большинство систем настолько сложны, что выразить через элементарные функции ( и др.) нельзя. Такие системы называются неинтегрируемыми (невозможно напрямую посчитать ). Их либо решают приблизительно, либо решают на компьютере. Но часто, чтобы понять, как «в общем» будет вести себя , их исследуют с помощью качественной теории дифференциальных уравнений.

2. Этапы качественного исследования дифференциального уравнения

1. Поиск ss



Решаем алгебраическое уравнение

2. Определение типа ss

Задаем флуктуацию :



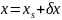
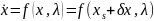
Смотрим знак :

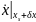если при начальном отклонении 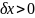начнет убывать ( 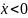), и наоборот – устойчиво,

если при начальном отклонении продолжит возрастать ( ), и наоборот – неустойчиво:

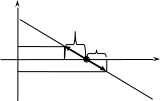
Рисунок 1-1.

Если: при при  ss устойчиво (асиптотически)
Если: при при  ss неустойчиво

Итак, условия устойчивости ss для системы с одной переменной:

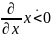(убывание функции 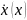) – ss устойчиво

(возрастание функции ) – ss неустойчиво

Рисунок 1-2. Обозначения:

ss устойчиво (асиптотически)
ss неустойчиво