Реализация блока перевода в код с избытком 3.
Последние 4 бита результата представить в коде с избытком 3.
Коды с избытком 3 - это коды чисел из системы ( 8421 + 3 ). В этом коде каждая десятичная цифра ai представляется в виде двоичного эквивалента суммы ai+3. В отличие от кода 8421 код 8421+3 – самодополняющийся, но не имеющий свойства взвешенности. Таким образом, нам необходимо сначала представить последние 4 бита результата в двоично-десятичном коде, а затем прибавить к полученным битам 3.
Максимальное число, которое может быть подано на дешифратор в дополнительный код будет:
(1111) 2 = (15)10
Принцип работы устройства следующий: первые 9 чисел в двоичной кодировке совпадают с кодировкой двоично-десятичной, от остальных значений(до 15, т.к. 4 бита) необходимо отнять 10 и перевести остаток в двоичный код.
Число |
x |
y |
||||||
|
X4 |
X3 |
X2 |
X1 |
Y4 |
Y3 |
Y2 |
Y1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
2 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
3 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
4 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
5 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
6 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
7 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
8 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
9 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
10 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
11 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
12 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
13 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
14 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
15 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
Табл. 4.3 таблица истинности для двоично- десятичного кода
В этой таблице каждую из переменных Yi можно рассматривать функцией коэффициентов x1,x2,x3,x4 двоичного кода и составить карты Карно для 4-х переменных. Составим для каждой функции Yi карты Карно.
Для Y4:
Для Y3:
X3x4 |
X1x2 |
|||
OO |
1O |
11 |
O1 |
|
OO |
0 |
0 |
0 |
0 |
1O |
1 |
1 |
1 |
1 |
11 |
0 |
0 |
1 |
1 |
O1 |
0 |
0 |
0 |
0 |
Для Y2:
X3x4 |
X1x2 |
|||
OO |
1O |
11 |
O1 |
|
OO |
0 |
0 |
1 |
1 |
1O |
0 |
0 |
1 |
1 |
11 |
1 |
1 |
0 |
0 |
O1 |
0 |
0 |
0 |
0 |
X3x4 |
X1x2 |
|||
OO |
1O |
11 |
O1 |
|
OO |
0 |
1 |
1 |
0 |
1O |
0 |
1 |
1 |
0 |
11 |
0 |
1 |
1 |
0 |
O1 |
0 |
1 |
1 |
0 |
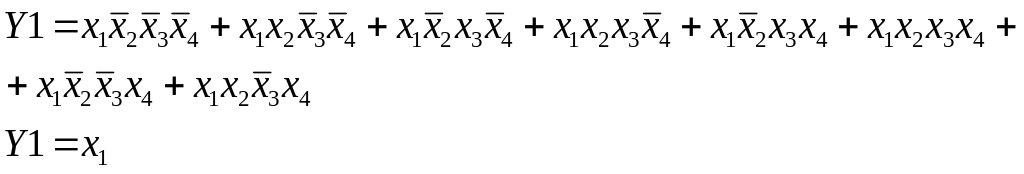
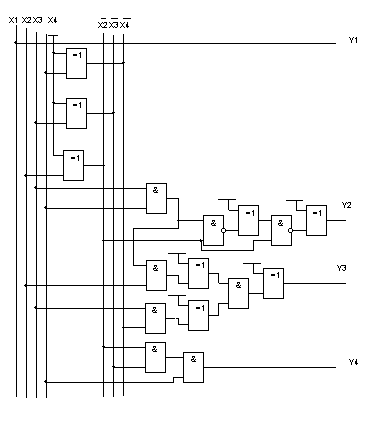
Рис. 4.28 схема перевода в двоично-десятичный код
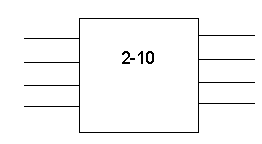
Рис. 4.29 условное обозначение дешифратора перевода в двоично-десятичный код