19.3. Дифференцируемость функции комплексной переменной.
19.3.1.
Определение производной. Аналитичность
ФКП. Пусть
определена, однозначна и принимает
собственные значения в окрестности
точки
.
Производной функции
в точке
называется
предел
.
Функция, имеющая конечную производную
в точке
,
называется дифференцируемой в этой
точке.
В
этом определении важно, что стремление
может проходить по любому пути. Как мы
увидим дальше, вследствие этого
обстоятельства существование производной
не сводится к существованию частных
производных функций
и
,
а требует некоторых дополнительных
условий. Сейчас мы дадим определение
основного в теории ФКП понятия -
аналитичности
функции в
точке и в области.
Определение. Однозначная функция называется аналитической (регулярной, голоморфной) в точке , если она дифференцируема в некоторой окрестности этой точки.
Однозначная функция называется аналитической в области D, если она аналитична в каждой точке этой области.
Примеры.
1.
.
В этом случае
.
Таким образом
, эта функция дифференцируема в любой
точке, и её производная равна 2z.
2.
Докажем, что
эта функция не имеет производной ни в
какой точке
.
Будем стремить
по двум путям: по прямой, параллельной
действительной оси Ох
(в этом случае
),
и по прямой, параллельной мнимой оси Оу
(в этом случае
).
В первом случае
,
во втором
.
Эти пределы равны, только если
.
Таким образом, функция
может быть
дифференцируема в единственной точке
,
во всех остальных точках пределы
различны в зависимости от способа
стремления
,
т.е.
не существует.
19.3.2. Условия Коши-Римана (Даламбера-Эйлера).Сейчас мы сформулируем и докажем важнейшую в теории ФКП теорему о необходимых и достаточных условиях дифференцируемости (а, следовательно, аналитичности) функции.
Для
того, чтобы функция
была дифференцируема в точке
,
необходимо и достаточно, чтобы функции
и
были дифференцируемы в точке (х,у),
и чтобы в этой точке выполнялись
соотношения
.
Доказательство.
Необходимость.
Здесь мы применим идею, которой
воспользовались, когда доказывали, что
функция
не имеет
производных в точках
:
подойдём к точке z
двумя путями - по направлениям
(
)
и
(
).
В
первом случае:
.
Во
втором случае: (напомню, что
)
.
Пределы должны быть равны, поэтому
.
Достаточность.
По предположению теоремы, функции
дифференцируемы в точке (х,у),
поэтому
где
,
- бесконечно малые
более высокого порядка по сравнению с
,
т.е.
,
.
Найдём
.
.
Последнее
слагаемое - бесконечно малая высшего
порядка по сравнению с
:
;
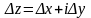далее, в предыдущих слагаемых, пользуясь
формулами Коши-Римана, оставим только
частные производные по х,
т.е. заменим
на
,
на
;
тогда
.
Отсюда следует, что существует
,
т.е. функция дифференцируема в точке
(х,у).
Производная
дифференцируемой функции может находиться
по любой из формул
,
эти равенства следуют из условий
Коши-Римана. При вычислении производных
можно пользоваться всеми правилами
действительного анализа:
(в точках, где
.