Санкт-Петербургский Государственный Университет

Математико-Механический факультет

иванов иван иванович

РЕФЕРАТ

Разработка Программы минимизации конечного абстрактного автомата по алгоритму бржозовского

Кафедра <кафедра>

Группа №

ХХ.БХХ-мм

Преподаватель: Федорченко Л.Н.

доцент кафедры информатики

Санкт-Петербург 2019

Введение

Может быть поставлен такой вопрос: нельзя ли для произвольного конечного автомата построить эквивалентный конечный автомат с меньшим числом состояний? Оказывается, что ответ на этот вопрос положителен. Более того, можно построить конечный автомат, эквивалентный исходному и имеющий наименьшее число состояний (среди всех конечных автоматов, эквивалентных ему). Процедуру построения такого автомата называют минимизацией конечного автомата.

Среди прочих алгоритмов минимизации алгоритм от Бржозовского (Janusz A. (John) Brzozowski) выделяется, по крайней мере, следующими качествами:

1. Он элегантен и весьма оригинален.

2. Он эффективен.

3. Он работает даже с недетерминированными конечными автоматами.

Постановка задачи

Дан конечный автомат. Конечным автоматом (КА) будем называть формальную систему: 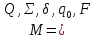), где

Q — это конечное непустое множество состояний,

𝛴 — это входной алфавит,

𝛿 — это отображение типа ,

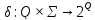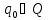— начальное состояние,

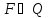— это множество заключительных состояний.

Найти конечный автомат, эквивалентный исходному и имеющий наименьшее число состояний (среди всех конечных автоматов, эквивалентных ему.

Описание алгоритма

Обладая обычными процедурами обращения (rev) и детерминизации (det) конечного автомата, мы, с помощью идеи Бржозовского, можем немедленно приступить к минимизации заданного автомата. Для этого надо дважды провести его через обе вышеуказанные процедуры:

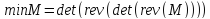, где

M это исходный конечный автомат,

rev это процедура обращения КА,

det это процедура детерминизации КА,

minM это минимизированный КА.

Строгое доказательство того, что этот алгоритм работает, содержится в [Bru], [JMC]. Интуитивно можно попытаться представить себе, как операции det(rev(…)) объединяют неразличимые состояния в обоих направлениях. В реализации алгоритма было использовано “ленивое вычисление” подмножеств без “дьявольских состояний” [Джо] в качестве процедуры детерминизации.

Описание программы

Представление данных

Программа написана на языке программирования Python 3.

Массив fa представляет из себя конечный автомат, который будет минимизирован.

К примеру:

fa[Q] = [0, 1, 2, 3] означает, что у автомата всего четыре состояния,

fa[𝛴] = ['a', 'b'] представляет из себя входной алфавит,

fa[𝛿] = [[[1, 2], [2]], [[2], [3]], [[1, 2], [3]], [[], []]] каждый подмассив является представлением перехода конечного автомата,

fa[q₀] = [0] и fa[F] = [3] множества начальных и конечных состояний.

На выходе программа выдаёт файл с расширение .gv, которая позволяет удобно рассмотреть полученный граф в графическом формате .svg.

Основные классы или функции в программе

Программа состоит из четырёх основных функций:

1. def fa_rev(fa) представляет из себя операцию обращения конечного автомат;

2. def fa_det(fa) представляет из себя операцию детерминизации конечного автомата;

3. def fa_gv(fa, filename) вспомогательная функция, которая выводит данный конечный автомат в виде графа в файл;

4. def fa_min(fa):

return fa_det(fa_rev(fa_det(fa_rev(fa)))) собственно сама функция алгоритма Бржозовского

Результат

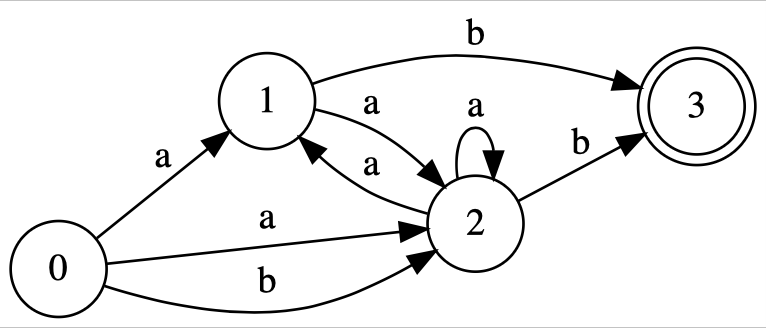
Для начального графа, имеющего такой вид:

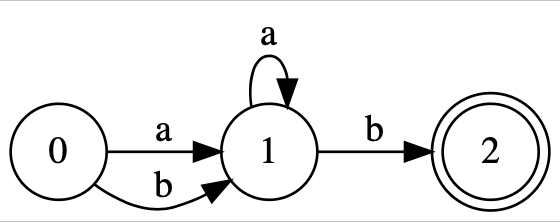
Результат минмизации алгоритмом Бржозовского будет таковым:

Заключение

Самым эффективным алгоритмом минимизации принято считать алгоритм Хопкрофта, который, как и прочие традиционные алгоритмы, работает только с ДКА. Его асимптотическое время выполнения зависит от логарифма исходных данных. С другой стороны очевидно, что алгоритм Бржозовского в худшем случае будет обладать экспоненциальным временем выполнения, ведь этого требует процедура детерминизации, выполняемая дважды. На практике же наблюдается парадокс, алгоритм Бржозовского во многих случаях опережает прочие подходы к минимизации, включая и алгоритм Хопкрофта.

Список литературы

Bru: , [1],

JMC: , [2],

Джо: , [3],

[1]	B. W. Watson, «A taxonomy of finite automata minimization,» [В Интернете]. Available: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.55.8900.
[2]	A. K. T. P. J.-M. Champarnaud, «Split and join for minimizing: Brzozowski's algorithm,» [В Интернете]. Available: https://cs.stackexchange.com/questions/105574/proof-of-brzozowskis-algorithm-for-dfa-minimization.
[3]	Р. М. Д. У. Джон Хопкрофт, Введение в теорию автоматов, языков и вычислений. Второе издание, Издательство “Вильямс”.