Эквивалентная ставка дисконта, доходность векселя
Ставка дисконта представляет собой характеристику доходности векселя. Однако она не позволяет непосредственно сравнить доходность векселя с доходностью других ценных бумаг, так как, во-первых, она рассчитывается на базе 360 дней, и, во-вторых, при ее определении скидка относится к номиналу, тогда как реально покупатель инвестирует меньшую сумму, а именно, цену. Данные обстоятельства занижают доходность векселя. Поэтому необходимо определить формулу для пересчета ставки дисконта в доходность на базе 365 дней и учета цены. Ее можно найти из следующего равенства:
где: r – эквивалентная ставка доходности.
Тогда
|
(2.61) |
Пример 2.25. Ставка дисконта равна 20%, срок погашения наступает через 30 дней. Определить эквивалентную ставку. Она равна:
или
20,6%.
Эквивалентную ставку также можно определить из формулы 2.60, если взять финансовый год равным 365 дням:
|
(2.62) |
2.3. 2. Процентный вексель Определение суммы начисленных процентов и вексельной суммы
По процентному векселю начисляются проценты по ставке, которая указывается в векселе. Сумму начисленных процентов можно определить по формуле:
|
(2.63) |
где I – сумма начисленных процентов; N – номинал векселя; С% – процентная ставка, начисляемая по векселю; tS – количество дней от начала начисления процента до его погашения.
Пример 2.26.
Номинал векселя равен 1 млн. руб., по векселю начисляются 12% годовых, с начала начисления процентов до момента предъявления векселя к оплате прошло 30 дней. Определить сумму начисленных процентов.
Она равна:
руб.
Общая сумма, которую держатель процентного векселя получит при его погашении, равна сумме начисленных процентов и номинала. Ее можно определить по формуле:
|
(2.64) |
где: S – сумма процентов и номинала векселя.
Определение цены векселя
Цена векселя определяется по формуле:
|
(2.65) |
где Р – цена векселя; t – количество дней от покупки до погашения векселя; r – доходность, которую желал бы обеспечить себе инвестор.
Определение доходности векселя
Доходность векселя определяется по формуле:
|
(2.66) |
Пример 2.27.
Номинал векселя 1 млн. руб., по векселю начисляется 15% годовых, период с момента начала начисления процентов до погашения бумаги равен 60 дням. Определить доходность операции для инвестора, если он купит вексель за 30 дней до погашения по цене 1010 тыс. руб. и предъявит его по истечении этого срока.
Доходность равна:
или
17,82%.
Формулы определения цены и доходности векселей были представлены без учета налогообложения. Корректировать формулы на налоговые ставки следует таким же образом, как было показано в примерах с облигациями, т. е. необходимо умножить суммы, подлежащие налогообложению, на (1 – Tax). Например, для процентного векселя налоги взимаются с суммы начисленных процентов. Поэтому корректировке подлежит величина:
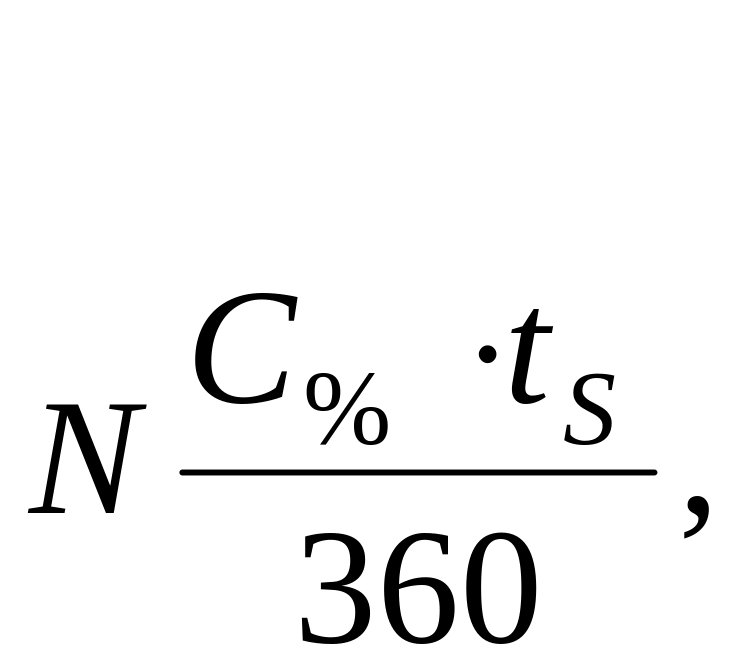
а именно:
